S Y N O P S I S O
F
T H E S I S W O R
K
This manuscript describes the
research for which I won the first prize in the 1999
Outstanding Thesis Competition of American Physical Society,
Division of Atomic, Molecular and Optical Physics.
The first prize was shared between myself and Brett Esry.
More information on
the prize, and a short abstract can be found
here.
To find out more about the other finalists in
that competition, take a look at the abstracts of the special
session in Atlanta for the DAMOP
Outstanding Thesis Award.
The participants were
Michael Andrews (MIT), advisor: Wolfgang Ketterle
Brett Esry (JILA Colorado), advisor: Chris Greene
Lisa Wiese (Nebraska), advisor: Duane Jaecks
Fredrick Fatemi (Virginia), advisor: Louis Bloomfield
Jens Nöckel (Yale), advisor: Douglas Stone.
The
Award Committee consisted of:
Hossein Sadeghpour ITAMP, Harvard University
Eric Cornell, JILA
Wendell Hill , University of Maryland
Barbara Levi, American Institute of Physics
Michael Morrison, University of Oklahoma
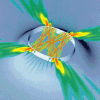
Taken to the extreme, total internal reflection makes it
possible to fabricate lasers with resonator dimensions on the
order of the optical wavelength [2,5]. In particular,
ultralow-threshold lasing without the need for Bragg mirrors
has been observed in thin semiconductor disk resonators with a
circular cross section. These microdisk lasers rely on
ring-shaped modes localized near the dielectric interface with
the surrounding lower-index medium (e.g. air). In the ray
picture, the light circulates around the disk in a series of
total internal reflections (see Fig. 1), forming a
trajectory that is known from acoustics as a
``whispering-gallery'' (WG) pattern.
For the analogous WG modes in fused-silica microspheres,
record Q-factors well above 109 have been measured
at optical wavelengths [6,7]. Infinite lifetimes are unattainable
even in the absence of material losses, because total internal
reflection is frustrated by the finite curvature of the
surface. This unavoidable outcoupling loss is analogous to
quantum tunneling and its rate is correspondingly small. The
discrete wavelengths at which WG resonances occur in thin disks
or perfect spheres, as well as the associated linewidths, can
be calculated straightforwardly because for a rotationally
symmetric cross section, the conservation of angular momentum
(L) renders Maxwell's wave equations separable [8,9]. Besides
microlasers with different active materials [10,11], there is a
wide range of other applications that can benefit from the
long-lived (metastable) states in such dielectric resonators
[12,13].
In most of these applications, however, rotationally
symmetric microcavites have a shortcoming: they lack a
preferred emission direction, and the coupling between the
resonator and adjacent optical devices (such as fibers) poses
major technical challenges, requiring accurate placement of
coupling components in the exponentially decaying nearfield of
the resonator [7,12]. While it seems clear that rotational
symmetry should be broken to achieve directionality, it is far
from obvious how to chose the proper deformation. This is
because the wave equation is not separable when no good quantum
numbers such as angular momentum are preserved, and a typical
mode then contains admixtures of many different L.
One way to explore the modes of asymmetric dielectric
resonators are exact solutions of the wave equation. We have
carried out such calculations for dielectric microcylinders (or
disks) [14] at deformations well beyond the
reach of a shape perturbation theory [15,16] that had been
previously applied to microdroplets. However, in order to
decide for which shapes it is worthwhile to perform numerical
or real experiments in the first place, and what phenomena to
expect, we resort to the explanatory and predictive power of
the ray picture.
A nonseparable wave equation means that rays move along
chaotic trajectories. One therefore has to address the
implications of chaotic ray dynamics for the wave solutions: a
typical question in the field of quantum chaos [17]. This defines our agenda: Analyze the
ray dynamics of asymmetric resonant cavities in order to draw
conclusions about the intrinsic emission properties of the
individual metastable states under consideration, i. e.,
their lifetimes and emission directionality. This requires
semiclassical methods to connect resonances with rays.
Semiclassical quantization of course yields the resonance
frequencies, too - this has historically been its main
objective [17,18,19,20].
Semiclassical theory for the lifetimes of
metastable states has received strong impulses from chemical
physics, in particular from the study of reactive collisions
[20,21,22,23]. Completely regular
(i.e., non-chaotic) systems can be semiclassically quantized
using some version of the WKB or EBK approximation [18,19]; for fully
chaotic systems, spectrum and lifetimes can be obtained from
the periodic-orbit theory pioneered by Gutzwiller [17,23]. The deformed
dielectric resonator, however, generically belongs to the far
larger class of systems for which chaos and regularity
coexist because the break-up of regular structure as a
function of deformation is gradual. Semiclassical theory for
such ``mixed systems'' is as yet incomplete.
In a microdisk that has been deformed in a smooth and
everywhere convex manner, the WG orbits closest to the edge
remain intact because they skip along the interface in short,
almost grazing line segments, across which the surface
curvature changes only infinitesimally [24]. Chaos first appears in the neighborhood of
certain short periodic orbits which become unstable under
slight variations of their initial conditions. However, other
periodic orbits are stabilized by the perturbation, and the
resulting mixture of chaotic and regular motion is difficult to
disentangle when conventional ray traces are plotted in
real-space.
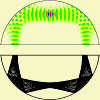
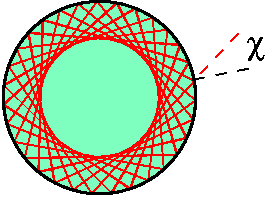
We therefore image the internal ray dynamics in phase
space, using a Poincaré surface of section (SOS)
[25], cf. Fig. 2. The SOS
stroboscopically reveals the combinations of positions
(parametrized by polar angle 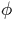 ) and angles of
incidence
) and angles of
incidence 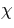 at which different trajectories
impinge on the boundary. Regular orbits typically form
one-dimensional lines that are grouped into islands of
stability, while chaotic rays fill out two-dimensional clouds -
a consequence of the missing constraint of angular-momentum
conservation.
at which different trajectories
impinge on the boundary. Regular orbits typically form
one-dimensional lines that are grouped into islands of
stability, while chaotic rays fill out two-dimensional clouds -
a consequence of the missing constraint of angular-momentum
conservation.
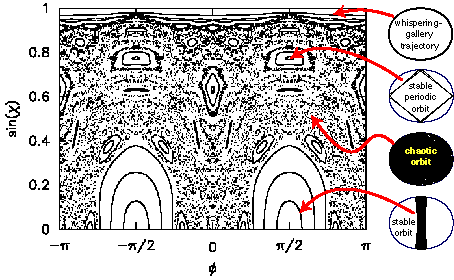
In the WG region corresponding to 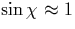 , chaotic motion is characterized by an
approximate separation of time scales: although a chaotic ray
launched in the WG region will eventually explore all
accessible areas of the SOS, it can describe almost
one-dimensional lines for intermediate times because
, chaotic motion is characterized by an
approximate separation of time scales: although a chaotic ray
launched in the WG region will eventually explore all
accessible areas of the SOS, it can describe almost
one-dimensional lines for intermediate times because
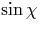 fluctuates only weakly over many
rotations in
fluctuates only weakly over many
rotations in 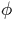 . This slow diffusion in
. This slow diffusion in
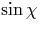 is directed toward lower values,
but the intermediate almost-regular motion can be characterized
by an adiabatic invariant for which we then perform a
semiclassical quantization in the spirit of the eikonal (EBK)
approach [26].
is directed toward lower values,
but the intermediate almost-regular motion can be characterized
by an adiabatic invariant for which we then perform a
semiclassical quantization in the spirit of the eikonal (EBK)
approach [26].
Our eikonal theory not only provides the frequency shifts of
chaotic WG resonances [26], but also
relates each quantized WG mode to a particular adiabatic
invariant curve (AIC) in the SOS. While diffusion in
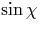 away from that curve can be
neglected in the constructive-interference argument leading to
the mode quantization [21], diffusion is
crucial for determining lifetime and emission directionality.
The reason is that
away from that curve can be
neglected in the constructive-interference argument leading to
the mode quantization [21], diffusion is
crucial for determining lifetime and emission directionality.
The reason is that 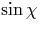 determines the
reflectivity R of the interface: At refractive index
n, Fresnel's formula yields a jump (rounded by
tunneling) from R=1 to a lower value near
determines the
reflectivity R of the interface: At refractive index
n, Fresnel's formula yields a jump (rounded by
tunneling) from R=1 to a lower value near 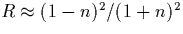 when
when 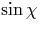 drops below
drops below 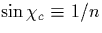 , which
delimits the total-internal-reflection condition.
, which
delimits the total-internal-reflection condition.
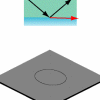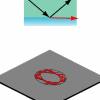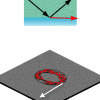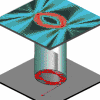
If a threshold deformation [27] is exceeded such that a chaotic domain in
the SOS connects the quantized AIC with the critical value
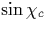 , the average lifetime of rays
launched from this AIC is dominated not by the small
tunnel leakage known from the circle, but instead by classical
phase-space diffusion that allows
, the average lifetime of rays
launched from this AIC is dominated not by the small
tunnel leakage known from the circle, but instead by classical
phase-space diffusion that allows 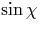 to
reach values where refractive escape (following Snell's law)
can occur. This classically allowed escape mechanism is
wavelength-independent, and one thus expects a
universal resonace lifetime for all chaotic WG modes
supported by the same AIC. Comparison with exact wave solutions
(Fig. 3) confirms this prediction, showing moreover a
quantitative agreement between resonance lifetimes and
classical diffusion times at large deformations -
which is precisely the regime in which wave
calculations are especially difficult!
to
reach values where refractive escape (following Snell's law)
can occur. This classically allowed escape mechanism is
wavelength-independent, and one thus expects a
universal resonace lifetime for all chaotic WG modes
supported by the same AIC. Comparison with exact wave solutions
(Fig. 3) confirms this prediction, showing moreover a
quantitative agreement between resonance lifetimes and
classical diffusion times at large deformations -
which is precisely the regime in which wave
calculations are especially difficult!
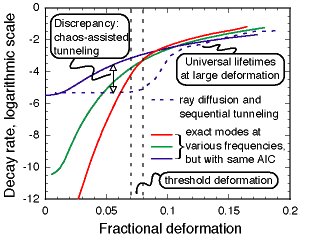
The classical picture proves even more useful when the
emission directionality of a metastable state is
required - a property that is directly observable in
microlasers, whereas it is typically averaged out in nuclear or
chemical decay processes and hence has not been studied in
detail prior to our work. The anisotropic structure of the SOS
in the neighborhood of 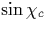 causes
rays to escape preferentially at certain
causes
rays to escape preferentially at certain 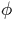 with
with 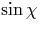 only slightly below
only slightly below
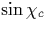 [28]. As
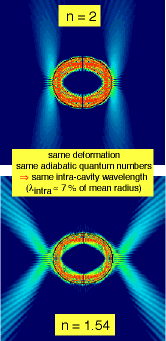
a dramatic consequence, we predict that the emission profile of
an oval cylinder resonator can depend strongly on its
refractive index, even if all other parameters (i.e.
deformation and wavelength) are kept fixed (Fig. 4). This
is because a change in n may place
[28]. As
a dramatic consequence, we predict that the emission profile of
an oval cylinder resonator can depend strongly on its
refractive index, even if all other parameters (i.e.
deformation and wavelength) are kept fixed (Fig. 4). This
is because a change in n may place 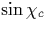 in a part of the SOS where island structure
strongly modifies the chaotic diffusion of WG rays [29]. Applying an analogous phase-space analysis
to nonspherical lasing microdroplets, we explained their
experimentally observed anisotropic emission [30,31].
in a part of the SOS where island structure
strongly modifies the chaotic diffusion of WG rays [29]. Applying an analogous phase-space analysis
to nonspherical lasing microdroplets, we explained their
experimentally observed anisotropic emission [30,31].
Finally, comparing with numerical wave solutions, we can
extract wave corrections to the ray theory, thereby
identifying the physics that is not contained in an essentially
classical model for the metastable states. At deformations too
small to permit chaotic diffusion from the AIC, decay rates are
found to be enhanced over the classical prediction by
chaos-assited tunneling. At large deformations, on the
other hand, chaotic diffusion toward the escape condition can
be suppressed by wave interference, leading to dynamical
localization [26]. These are
phenomena of great current interest in quantum chaos.
Micro-optics and quantum chaos, two fields with rather
different objectives, have thus found a promising connection
from which optical device design can benefit and new
theoretical questions emerge.
| 1 |
Optical Effects associated with small
particles, P. W. Barber and R. K. Chang, eds. (World
Scientific, Singapore, 1988) |
| 2 |
Y. Yamamoto and R. E. Slusher, Physics Today 46,
66 (June 1993) |
| 3 |
J. Rarity, C. Weisbuch, eds., Microcavities and
Photonic Bandgaps: Physics and Applications (Kluwer
Academic Publishers, 1995) |
| 4 |
Optical processes in Microcavities, R. K.
Chang and A. J. Campillo, eds. (World Scientific,
Singapore, 1996) |
| 5 |
J. P. Zhang, D. Y. Chu, S. L. Wu,S. T. Ho, W. G. Bi, C.
W. Tu and R. C. Tiberio, Phys. Rev. Lett. 75, 2678
(1995) |
| 6 |
M. L. Gorodetsky, A. A. Savchenko and V. S. Ilchenko,
Opt. Lett. 21, 453 (1996) |
| 7 |
L. Collot, V. Lefevre-Seguin, M. Raimond and S.
Haroche, Europhys. Lett. 23, 327 (1993). |
| 8 |
B. R. Johnson, J. Opt. Soc. Am. 10, 343
(1993) |
| 9 |
In the circular disk resonator, the out-of plane
component of the wave equation can be approximately
separated from the in-plane propagation for two limiting
cases: if the disk's thickness permits exactly one vertical
mode, or if its refractive index is large enough to render
it effectively closed. In microdisk lasers, the former
condition is usually satisfied. |
| 10 |
A. Dodabalpur, E. A. Chandross, M. Berggren and R. E.
Slusher, Science 277, 1787 (1997) |
| 11 |
M. Kuwata-Gonokami et al., Opt. Lett.
20, 2093 (1995) |
| 12 |
A. Serpengüzel, S. Arnold and G. Griffel, Opt.
Lett. 20, 654 (1995) |
| 13 |
R. K. Chang, J. U. Nöckel and A. D. Stone, U. S.
Patent 5,742,633 (registered April 21, 1998) |
| 14 |
J. U. Nöckel and A. D. Stone, in Optical
processes in Microcavities, R. K. Chang and A. J.
Campillo, eds. (World Scientific, Singapore, 1996) |
| 15 |
H. M. Lai, C. C. Lam, P. T. Leung and K. Young, J. Opt.
Soc. Am. B 8, 1962 (1991) |
| 16 |
Md. M. Mazumder, D. Q. Chowdhury, S. C. Hill and R. K.
Chang, in Optical processes in Microcavities, R.
K. Chang and A. J. Campillo, eds. (World Scientific,
Singapore, 1996) |
| 17 |
M. C. Gutzwiller, Chaos in Classical and Quantum
Mechanics (Springer, New York 1990) |
| 18 |
J. B. Keller and S. I. Rubinow, Ann. Phys. 9, 24
(1960). |
| 19 |
M. V. Berry and K. E. Mount, Rep. Prog. Phys.
35, 315 (1972) |
| 20 |
M. S. Child, Semiclassical Mechanics with Molecular
Applications, 189 (Clarendon Press, Oxford, 1991) |
| 21 |
W. H. Miller, J. Chem. Phys. 48, 1651
(1968) |
| 22 |
R. A. Marcus, J. Chem. Phys. 54, 3965
(1971) |
| 23 |
P. Gaspard and S. A. Rice, J. Chem. Phys. 90,
2242 (1988) |
| 24 |
V. F. Lazutkin, Math. USSR Izvestija 7,
185 (1973) |
| 25 |
The Poincaré surface of section is a central
tool in nonlinear dynamics. In our case, it is obtained
numerically by following a number of rays for several
hundred reflections and recording not only the successive
positions at which the surface is encountered, but also the
angles of incidence 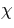 with
respect to the surface normal. The position along the rim
can be parametrized by the polar angle with
respect to the surface normal. The position along the rim
can be parametrized by the polar angle 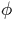 , and each trajectory then generates a set of
points in a graph of , and each trajectory then generates a set of
points in a graph of 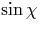 versus versus
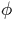 . . |
| 26 |
J. U. Nöckel and A. D. Stone, Nature 385,
45 (1997) |
| 27 |
J. U. Nöckel, A. D. Stone and R. K. Chang, Opt.
Lett. 19, 1693 (1994). |
| 28 |
Often, the escape in fact occurs from the
highest-curvature points as is intuitively expected. This
is another consequence of the slow diffusion in 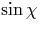 , and it applies to resonators whose
refractive index is sufficiently small to place the
total-internal-reflection condition , and it applies to resonators whose
refractive index is sufficiently small to place the
total-internal-reflection condition 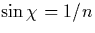 in the WG region of the SOS. However,
stable islands always have to be avoided by chaotically
diffusing rays, and this causes deviations from intuitive
expectations. in the WG region of the SOS. However,
stable islands always have to be avoided by chaotically
diffusing rays, and this causes deviations from intuitive
expectations. |
| 29 |
J. U. Nöckel, A. D. Stone, G. Chen, H. Grossman
and R. K. Chang, Opt. Lett. 21, 1609 (1996) |
| 30 |
A. Mekis, J. U. Nöckel, G. Chen, A. D. Stone and
R. K. Chang, Phys. Rev. Lett. 75, 2682 (1995) |
| 31 |
The microdroplet is one of the pioneering microcavity
systems, but the emission anisotropy of such droplets in
prolate and oblate phases of their natural shape
oscillation had remained unexplained for approximately ten
years prior to our work. |
This page © Copyright Jens
Uwe Nöckel, 01/2002