Editing, copying and pasting Mathematica equations via LaTeX
Here is some information on how to convert formulas from Mathematica to LaTeX and vice versa (see also this post).
For my writing I always use LyX, a LaTeX editor and front end that can format equations while you type them.
Some people prefer to do all their writing in Mathematica. However, for larger documents, I find that impractical. because important editor functions (such citation management, and publication-ready PDF output) are missing. This is the reason why I do the bulk of my writing in LyX – it is not only a LaTeX frontend, but it moreover leaves you immense freedom to customize and export the document.
In going back and forth between Mathematica and LyX, it's convenient that both of them understand LaTeX. Although LaTeX code is semantically ambiguous, it can serve as a bridge connecting these applications.
If you're not interested in using LaTeX, look instead at converting Mathematica formulas to PDF.
Copying individual equations
This is a selective approach that works well when you aren't interested in moving text between Mathematica and LaTeX, only equations:
- Create LaTeX code from arbitrary Mathematica expressions:
The Mathematica function
TeXFormproduces a LaTeX representation of a syntactically correct expression, often trying to apply conventional typesetting rules. The result looks similar but not identical toTraditionalFormoutput.- The general approach is as follows:
TeXForm[HoldForm[ Integrate[f[\[Theta]], {\[Theta], -\[Pi], \[Pi]}]]]
Here, I useHoldForm(alternatively:Unevaluated) to get theLaTeXcode for the input expression,\int_{-\pi }^{\pi } f(\theta ) \, d\theta, not the evaluated result of the integral.Note that this is different from what you get by clicking the cell and selecting
Copy as ... LaTeX: that will give you the literal cell text in the form\text{Integrate}[f[\theta ],\{\theta ,-\pi ,\pi \}], which is a much less usefulLaTeXexpression for presentation purposes.The "less useful" copy-as-LaTeX method is actually quite useful when you're not dealing with valid code expressions, such as this text cell containing a typical math formula in box notation:
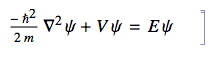
As input to TexForm, this would be nonsense because there's no intepretation for the∇2symbol, and the equal sign acts as an assigmnent. ButCopy as ... LaTeXworks perfectly in this situation.The
TeXFormapproach is the one you would usually choose in order to transfer the output of a Mathematica evaluation to LaTeX. On the other hand, the menu approach allows you to get the LaTeX form of inline or displayed equations in a Mathematica Notebook. - Tweaking the output in special situations:
Because notational tastes vary, it is likely that not every valid expression will be translated into the TeX form you expect.
For derivatives, there are several different display formats, and you can influence which one Mathematica chooses by specifying the format of the output. The situation is discussed in this post on the Wolfram Blog. On that page, I am also giving an example expression that contains several different types of derivatives:
d = D[f[g[x]] + h[x, y], {x, 2}]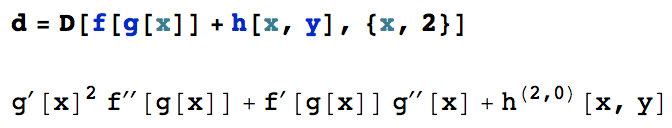
The derivative notation that you get from both
TeXForm[d]andTraditionalForm[d]doesn't make use of the standard (fraction-like) notation for derivatives. Motivated by the comments on the blog post linked above, my suggestion is to modify theTraditionalFormhandling of derivatives as follows:Derivative /: MakeBoxes[Derivative[\[Alpha]__][f1_][vars__Symbol], TraditionalForm] := Module[{bb, dd, sp}, MakeBoxes[dd, _] ^= If[Length[{\[Alpha]}] == 1, "\[DifferentialD]", "\[PartialD]"]; MakeBoxes[sp, _] ^= "\[ThinSpace]"; bb /: MakeBoxes[bb[x__], _] := RowBox[Map[ToBoxes[#] &, {x}]]; FractionBox[ToBoxes[bb[dd^Plus[\[Alpha]], f1]], ToBoxes[Apply[bb, Riffle[Map[bb[dd, #] &, Select[({vars}^{\[Alpha]}), (# =!= 1 &)]], sp]]]] ]
I copied the code from my post so that you can copy it into a Notebook directly from here without having to correct the quotation marks that came out wrong on the blog (Wolfram should really get to work on a proper
HTML-ization utility for their blog posts and online help — it doesn't reflect well on MMA if their web pages rely on bitmap images to display notebook content). With this, the output ofTeXForm[d]andTraditionalForm[d]looks much nicer (I'm only showing theTraditionalFormoutput – theLaTeXoutput is very similar):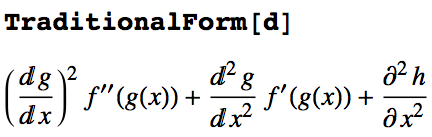
Now you have partial derivative symbols where two or more variables are involved, total derivative symbols where only one variable appears, and primes where the differentiation is with respect to a function slot that isn't one of the differentiation variables.
In the above definition, the second argument
f1to theDerivativefunction is always the name of a function. If you expect to encounter the non-standard case wheref1is something more complex (like a sum of symbols), it would be better to not use my abbreviated notation. You can rule such cases out by replacing[f1_]with[f1_AtomQ]in theDerivativepattern.
- The general approach is as follows:
- Create Mathematica expressions from copied LaTeX code:
The first thing to realize is that LaTeX is great for presenting conventional math notation, but it often leaves room for interpretation, so that the structure of an expression cannot always be guessed correctly by Mathematica. For example, a derivative is often written in a way that looks like a fraction, and one needs some comventions to decide which is which.
- The general approach is as follows:
ToExpression["\\int_{-\\pi }^{\\pi } f(\\theta) \\, d\\theta", TeXForm, Hold]
Note that all backslashes are doubled because a single\counts as an escape character. In the above code, the argumentHoldprevents evaluation so you can copy the expression from the output cell if desired (you can later applyReleaseHoldto evaluate the expression). This conversion will throw an error if Mathematica thinks the expression has incorrect syntax. So you won't always be able to get literal translations of arbitraryLaTeXfragments. - Some specific hints for common expressions:
- Spaces are completely ignored by Mathematica, even in products of variables such as
z = x y. The Mathematica expression will become z = xy which incorrectly references a single variable with a two-letter namexy. You have to explicitly insert thin spaces ("\\,") in the string argument ofToExpressionwherever you want an implicit multiplication to appear. Note thatLaTeXignores spaces too, but it defaults to defining each letter as a separate variable in the above expression. Mathematica simply uses the wrong default assumption here. - Spaces between digits as in
3.1 103are also ignored, so this example would be translated as(3.11)3. As above, you have to force Mathematica to recognize spaces, or use a multiplication operator such as\timesin yourLaTeXcode. - To translate integrals properly, Mathematica expects the integration
variable in the
LaTeXcode to be preceded by\\, d. Only with the additional space will it recognize thedas the differential part of the integral. - Express derivatives using the
\partialsymbol:
ToExpression["\\frac{\\partial^2 f(x)}{\\partial x^2}", TeXForm, Hold] - All matrices and vectors must be written in list form using
escaped curly brackets, as in
\{x,y,f (z)\}
because the conversion ofarrayenvironments or commands such as\pmatrixto Mathematica produces wrong formatting. -
To group expressions, use only round parentheses, i.e.,
\left(and\right), not square[...]or curly{...}brackets. The latter are interpreted differently by Mathematica.
- Spaces are completely ignored by Mathematica, even in products of variables such as
- The general approach is as follows:
- When Mathematica fails to translate from
LaTeX, create a snippet of the MMA code that you think should be generated. Put this intoTeXForm. From the result, you can often guess the requiredLaTeXform that will work in reverse as an input toToExpression.
Exporting an entire Mathematica Notebook as LaTeX
This approach is sometimes necessary, but I would suggest trying the previous approach first, because the exported equations are almost certainly not going to be coded as real LaTeX equation environments.
To bring a whole Mathematica Notebook into LaTeX format, you can do this via the File > Export menu. However, there are some restrictions that one should keep in mind to avoid surprises:
- Use a simple style sheet.
- Use only the basic cell styles: from Title to Subsubsection, also Input, Text, DisplayFormula, DisplayFormulaNumbered.
- Before exporting, convert all cells that contain graphics (including ListAnimate etc.) to bitmap (from the Cell menu). Otherwise the generated EPS files are huge and sometimes fail to convert for preview in LyX
- Don't use long passages of bold face in your text cells.
All exported boldface is wrapped in
\pmb{ }(that's poor man's bold, and it deserves the name) - Avoid comments in Mathematica code of the type
(* ... *)because inter-word spaces are omitted upon export. - There are several other bugs that can produce uncompilable
LaTeXoutput.
Finally, even if you decide to export the whole document to LaTeX, it will generally be necessary to go through the source with a text editor to clean up formatting problems.
Last modified: Thu Mar 31 10:23:15 PDT 2022