This is the HTML version of a Mathematica 8/9 notebook. You can copy and paste the following into a notebook as literal plain text. For the motivation and further discussion of this notebook, see "Mathematica density and contour Plots with rasterized image representation"
The function gradientFieldPlot takes a scalar potential with two independent variables as its first argument: φ(x, y). The second and third arguments are the name and range of the independent variables, e.g., {x, xmin, xmax} and {y, ymin, ymax}.
The plot contains three elements:
φ, ∇φ,∇φ (they are everywhere perpendicular to the contour lines of the potential).gradientFieldPlot[f_, rx_, ry_, opts : OptionsPattern[]] := Module[ { img, cont, densityOptions, contourOptions, frameOptions, gradField, field, fieldL, plotRangeRule, rangeCoords }, densityOptions = Join[ FilterRules[{opts}, FilterRules[Options[DensityPlot], Except[{Prolog, Epilog, FrameTicks, PlotLabel, ImagePadding, GridLines, Mesh, AspectRatio, PlotRangePadding, Frame, Axes}]]], {PlotRangePadding -> None, Frame -> None, Axes -> None, AspectRatio -> Automatic} ]; contourOptions = Join[ FilterRules[{opts}, FilterRules[Options[ContourPlot], Except[{Prolog, Epilog, FrameTicks, PlotLabel, Background, ContourShading, PlotRangePadding, Frame, Axes, ExclusionsStyle}]]], {PlotRangePadding -> None, Frame -> None, Axes -> None, ContourShading -> False} ]; gradField = ComplexExpand[{D[f, rx[[1]]], D[f, ry[[1]]]}]; fieldL = DensityPlot[Norm[gradField], rx, ry, Evaluate@Apply[Sequence, densityOptions]]; field=First@Cases[{fieldL},Graphics[__],\[Infinity]]; img = Rasterize[field, "Image"]; plotRangeRule = FilterRules[Quiet@AbsoluteOptions[field], PlotRange]; cont = If[ MemberQ[{0, None}, (Contours /. FilterRules[{opts}, Contours])], {}, ContourPlot[f, rx, ry, Evaluate@Apply[Sequence, contourOptions]] ]; frameOptions = Join[ FilterRules[{opts}, FilterRules[Options[Graphics], Except[{PlotRangeClipping, PlotRange}]]], {plotRangeRule, Frame -> True, PlotRangeClipping -> True} ]; rangeCoords = Transpose[PlotRange /. plotRangeRule]; If[Head[fieldL]===Legended,Legended[#,fieldL[[2]]],#]&@ Apply[Show[ Graphics[ { Inset[ Show[SetAlphaChannel[img, "ShadingOpacity" /. {opts} /. {"ShadingOpacity" -> 1}], AspectRatio -> Full], rangeCoords[[1]], {0, 0}, rangeCoords[[2]] - rangeCoords[[1]]] }], cont, StreamPlot[gradField, rx, ry, Evaluate@FilterRules[{opts}, StreamStyle], Evaluate@FilterRules[{opts}, StreamColorFunction], Evaluate@FilterRules[{opts}, StreamColorFunctionScaling], Evaluate@FilterRules[{opts}, StreamPoints], Evaluate@FilterRules[{opts}, StreamScale]], ## ] &, frameOptions] ]
Here is an example of how to use the function. The contour lines of the potential are shown in white, and the streamlines of the gradient field are orange.
gradientFieldPlot[ (y^2 + (x - 2)^2)^(-1/2) - (y^2 + (x - 1/2)^2)^(-1/2)/2, {x, -1.5, 2.5}, {y, -1.5, 1.5}, PlotPoints -> 50, ColorFunction -> "BlueGreenYellow", Contours -> 10, ContourStyle -> White, Frame -> True, FrameLabel -> {"x", "y"}, ClippingStyle -> Automatic, Axes -> True, StreamStyle -> Orange]

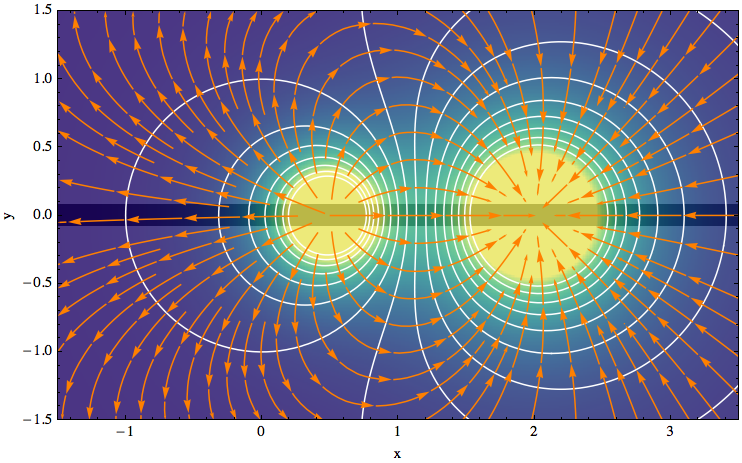
But perhaps you would like to emphasize the horizontal axis by making it really thick. Now you can achieve this without obscuring the plot:
gradientFieldPlot[(y^2 + (x - 2)^2)^(-1/ 2) - (y^2 + (x - 1/2)^2)^(-1/2)/2, {x, -1.5, 3.5}, {y, -1.5, 1.5}, PlotPoints -> 50, ColorFunction -> "BlueGreenYellow", Contours -> 16, ContourStyle -> White, Frame -> True, FrameLabel -> {"x", "y"}, ClippingStyle -> Automatic, StreamStyle -> Orange, ImageSize -> 500, GridLinesStyle -> Directive[Thick, Black], "ShadingOpacity" -> .8, Axes -> {True, False}, AxesStyle -> Directive[Thickness[.03], Black], Method -> {"AxesInFront" -> False}]