
This happens for example in zeolite microcrystals that are doped with an organic dye as "guest" molecules. The dye is able to emit light by fluorescence, and because of the imposed orientation of the organic molecules in their host matrix, the light is polarized.

The nanopores of the zeolite form a "molecular sieve" with a
hexagonal arrangement. If one grows crystallites out of this
material, this translates into a hexagonal facet
structure. The light generated by the fluorescent dye molecules
now gets trapped inside this self-assembled hexagonal
microresonator by reflecting off the facets. The polarization
properties of the medium favor propagation in a cross-sectional
plane of the crystal, whose size is below 10 micron
diameter.
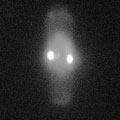
These tiny grains of hybrid material can in fact be made into extremely small lasers. Apparently, the light is trapped sufficiently long to provide the necessary feedback for light amplification. But pores in a material usually reduce the overall refractive index n, and in fact the zeolite-dye system has n=1.45 - this makes it easy for rays in such a resonator to escape to the surrounding air by the law of refraction.
![]()
All orbits here have the same angle of incidence, and the
same length. They constitute a family of rays, all of which
can be expected to make a contribution to the resonator modes.
There is nothing a priori that singles out the symmetric
inscribed hexagon (left), and in fact admixtures from all of
these orbits can contribute to any single mode.
What about their escape behavior? Total internal reflection
confines these modes, but the classical Fresnel formulas
break down at the corners. The degenerate periodic orbit
hitting the corners (right) is therefore special because simple
total internal reflection doesn't work there. So the
corners are where the escape should happen in a
preferred way.
That is in fact what is seen in experiment and also what I find in my wave simulations. Here is an example:
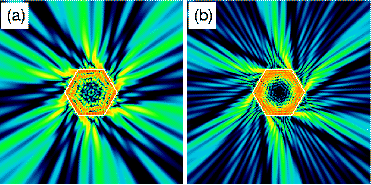
This is for microcryastals with n=1.45 at (a) 4 and (b) 8
micron diameter, wavelength 600…700 nm. To read more
about the "pinwheel-like" asymmetry in the
emission, follow this link.
The experiments were carried out by Uwe Vietze and Franco Laeri. This group in Darmstadt, in collaboration with Bremen University and the MPI für Kohleforschung did the pioneering development leading to zeolite nanocomposites with lasing action. For the small cavities studied here, the ray picture doesn't give a correct description of the actual emission pattern due to strong corner diffraction.
Together, we conducted a comprehensive investigation of this micro-optical system, published in Applied Physics B, see also my publication list.
The hexagonal resonator is interesting from a theoretical point of view because its internal dynamics is pseudointegrable, a pathological condition. It causes the rays patterns to look rather neat compared with a chaotic cavity - but don't let this fool you. Even if we neglect the copmplication of leakage from the resonator, the wave fields for this system cannot be written down in any simple way, except for a subset of solutions whose intensity vanishes on all the diagonals (and hence in particular on the corners). But the interesting solutions are precisely those with nonzero intensity on the diagonals, because the ray picture tells us that those types of fields favor escape at the corners.
The pathological properties of pseudointegrable systems can be studied especially well in polygonal billiards , and in this way the importance of diffraction as a correction to geometric optics is revealed.
The theoretical interest in the hexagonal resonator combines
in an ideal way with the great significance of this geometry in
naturally occuring and artificially engineered micro-optical
systems. Perhaps the first hexagonal microstructure that comes
to mind is in fact the snow crystal
(that's what snowflakes are made of) . In tropical cirrus
clouds, such crystals are less than 50 micron small, i.e. they
are micro-optical systems. Their scattering properties are of
great importance in meteorology because of their potential
climatic effects. Of course, people have not been that
interested in the possibility of long-lived resonances in
snowflakes... certainly my kids are more interested in the
lifetime of the snowflake itself.
Photonic states in a hexagon are, however, very important when
it comes to microlasers made of Gallium Nitride - one of the
most promising candidates for the elusive goal of producing
blue light with a semiconductor laser diode. This compound
grows with a hexagonal facet structure as well !
This page © Copyright Jens Uwe Nöckel, 06/2003
Last modified: Mon Mar 14 20:05:51 PDT 2011