Diminutive Domes

Exact wave solutions for confocal paraboloids

The detailed discussion which includes more considerations concerning polarization can be found in the paper. Only the basic ideas are given here. In cylinder coordinates, we can assume the azimuthal dependence

of the wave field, and thus reduce the Helmholtz equation

to the separated form

This can be further separated in parabolic cylinder coordinates by making the ansatz

The terms in brackets represent an effective potential in analogy to the Schrödinger equation of quantum mechanics, which is plotted above.
The separation constant is K, and the resulting ordinary (one-dimensional) differential equations are coupled with each other.

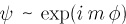
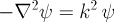
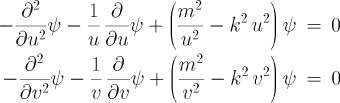
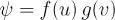
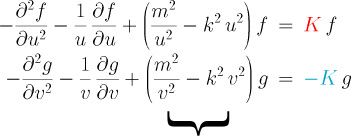
The effective potential is the same for both differential equations (for f and g). But the "energy eigenvalue" of these two Schrödinger-like equations are K and -K, respectively, so that one is above and one is below zero (or both can be zero, of course).
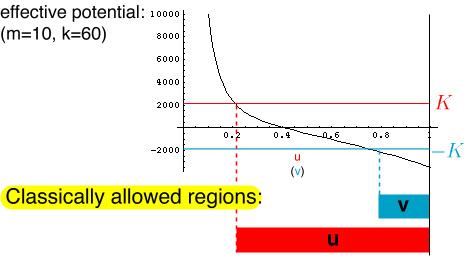
This is illustrated in the above potential picture with the thin red and blue horizontal lines at +K and -K. The horizontal axis in the plot is the coordinate u or v. The boundaries of the double paraboloid are located at u = 1 and v = 1.

As usual for this type of differential equation, one expects high amplitude only in the classically allowed regions of the potential, i.e., where the horizontal line is higher than the potential. The resulting classically allowed ranges of the coordinates u and v are shown at the bottom as red and blue bars.

The central point about the wave equations for f and g is the coupling of the two by way of the constants k and K. We can make the equations look slightly simpler by putting

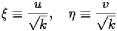
which leads to the equations

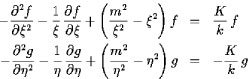
However, the boundary conditions are now imposed at ξ, η = Sqrt(k).

Now we have to specify the boundary conditions. For simplicity, I will consider the typical Dirichlet boundary conditions, i.e. f and g should vanish on the paraboloid surfaces.

How to impose the boundary conditions for these coupled equations ?

The real-valued wave solutions are proportional to Kummer's confluent hypergeometric function M,

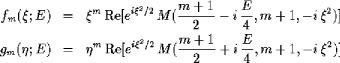
The separation constant K (or beta) here enters as E=K/k.
The boundary condition of vanishing wavefunction at

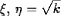
means that the separate roots of the equations

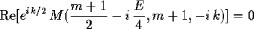
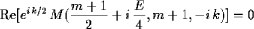
have to exist simultaneously.

To find these points in the k-E plane, we plot the roots of these separate equations on top of each other and look for the crossings of the curves defined by the equations.

This is done here for the lowest angular momenta m=0...5 (from top left to bottom right):

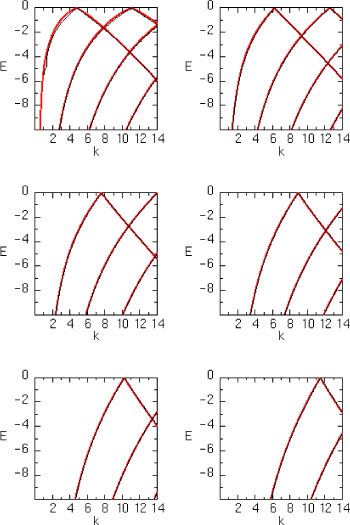
The black lines are the curves obtained from the zeros of the equations involving the Kummer functions, the red lines are the same zeros of the corresponding semiclassical condition.
Note the good agreement between the exact and semiclassical zeros.

Click on the plot to see a more exhaustive list of modes.
	k=12.14192329557385, E=-3.100689099111115

The eigenfunction should take into account the reflection symmetry with respect to the plane xi=eta, and this is achieved by forming symmetric and antisymmetric linear combinations of the solutions shown here, with their counterparts in which ξ and η are interchanged. This is not done in this plot because I want exhibit more clearly the resemblance to the classical ray trajectories. This ray-wave correspondence can be seen by comparing the above wave plot to the ray trace in Fig.5 on the ray physics page.

The correpsondence becomes better when k becomes larger. In the comparison, keep in mind that my ray plots are rotated by 90 degrees and cut in half.

Here are the symmetrized wavefunctions with even parity, formed from the above results by using f(ξ)*g(η)+f(η)*g(ξ).

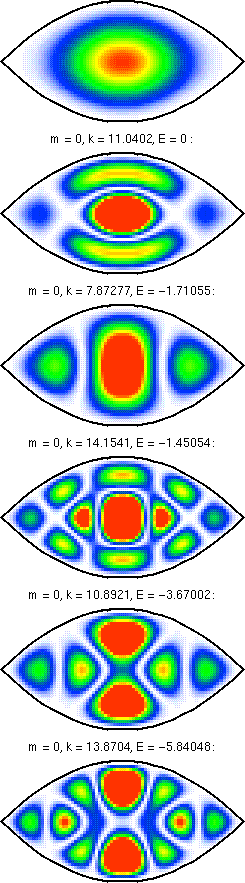
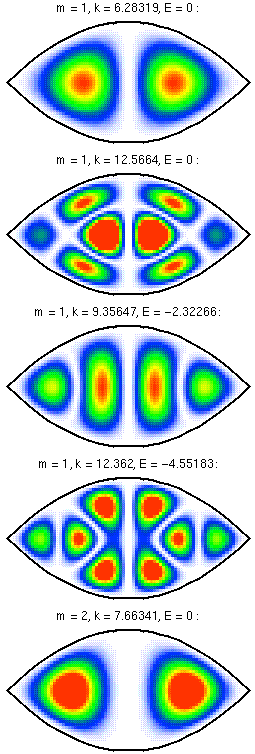
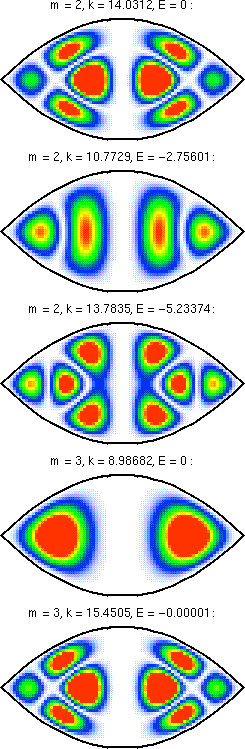
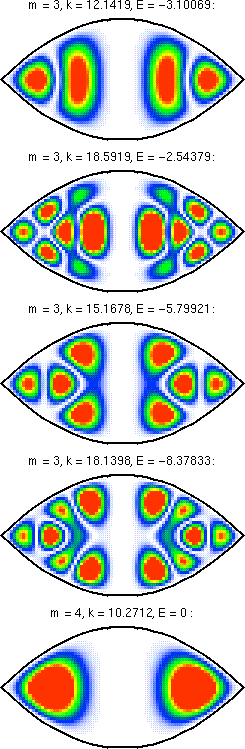
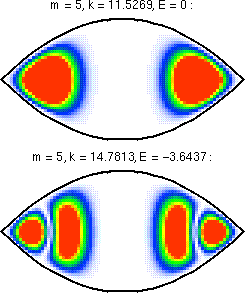
These functions satisfy Neumann boundary conditions on the plane ξ=η, i.e., the plane interscting the focus. This is the actual boundary in the real dome structure, and the Neumann boundary conditions simulate the effect of the Bragg grating.

Last modified: Wed Jan 20 21:05:07 PST 2016