Problems for 8 April 1996

You can hand in the following problems at beginning of class on Monday 8 April. If you have more than one page, please staple them together. And don't forget to include your name. Also, please write at the top near your name that these are the problems for 8 April.

What are comets?
- Reading: Chapter 17 Interplanetary Vagabonds , Section 17-7.
- Questions: 10.
Where are we in the universe?
- Reading: Chapter 26 Galaxies , Introduction and Section 26-1.
- Questions: 1 and 2.
What is the universe made of?
- Reading: Chapter 5 The Nature of Light and Matter , Section 5-6.
- Questions: 14.
What is light, and how is it made?
- Reading: Chapter 5 The Nature of Light and Matter , Sections 5-1, 2,3,4,5,7.
- Questions: 1,4,5,6,7,13,16.
How does the Doppler effect tell us about motion of objects that emit light?
- Reading: Chapter 5 The Nature of Light and Matter , Sections 5-8.
- Questions: 17.

Grader: Di Fidio

Answers to three of the questions

5-1) Appproximately how many times around the world could a beam of light travel in one second.
- The speed of light is c = 3 x 10⁸m/s.
- Thus in one second a light signal can go a distance d = 3 x 10⁸m.
- The circumference of the earth is about a = 4 x 10⁷m.
  - The circumference of the Earth is Pi (3.14) times the diameter of the Earth, given in the Appendix 2 of our book.
  - diameter = 12,756 km.
  - circumference = 3.14 x 12765 km = 40,074 km.
  - 40,000 km = 4 x 10⁴ km = 4 x 10⁴ x 10³ m = 4 x 10⁷ m.
- Thus the light signal can go n = d/a times around the Earth in one second:
  n = 3 x 10⁸m/ 4 x 10⁷m = 0.75 x 10¹ = 7.5
5-5) A light source emits infrared radiation at a wavelength of 825 nm. What is the frequency of this radiation?
- 1 nanometer (nm) is 10^-9 meter.
- Thus the wavelength is 825 x 10^-9 m.
- The frequency is the number of waves that go by per second. It equals the speed of light divided by the wavelength of the light:
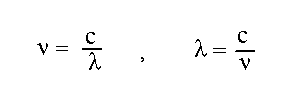
- We calculate
  - frequency = c/wavelength
  - = (3 x 10⁸m/s)/(825 x 10^-9m)
  - = (3 x 10⁸m/s)/(0.825 x 10^-6m)
  - = 3.6 x 10¹⁴ Hz
5-6) Announcers at a certain radio station say that they are at ``103.3 FM on your dial,'' meaning that they tansmit at a frequency of 103.3 MHz. What is the wavelength of the ratio waves from this station?
- 1 MHz is 10⁶ Hz.
- Thus the frequency is 103.3 x 10⁶ Hz.
- The wavelength equals the speed of light divided by the frequency of the wave:
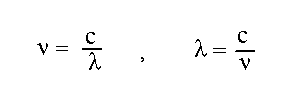
- We calculate
  - wavelength = c/frequency
  - = (3 x 10⁸m/s)/(103.3 x 10⁶Hz)
  - = (3 x 10⁸m/s)/(1.033 x 10⁸(1/s))
  - = 3 m

Davison E. Soper, Institute of Theoretical Science, University of Oregon, Eugene OR 97403 USA soper@bovine.uoregon.edu