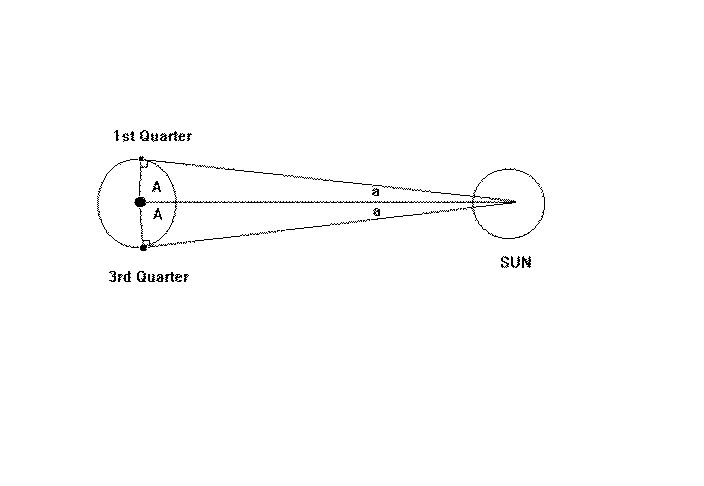
The first step was to show that the Sun was much farther from the Earth than was the Moon.

Aristarchus timed how long it took the Moon to go from 3rd to 1st quarter (t) and then from 1st to 3rd quarter (T). If t = T, then the angle A would be 90 degrees. If t less than T, then the angle would be less than 90 degrees. Note that if A ~ 90 degrees this means that the Sun is much much much much further from the Earth than is the Moon. The smaller the angle A is, the smaller the difference between the distances of the Sun and Moon from the Earth.
Aristarchus performed this exercise (it was difficult because
the angle is very
nearly 90 degrees). His answer was inaccurate, but he found that
that the Sun was 18-20 times further from the Earth than was the Moon
(the current value is 390).
The next step was to infer the relative size of the Sun and the Earth. To accomplish this, Aristarchus used eclipses.

Based on the eclipse geometry shown above, Aristarchus concluded that the Sun must be much larger than the Moon because the angular sizes of the two objects are nearly the same while the Sun is much farther away.
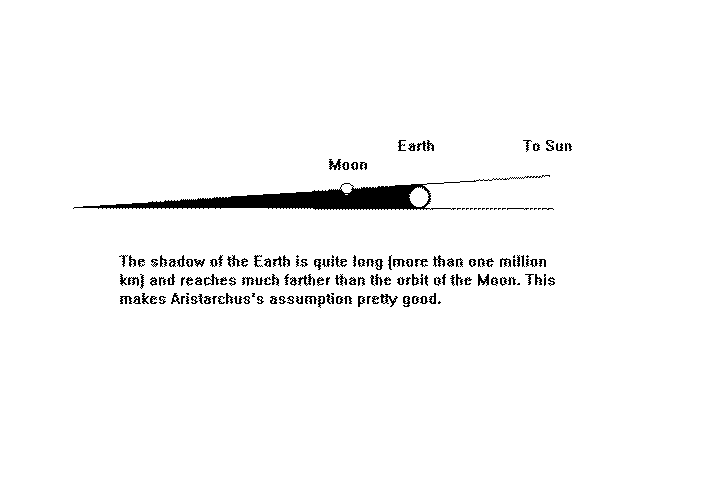
Next, Aristarchus wanted to figure out how large the Moon was compared to the Earth. He decided that the length of the Earth's shadow was much greater than the distance to the Moon and so he could assume that the diameter of the shadow (where the Moon entered it) was roughly the same size as the Earth. Given this, Aristarchus could then simply time how long it took the Moon to pass through the shadow of the Earth and then deduce how large the Moon was compared to the Earth. To see this,
Aristarchus concluded that the Sun was much larger than the Earth and so it was more likely that it lived at the center of our Solar System!