Pieter Bruegel the Elder (1525-1569)

Why Do We Study Stars?

Stars are interesting
Stars are very luminous, L_Sun = 4x10²³ kWatts

indirect energy source
direct energy source

Solar-Terrestrial climate connections
Stars are High-Energy Physics Laboratories
Stellar-Terrestrial connections
Stars are useful probes for the study of the Universe
....

A. THE SUN (and stars) ARE PRODIGIOUS SOURCES OF ENERGY

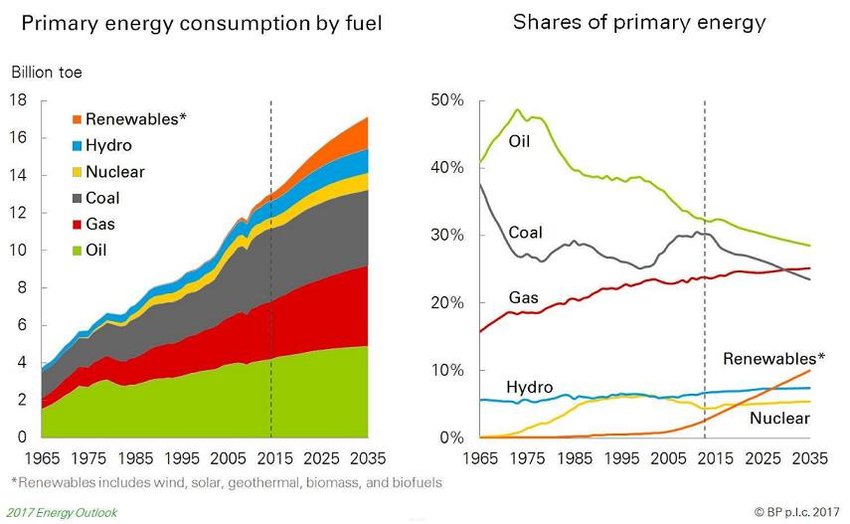World-Wide Energy Consumption

We consume around 15 billon toe (TOE, Tonnes of Oil Equivalent) energy each year. A TOE converted to a more familiar energy unit such as a Joule, is 1 TOE = 4.19x10¹⁰ J.
The total energy consumption, 15 TOE, is then 6.29x10²⁰ Joule !!!!

Another measure of a Joule is that an average person uses around 10 million Joules per day or a person burn s energy at a rate of 10 million Joules per 86,400 s ~ 120 W. That is, a 120 W light bulb supplies roughly the amount of energy needed to power a human. This doesn't sound like too much.
Okay. Let us consider, in practical terms, What is a Joule?

WHAT IS A JOULE? HOW MUCH IS A JOULE?
What is a Joule? A Joule is a unit of energy, where energy is defined as "the ability to do work." What this means is an ability to cause something to move.
How much is a Joule? In people terms, if I say that something carries 1 Joule of energy, what am I to understand this says? Consider mosquitos. The average mosquito has mass 2.5 milligrams (in terms of weight on the Earth, this is ~ 6 millionths of a pound) and mosquitos fly at speeds of 1 or 2 km per hour. A flying mosquito then has kinetic energy ~ 10^-6 Joule, or less than one-millionth of a Joule. A swarm of a million mosquitos considered as a pack, carries total kinetic energy of ~1 Joule! Is this impressive?

As another example, consider the shoe ladder to the right. Imagine that the top rung of the ladder is 2 meters above the ground and that the birkies on the top rung weigh 2 lb (around 1 kilogram). If the pair of birkies fall off the ladder, each would accelerate downward under the pull of gravity. Each shoe strikes hit the ground after about 0.6 seconds, when it is traveling around 6 meters per second or about 14 miles per hour. At the ground, the pair of shoes has kinetic energy of around 20 Joule. If I stepped off a 2 m ladder, I would hit the ground with around 1300 Joule.

The Sun produces 4x10²⁶ Joule every second which, more familiarly, is written 4x10²³ kWatt (kW). Recall that the Earth consumes around 6.29x10²⁰ Joule per year so that the Sun produces enough energy to power the Earth for 1 year every millionth of a second. The Sun is indeed a prodigious source of energy.

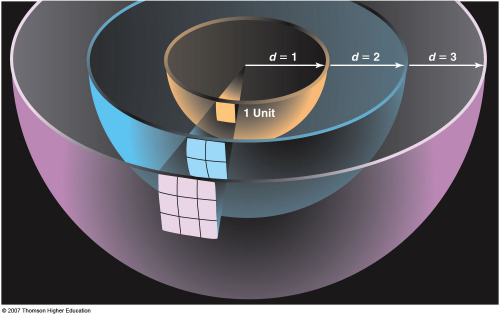INVERSE SQUARE LAW

There is more to the story, however. Because of the large distance of the Sun from the Earth (150,000,000 km), we intercept only a small fraction of the power emitted by the Sun, only about ~2.2x10^-5 of the power per unit area (a quantity known as its energy Flux) emitted by the Sun. The brightness of the Sun (its flux) falls off as 1/D², where D is the distance to the Sun. Although the amount of energy we intercept because of this effect (the inverse square fall-off of the brightness of the Sun) is tiny, the fraction of the Solar power we absorb is large in the sense that the Earth easily intercepts enough energy from the Sun to satisfy our energy needs. The energy that strikes the top of the Earth's atmosphere is 1,361 kWatt per square meter (known as the Solar constant). Allowing for reflection by clouds in our atmosphere (Albedo effects) and absorption of light by our atmosphere (our atmosphere is not completely transparent), the Solar energy which ultimately reaches the ground is still substantial, ~0.34 kWatts per square meter, A Solar collector only ~100 miles x 100 miles in size is capable of capturing enough Solar energy to satisfy the current energy needs of the Earth.

B. SOLAR-TERRESTRIAL CONNNECTIONS (Section 14.3)

Sunspot Cycle and Solar Activity

The Sun exhibits cool blemishes on its surface known as Sunspots. The average temperature of the surface of the Sun is ~5,800 Kelvin. (See the next panel for a description of the different temperature scales we use in this class.) Sunspots are ~4,500 Kelvin. Their lower temperatures makes Sunspots appear darker than the surrounding regions of the Sun (see comments after Stefan-Boltzmann Law [Lecture 3]. Sunspots were discovered by Galileo in the 1600s. In and of themselves, Sunspots are not that significant, but what they are is they are symptomatic of the activity level of the Sun.
The number of Sunspots observed on the Sun varies roughly periodically over time, periods ranging from 7 to 15 y. This was the first observed indication of the Solar Activity Cycle.

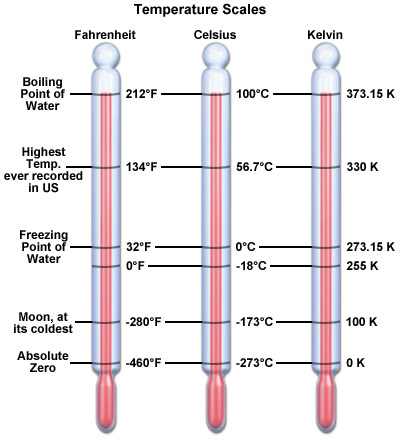Temperature Scales
The most familiar temperature scales are Farenheit and Celsius. The Kelvin scale is related to the Celsius scale and commonly used in the sciences. The Kelvin scale starts at what is referred to as Absolute Zero (-273.15 Celsius [C]); Celsius starts at the freezing point of water.

Kelvin: T(K) = T(C) + 273.15
Celsius: T(C) = (5/9)[T(F)-32 F] -- F stands for Farenheit
At very high temperatures, there is little difference between Kelvin and Celsius temperatures. For example, the average surface temperature of the Sun is 5,800 K which is 5,527 C. The two temperatures are nearly the same. Farenheit, on the other hand, is much different. The Sun at 5,800 K is around 10,000 F!
T(K) = 5,800 Kelvin = 1.8 x 5,800 = 10,440 above absolute zero ===> 10,440 - 460 ~ 9,800 F.

Sunspot Number and Wolf Number

The Sun goes through an activity cycle, The Solar Activity Cycle* with the most obvious manifestation of the varying number of Sunspots on its surface. The Sunspot Number is quantified by the Wolf Number,
Wolf Number = k [ 10 x (Number of Sunspot groups) + (Number of Sunspots)]
The constant k, is a factor included to account for different observers counting different numbers of sunspots. If k is 1, what is the Wolf Number if an observer sees 1 Sunspot?
The Wolf Number varies with a period of 7-15 years with an average length of 11 years. There are other effects which we shall describe later, such as increases in coronal activity, increases in flaring activity, increases in the Solar Wind, and increases in magnetic activity. The cycle is fairly regular having been traced back hundreds of years using tree ring studies and nearly 2,000 years using coral reefs. Although regular, the Sunspot cycle determined using these proxies has shown disruptions. For example in 1645-1715, the cycle may have halted during what is known as the Maunder Minimum

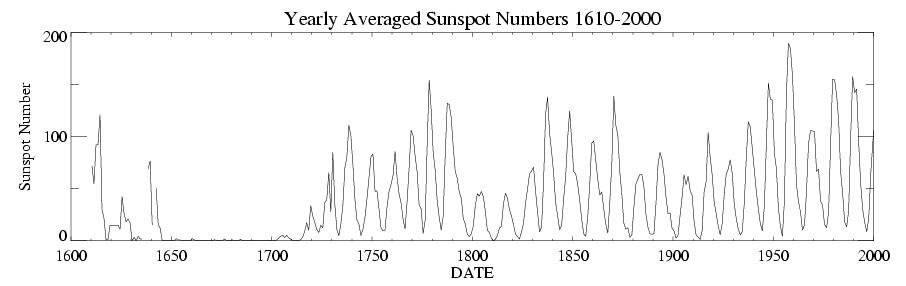Interestingly, at this time, Northern Europe and North America were in the middle of what is referred to as the Little Ice Age (see Discovery 16-2, p. 434 ).

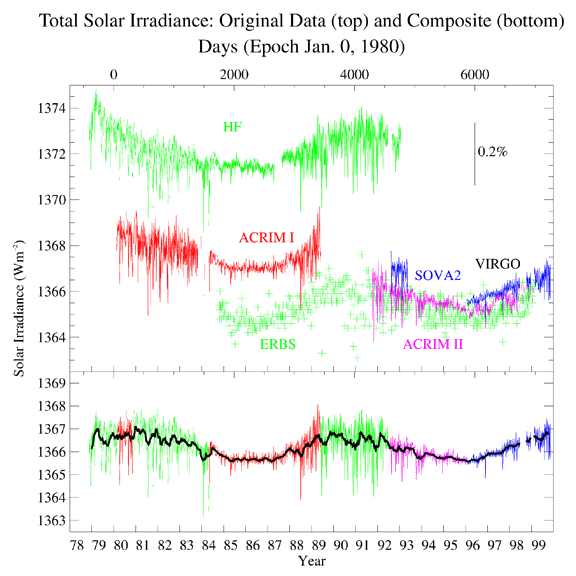Solar Constant

The vexing thing is that although there are measurable changes in the Solar output during the Solar Activity Cycle, the change in the Solar luminosity (as measured by the Solar Constant, see the figure to the left) is small. The Solar Constant varies over the course of the Solar Activity Cycle from 1,367 to 1,365 Watts per square meter, as measured at the top of the Earth's atmosphere. The Sun (somewhat paradoxically) is the brightest at the peak of the Solar Activity Cycle, when the greatest number of sunspots are seen.

Why is how the Solar Constant changes over the Solar Activity Cycle, "somewhat paradoxical?"

The luminosity of the Sun has increased as it has aged; 3.8 billion years ago the Sun was ~25 % fainter than today. This is a conundrum because there was liquid water on the Earth at least 3.7 billion years ago and a simple argument leads to a prediction for what is referred to as the Equilibrium Temperature, T_e for the Earth which at that time, would be below the freezing point of water, T_e = -40 C! Note that T_e is determined by simply finding the temperature for the Earth where it radiates exactly the same amount of energy per second as it receives from the Sun in the absence of clouds and an atmosphere. Further, if we were to include an atmosphere with the composition of our current atmosphere, the temperature would rise but would still be less than the freezing point of water. This is
THE FAINT YOUNG SUN PARADOX

The answer to the question of then, why do we have liquid oceans? requires that our atmosphere in the past had a much different chemical composition than today so that the Greenhouse Effect could maintain liquid oceans because based on the theory of the Sun, we know that the Sun was much brighter in the past than today.

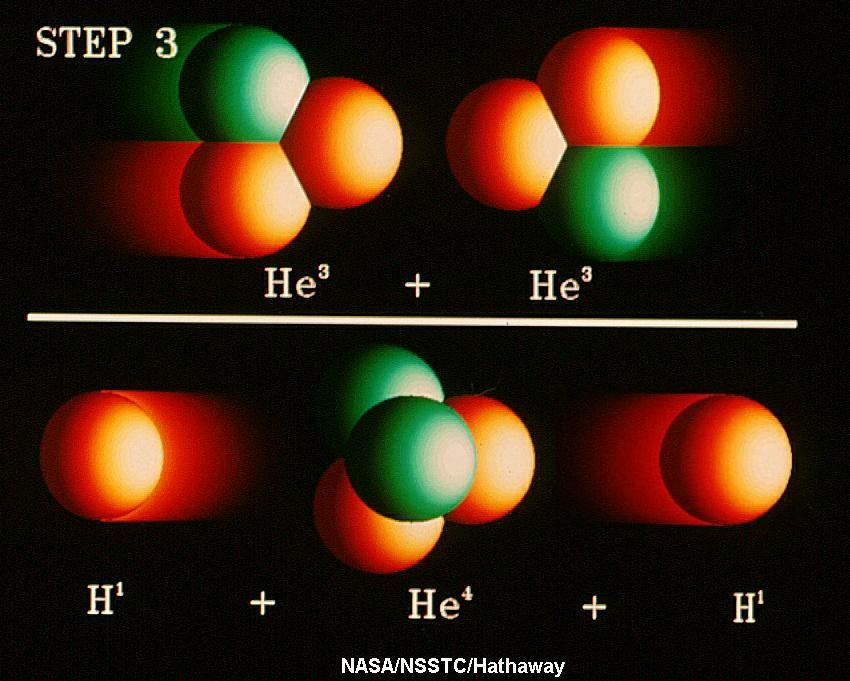
C. STARS AS PHYSICS LABORATORIES: SOLAR NEUTRINOS (Section 14.2)

Normal stars like the Sun produce most of the energy through which they shine through nuclear fusion reactions wherein they build massive elements by combining together (fusing) less massive elements converting some of the mass to energy. In the Sun, the energy is produced through what is called the Proton-Proton Chain, the fusion of four hydrogen nuclei into a helium nucleus plus some other fundamental particles and energy (see Section 14-2). The energy for us is the most important part of the process, but it turns out the byproducts of the proton-proton chain reactions, the ghostlike particles known as neutrinos (ν) have played a large role in our understanding of the physics of the Sun.
If we truly understand how the Sun (and stars) produce energy and shine, a predictable amount of accompanying νs will also be produced. Now, something that makes neutrinos extra interesting is that because of how large and massive is the Sun, the energy produced in its interior through nuclear reactions, takes more than 50,000 years to leak out and reach us at the Earth. This means that, in fact, the Sun could have shut down tens of thousands of years ago and we would not yet see large effects of the shutdown. Neutrinos, on the other hand, because of their ghost-like nature escape freely from the Sun, taking only around 2 seconds to leak out, and then take only a further 8.3 minutes to reach the Earth. Neutrinos tell us what the Sun is doing now, the light tells us what the Sun was doing tens of thousands of years ago.
If we design an experiment to detect Solar Neutrinos it must then succeed in that it must detect the appropriate number of νs. There is no wiggle-room* (or so we thought in the 1960s).*

Solar Neutrino experiments were started in the 1960s by Brookhaven scientist, Ray Davis (see Section 14.2 How do We Know What is Happening inside the Sun?on Inside the Sun?) to verify that we understood how the Sun worked. No one thought that the experiment would that interesting; it would be difficult but the result would not be surprising. It came as a rude surprise when Davis's experiment detected fewer neutrinos than predicted by the best models of the Sun, throwing doubt onto whether we really did understand our Sun. Follow-up experiments also found ~1/3-1/2 of predicted neutrinos. This conundrum persisted for ~35 years until the early 2000s when, first, the Super-K (Super Kamiokande) experiment showed neutrinos were chamaeleon-like in nature. Neutrinos, once produced, could change into forms undetectable by the early experiments. The SNO (Sudbury Neutrino Observatory) experiment, able to detect transmuted neutrinos, then came online and detected the predicted number of Solar neutrinos. The amusing result was that a simple observation of the Sun led us to a deeper understanding of how the Universe works on the sub-nuclear scale!

Comment: The Davis experiment was a remarkably difficult experiment. The vat contained ~400,000 liters of cleaning fluid (tetrachloroethylene). This vat contains ~2x10³⁰ chlorine atoms. The neutrinos interact with the chlorine (on rare occasions) transforming the chlorine to radioactive argon which is subsequently detected. A huge number of neutrinos passes through the vat every second, 400 billion neutrinos flow through the detector per square inch per second. Remarkably, one expects to build up only a few tens of Argon atoms every month! This exceedingly difficult experiment was performed accurately enough by Davis to show that there were roughly 1/3 the number of neutrinos passing through his experiment as was predicted. This had three primary explanations: (1) Davis was not right: (2) the astronomers were wrong and we did not understand the Sun; or (3) our understanding of neutrinos was not complete.
The Nobel Prize in Physics 2002 was awarded to Raymond Davis Jr. and Masatoshi Koshiba for "pioneering contributions to astrophysics, in particular for the detection of cosmic neutrinos." They shared the prize with Riccardo Giacconi for "pioneering contributions to astrophysics, which have led to the discovery of cosmic X-ray sources." The Nobel Prize in Physics 2015 was awarded to Takaaki Kajita and Arthur B. McDonald for "the discovery of neutrino oscillations, which shows that neutrinos have mass" using Super-K and SNO, respectively.

D. STELLAR-TERRESTRIAL CONNECTIONS

"WE ARE STARDUST": Big Bang, Solar, and Terrestrial Chemical Abundances (17.3)
At left is shown the chemical make-up of the Sun. In terms of the number of atoms, the Sun is ~91 % hydrogen, ~8.9 % helium, and a little bit of everything else. Also, more interestingly, when the Universe began, Big Bang created primarily hydrogen and helium with essentially nothing heavier. How does this compare to the Earth? Well, the chemical abundance of the Earth is grossly different. Most of the elements found in the Earth had to have been at one point in the interior of a star. The heavy elements of which we are made were, for the most part, produced in normal stars and exploding stars known as Supernovas and γ-ray Bursters through fusion reactions.
The Nobel Prize in Physics 1983 was shared by William Alfred Fowler for his pioneering work on the "theoretical and experimental studies of the nuclear reactions of importance in the formation of the chemical elements in the universe." Fowler shared the prize with Subramanyan Chandrasekhar for his "theoretical studies of the physical processes of importance to the structure and evolution of the stars."

Supernovas and γ-Ray Bursters
At left is shown a before and after image of the galaxy UGC 9379 taken from the Palomar Observatory showing a Type IIb Supernova that exploded in 2013. UGC 9379 is a typical spiral galaxy around 360 million light years from the Earth (a light year is the distance a beam of light can travel in one year = 9.46 trillion kilometers). The power of these tremendous explosions can be appreciated by noting that supernova SN 2013cu stood out against the background of rhe galaxy; galaxies are typically made up of 100s of billions of stars! Typical Type II Supernova radiate at rates of 10³⁶ Watts or 10 billion times as luminous as the Sun! Even though distant can such events damage the the Earth's atmosphere? SN 2013cu is much too distant to affect the Earth, but supernovas in our local galaxy, the Milky Way, could offer problems. The potential supernova Betelgeuse is 650 light years from us, around 500,000 times closer than SN 2013cu. The image below left shows that Betelgeuse is currently showing activty. 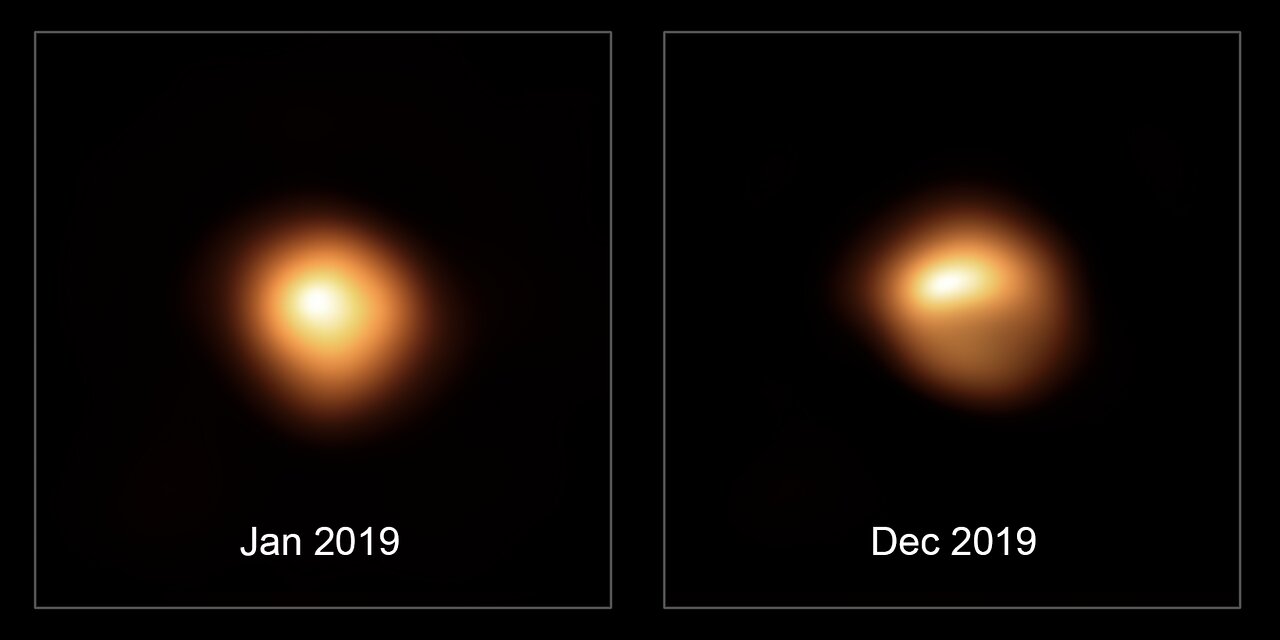Studies show that Betelgeuse is too distant to harm significantly life on Earth (as are any potential supernova); Betelgeuse could cause short-term effects, however, such as depletion of the ozone layer because of its increase ultraviolet luminosity. Astronomers estimate that a supernova must be within 25 light years of the Earth to harm severely the life on Earth. Despite this, Betelgeuse will still put on a spectacular light as it could become brighter than the full Moon in the sky.
γ-ray bursts are sometimes assocaited with supernovas. If one is produced in Betelgeuse's explosion and is pointed toward the Earth, γ-ray bursters are strongly beamed, there could be problems. This is not likely though, because for one it is not clear how likely it is for Betelgeuase to produce a γ-ray burster, and even if it does, it is not likely that the beam will point toward the Earth as the beam is very narrow.