The Solar luminosity is, in principle, easy to find once the Astronomical Unit (A.U.) is known. The Astronomical Unit is the average of the closest distance and greatest distance the Earth assumes as it orbits the Sun. To understand how this done, consider the following.

---

Recall the inverse square law:

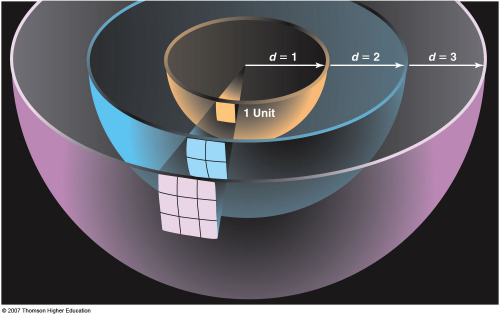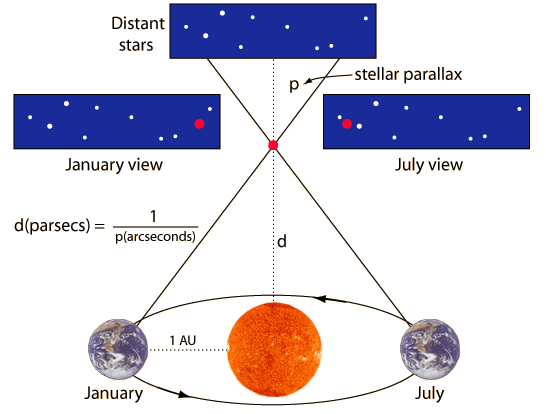
The brightness of the Sun falls off as 1/D2 and so if we know the distance to the Sun we can infer its true brightness from its measured brightness. Seems straightforward enough, are there other problems? The distance to nearby stars can be found through annual trigonometric parallax. Find the angle d. The angle d is tiny, in general. The largest such angles for the closest stars are on the order of 1/3,600-th of 1 degree. This tiny angular unit is known as an arcsecond. If a star has a parallax angle of 1 arcsecond, it is at a distance of 1 parsec = 3.08x1013km = 3.26 light years from the Earth

---

Yes, we need to know the total flux from the Sun or star (which is referred to as the bolometric flux):

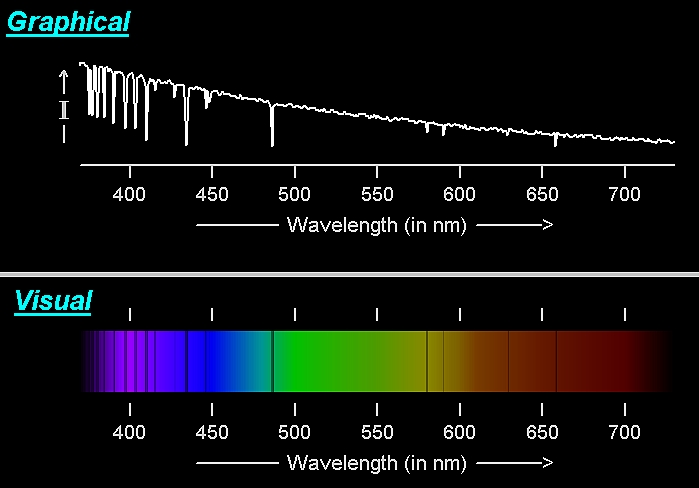
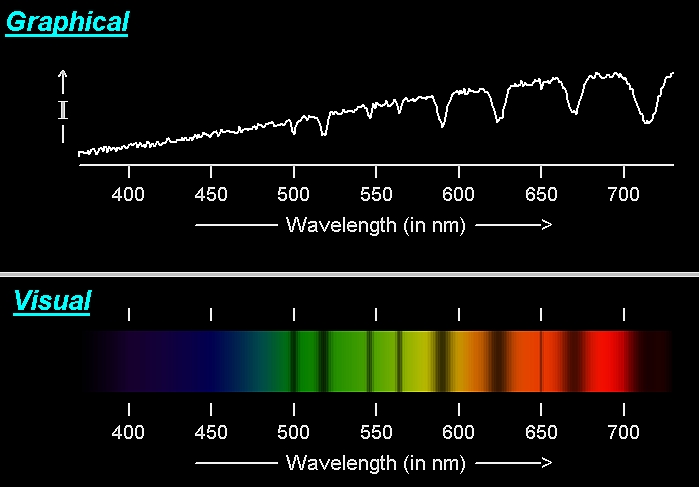
Looking at the hot star on the left, we see that its (Rigel's) spectrum peaks in the UV, outside of the visible band of the spectrum. We need to get above the atmosphere to measure the bulk of its energy. The cool star on the right (Antares) has a spectrum which peaks longward of the optical portion of the spectrum. We need to somehow measure its spectrum out into the IR.

---

The atmosphere of the Earth only allows the visible and radio (plus some bands in other wavelength regions to hit the Earth's surface) and so, in order to measure the bolometric luminosity of the Sun one must send probes above the Earth's atmosphere to measure the Solar spectrum. Once this is done we can then use our knowledge of the Astronomical Unit to infer that the Solar luminosity is 3.84x10²⁶ Watts.

---

This is the way in which other star's luminosities must also be determined. The bolometric flux is always difficult to measure, but the major difficulty is finding accurate distances to stars.