Tying Things Together: Hertzsprung-Russell Diagram, Mass-Luminosity Relation, ....

I. Limited Russell-Vogt Theorem

The properties of a star are determined by its mass and chemical composition

This statement is so powerful that it has been given the name the Russell-Vogt theorem (although it is not a theorem in the mathematical sense). Why the Russell-Vogt theorem in the above form is true will be explained when we talk about stellar structure.

II. Hertzsprung-Russell Diagram (H-R Diagram)

We know the masses, radii, luminosities, and surface temperatures of many stars.
Question: How do we make sense of the plethora of available data?

The first step is to graph the data. The reason we go through this exercise is because plots can indicate whether properties of different stars are correlated, that is, if there is seems to be a physical relationship (connection) between the different properties.

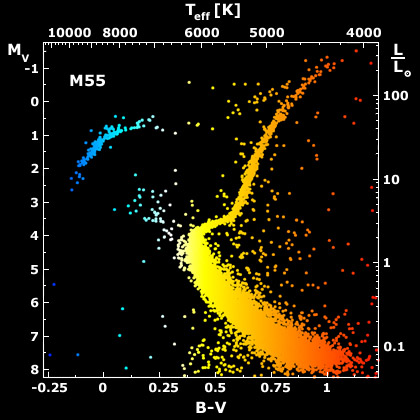
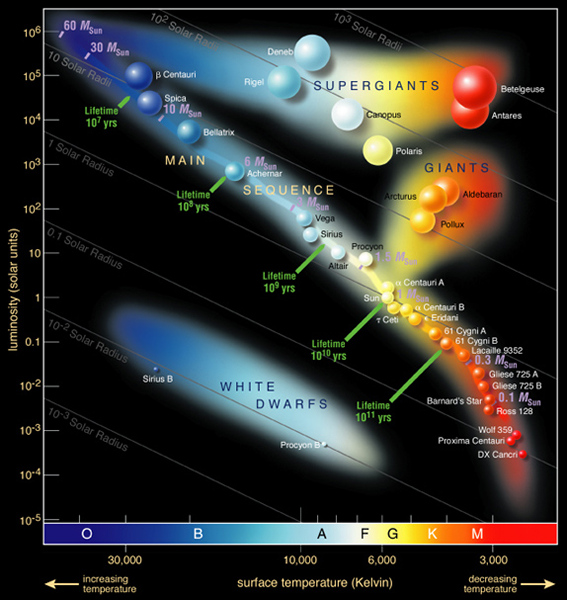
H-R Diagram
In the early 1900's, Ejnar Herstzprung and Henry Norris Russell independently made the discovery that the luminosity of a star is related to its surface temperature. The resulting plot is amazing. A schematic Hertzsprung-Russell diagram is shown to the right. A Hertzsprung-Russell diagram for the old cluster M55 (Mochejska & Kaluzny, see APOD, 2001 Feb 23) is the top panel on this page. The Hertzsprung-Russell (HR) diagram was one of the most important astronomical discoveries of the twentieth century.
Hertzsprung and Russell used the spectral class (which is related to the temperature, and color of the star [which is related to B-V]) in their plots. They ordered the stars as O, B, A, F, G, K, and M. Since O stars are the hottest stars, this means that the temperature axis in the HR diagram is odd in that the temperature decreases as one moves to the right. The veritcal axis is the luminosity of the star, it increases upward. The axis is logarithmic (it mimics the human eye).

Stars are confined to specific regions in the HR diagram. This tells you that there is some physical relationship between the luminosity and temperature of a star. To make this point clear, let's look at people. People have many defining characteristics, not all of which are related. Let's plot some properties of people and see what they look like. Consider,

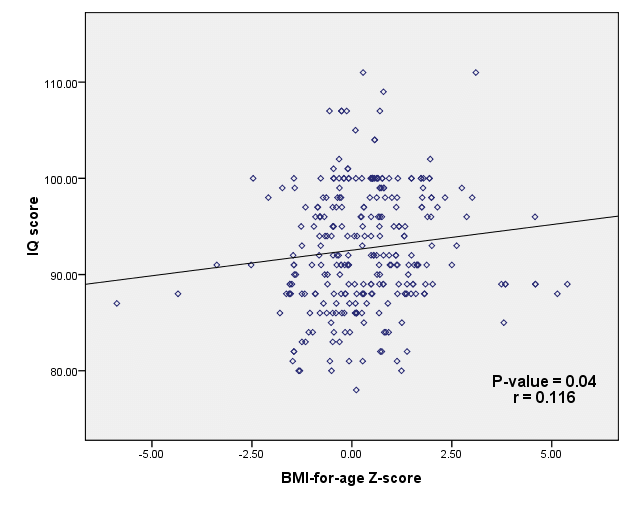3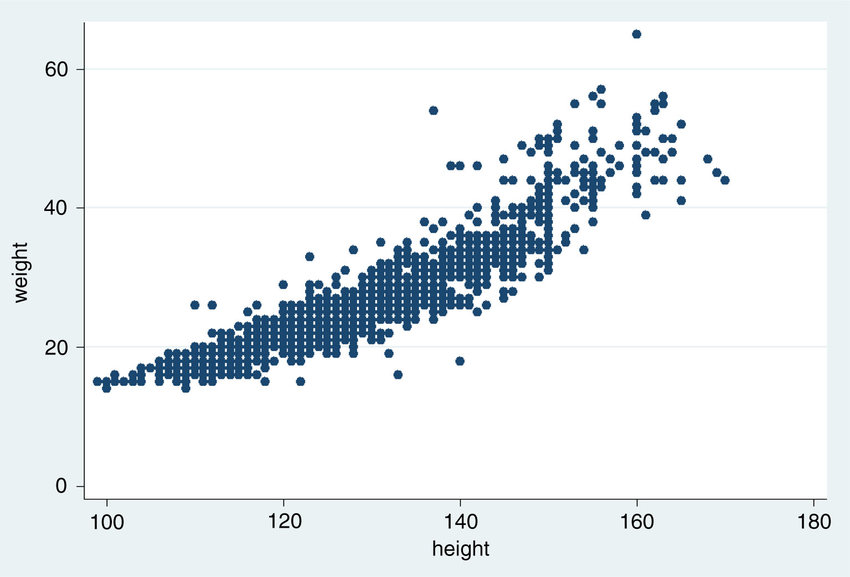

The plot of IQ versus BMI is essentially a scatter diagram ===> there isn't a physical relationship between IQ and BMI.

The plot of weight versus height for a sample of people shows a correlation ===> that there is something in the structure of people which makes weight and height correlated.

This simple exercise taught us something about people. We did not learn in detail how people are put together; we learned that the height and weight of people are somehow related. It is up to theorists to explain the how and why of the physical connection between the height and weight of the people population.
Similarly, the HR diagram is not telling us about how stars are put together. It is, again, up to the theorists to tell us what is going on. However, for now, let's ignore the role of the theorist and just examine the HR diagram to see what we can deduce about stars.

III. Inferences Based on the Hertzsprung-Russell Diagram

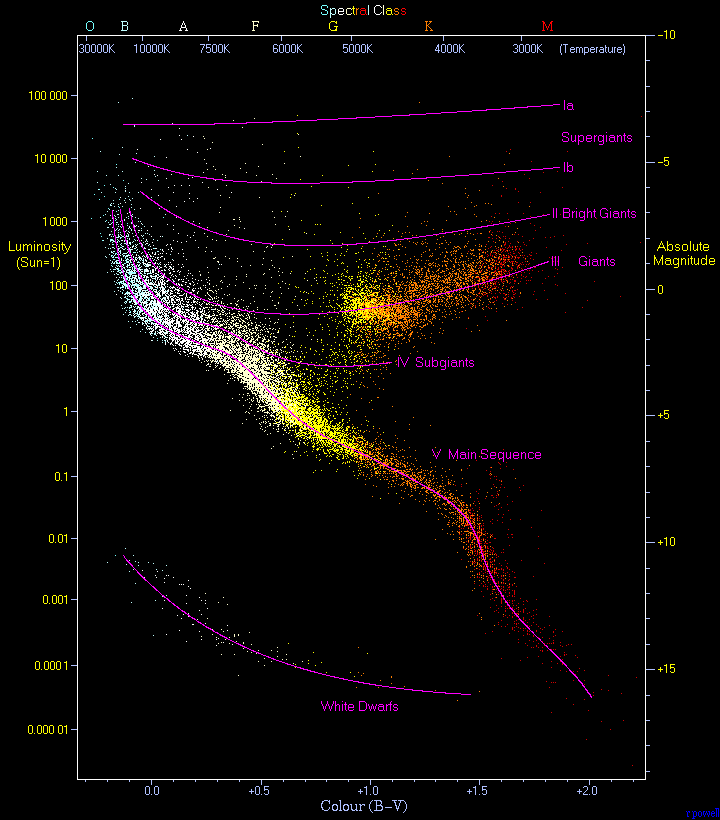
Luminosity Classes
I -- Super-Giants
II -- Bright Giants
III -- Normal Giants
IV -- Sub-Giants
V -- Main Sequence Stars

Question: What can we deduce from the HR diagram?

Let's address the names of the different groupings of stars, i.e., Main Sequence, Giants, Super-Giants, and White Dwarfs. These groups are referred to as Luminosity Classes. Without having actually measured the radii of all of these stars,
Question: How did we know that the stars in the upper right hand corner of the diagram were big, while the stars in the lower left hand corner were small? (from Stefan-Blotzmann Law)

Given a random sample of stars, we find that roughly 85-90 % of the stars fall along the Main Sequence and that the bulk of the other stars are White Dwarfs with < 1 % Supergiant and Giant stars .

Question: What does the relative numbers of stars in these groupings tell us about how long stars spend in the different Luminosity Classes, the Main Sequence stars, Supergiant and Giant stars, white dwarf stars, and so on?

The percentages tell us the fractions of the lifetimes stars spend in each of the Luminosity Classes
We also find out that stars do not evolve significantly while on the Main Sequence (stars do evolve as shown by the Sun, but not significantly). That is, O stars are found to be massive with the masses up to 50-100 times the mass of the Sun. The masses of the stars fall as one moves along the Main Sequence. The lowest mass stars are the M stars whose lowest masses as 10 % that of the Sun. See the Table below.

Main Sequence Stars

Roughly, along the Main Sequence stars have properties:

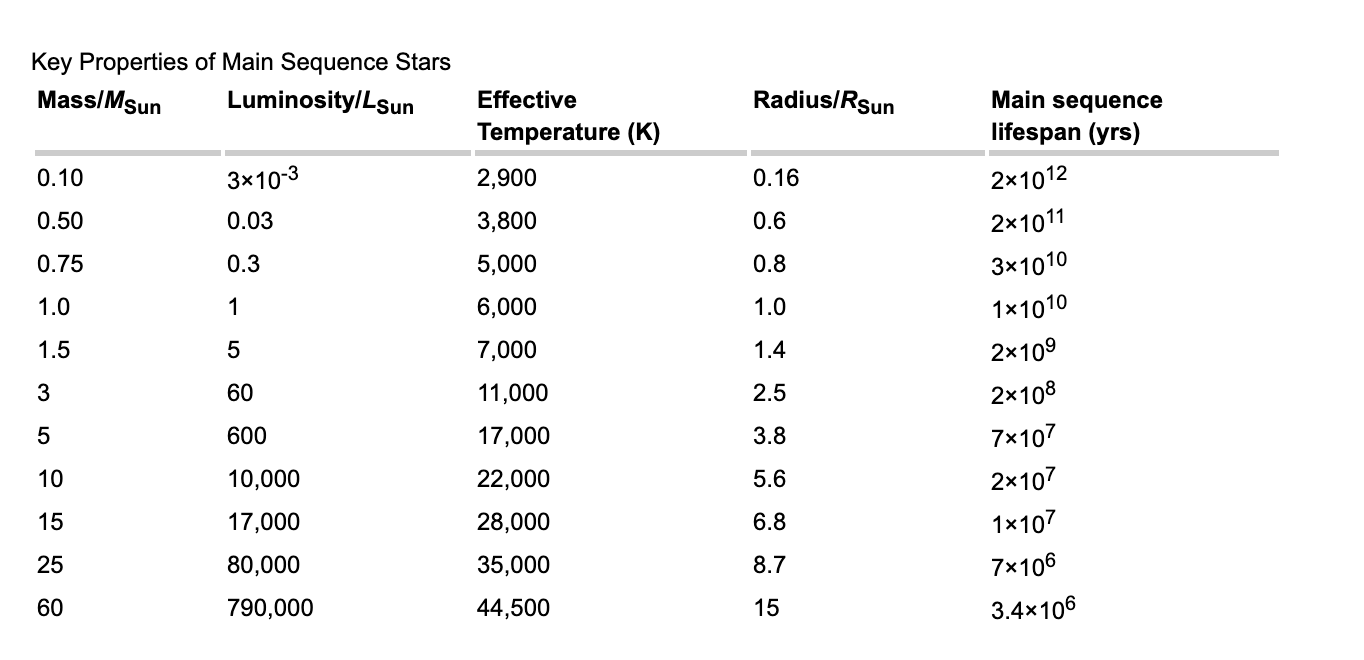
In the following boxes, we show simple relationships between the stellar properties, the luminosity, radius, effective temperature, and the mass of the star.

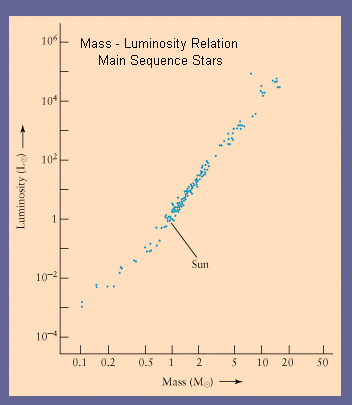Mass-Luminosity Relation for Main Sequence Stars

When we consider Main Sequence stars, is there any hint about whether an individual star evolves along the Main Sequence or whether a star once on the Main Sequence does not change its position? We believe that stars do not move along the Main Sequence. That is, Main Sequence stars with particular L have the same properties. This can be seen from the Mass-Luminosity relationship for Main Sequence stars where stars with a given mass M, have a well-defined brightness, L.
The result shows that the upper end of the Main Sequence (the most luminous stars) is occupied by massives stars and the lower end of the Main Sequence (the faintest stars) is occupied by the least massive stars.
For stars more massive than around 0.7 solar masses, L ∝ M⁴ and for less massive strs, L ∝ M³. Because we know that Main Sequence are characterized as stars that get their energy from fusion reactions that convert hydrogen into helium in their cores, we may infer how long Main Sequence stars live from
Lifetime = (Amount of Available Fuel)/(Rate Fuel is Burned) = (M_c²/L)
Using the M-L relationhips, we see that

Lifetime ∼ 10 (M_/M_Sun)^-3 billion years for massive stars, and
Lifetime ∼ 200 (M_/0.5 M_Sun)^-2 billion years for low mass stars.

Interestingly, stars whose masses are a little less than that of the Sun have such long lifetimes that they have not yet had time to run through their Main Sequence lifetimes since the start of the Universe 13.8 billion years ago!

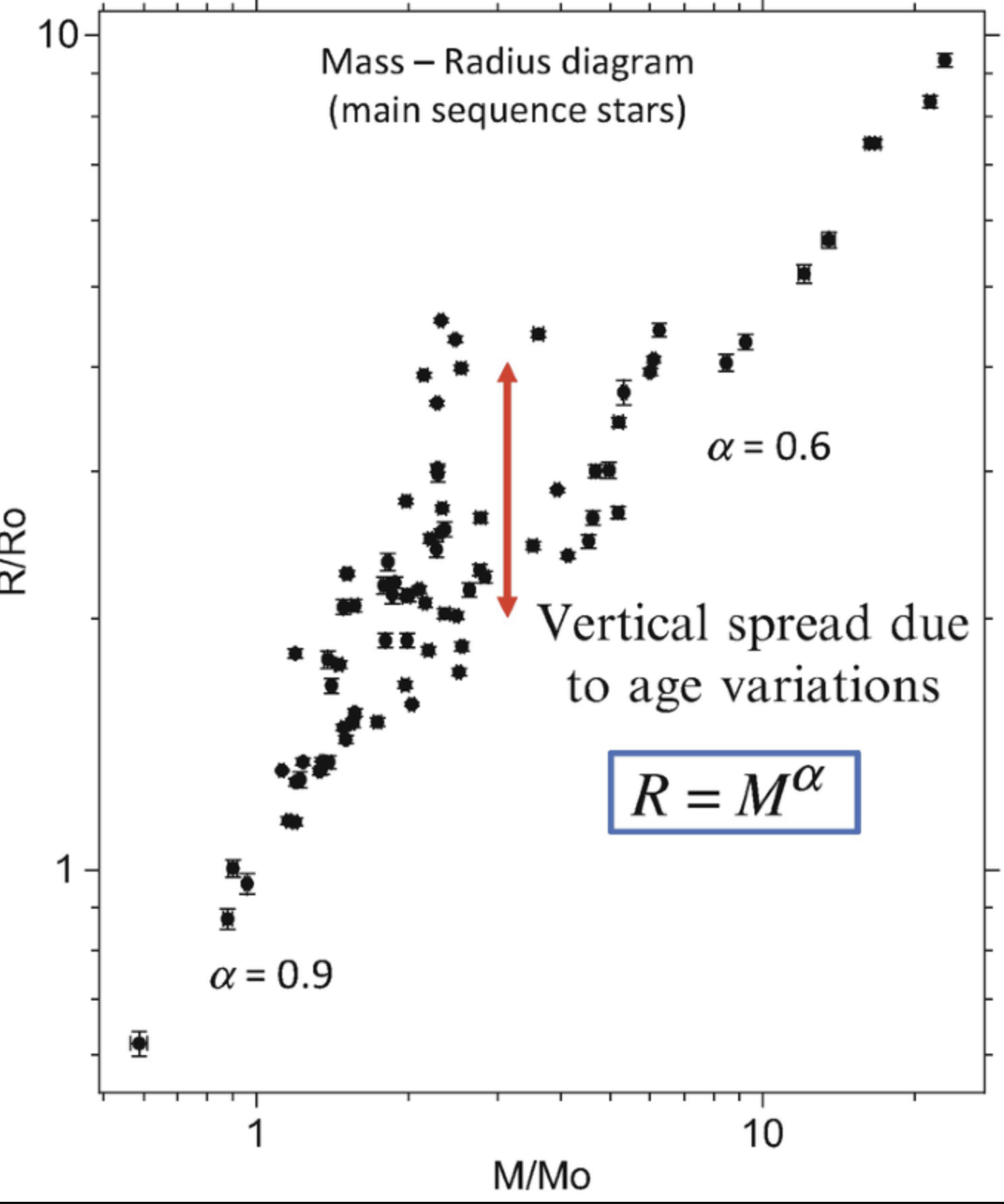
Mass-Radius Relation for Main Sequence Stars
The size (radius) of Main Sequence stars increases with increasing stellar mass as does the luminosity. The figure shown to the indicates roughly how the size increases with mass. We see an interesting result for Main Sequence stars which is that stars become less compact (less dense) with increasing stellar mass. That is, as you go to the low temperature-low luminosity end of the Main Sequence, the density of the stars actually increases.
The increase of the stellar density (how compact are the stars) with decreasing stellar mass tells us a lot (as we will show when discuss star formation). In particular, this tells us us why there is a lower limit on the mass of Main Sequence* stars.

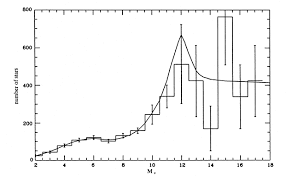
Luminosity Function

In terms of mass, stsrs are not distriubted evenly along the Main Sequence. distributed smoothly. There are many more low luminosity stars than there are high luminosity stars. A plot of this distribution is known to as the Luminosity Function. The plot for the left area around the Sun, the Solar Neighborhood, but it is representative of stars in our Galaxy. Note that for stars the luminosity of our Sun (in Absolute Magnitudes, M_V ~ 5). Based on this figure there are around 4 stars every 10³cubic light years in the Solar Neighborhood. That is, there is one Sun-like star in every cube whose sides are 10 light years long. Sun-like stars are roughly 10 to 30 light years apart in the Solar Neighborhood. The number of stars increases strongly with decreasing luminosity. We find stars around 1 % the luminosity of the Sun, are much more common, separated by distances of around 1 light years or so.