Dynamical Tests

Weighing the Universe

There are obvious contributions to the density of the Universe, e.g., planets, galaxies, ... , however, there are also other not so obvious contributions. We need

total mass density = baryons + neutrinos + photons + ...

Using the above, we define

So the issue becomes what are all of these contributions to Omega?

Before we go on, photons are in there, but why? Aren't photons massless? And what if neutrinos turn out to be massless? Why are they there?

Galactic Masses (Individuals and Groups)

I will discuss galaxies as probes of the mass of the Universe. In some cases, there will be direct counting of galaxies, in other cases, the galaxies will be used as test particles. Define

We will measure Omega(galaxy) using light and dynamical techniques

Light Method

This is straight-forward. We simply count up galaxies. The complication is that we observe primarily the galaxies which are easy to see. However, there are also many galaxies which are hard to see. These hard to see galaxies are the ones with low surface brightness (which means that they are very hard to see against the pervasive background of the night sky. The number of these low surface brightness galaxies is not yet well-established, however, the current density distribution of galaxies is interesting. But anyway, let's press onward under the assumption that we may be making a factor of 2 error or so by only considering the bright galaxies in our discussion.

Recall, galaxies are divided up into different types:

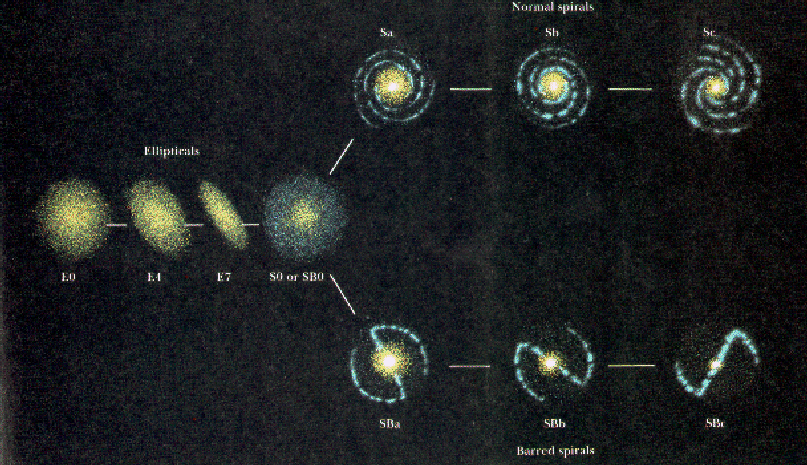
The different types of galaxies have different Mass-to-Light (M/L) ratios. To get a feel for what M/L tells us, consider: The Mass-to-Light ratio depends on the types of stars that populate galaxies and how much unseen matter exists in the galaxies.

The typical M/L for the visible parts of galaxies are:

===> Omega(gal,visible) ~ 0.007 (factor of 2 uncertainty) << 1

Dynamical Methods

The dynamical methods are indirect in the sense that you do not count-up things. You rely on Newton's laws of physics and gravity. The dynamical methods are applied on all scales -- from individual galaxies to pairs of galaxies to clusters of galaxies to clusters of clusters of galaxies to ... .

GALAXY ROTATION CURVES (1970's)

Consider individual disk galaxies. Recall the discussion of the Tully-Fisher method. We imagine the stars and the gas in the disks of spiral galaxies are in orbit about the centers of the disk. In this case, we have that

M(galaxy) = Rv2/G

So, if we say, pick out a star and then measure how far it is from the center of the galaxy and how fast it is moving ===> mass contained within the orbit of the star (if the mass of the galaxy is distributed spherically). This is a powerful method, for example,

This is a nice way to measure the masses of galaxies. However, let's look at the rotation curves of some other galaxies. The curves are flat at large radii. Based upon rotation curves, one concludes that the dark matter in the halos contributes at least 3 - 10 times the mass density of the luminous parts of the galaxies ===> Omega > 0.02 --> 0.07

BINARY GALAXIES

For two galaxies in orbit, M/L ~ 90 with an error of 40. Results aren't too good, but we note that M/L is still >> the M/L for the luminous parts of galaxies.

CLUSTERS OF GALAXIES (1930s)

For one galaxy (roughly speaking), its motion is like orbital motion and we can infer the mass of the entire cluster of galaxies. Result:

M(total) ~ v2 {average R} / G ===> Omega(cluster) ~ 0.1 - 0.3

Peculiar Motions

The techinques about which I've talked, lead to Omega < 1.

LENGTH SCALES

The Cosmological Principle says that the Universe is homogeneous and isotropic on some appropriately large length scale. This means that if we divide the Universe into large boxes and then mix up (smooth) the contents of the boxes, the set of smeared out chunks of the Universe will make a smooth Universe which appears homogeneous and isotropic to all observers in the Universe.

It is apparent that on small scales the Universe is not isotropic and homogeneous, e.g., the Solar System is clearly lumpy. Thus, the question is On what scale does the Universe become smooth?, because it is on this scale and larger that we measure the average density of the Universe.

So far all of the measurements of the mass (density) of the Universe have relied on galaxies. Our measurements are thus local in that we measure the mass of the Universe where we can easily see mass. What are the consequences of this procedure?

  • Galaxies: M ~ 1011 M(Sun) and R ~ 50,000 light years ===> rho(gal) ~ 4 x 10-25 gm per cubic centimeter >> rho(crit)

    Does this mean that the Universe is closed? No. The galaxy is a very overdense region of the Universe and we need to average over a larger box. The Milky Way resides in the Local Group where the large galaxies are separated by around 10 million light years. What is the density of material when smeared out over this larger volume?

    rho(Local Group) ~ 5 x 10-32 gm per c.c. << rho(crit) as claimed!

    The problem is, is the space between galaxies really empty?

  • Clusters of Galaxies: M ~ 1015 M(Sun) and R ~ 10 Mly ===> rho(cluster) ~ 6 x 10-28 >> rho(crit), and clusters of galaxies are still not large enough to make us feel confident that we are measuring the average mass of the Universe.

    clusters are separated by ~ 30 Mly (or so) ===> rho(cluster of cluster) ~ 2 x 10-29 on the order of rho(crit).

If we start measuring the mass of the Universe on length scales on the order of clusters of clusters of galaxies or greater, then maybe we can start to feel fairly confident that we are actually measuring the average mass of the Universe and not simply the mass of the overdense parts.

MASS ESTIMATES BASED ON LARGE LENGTH SCALE ESTIMATES

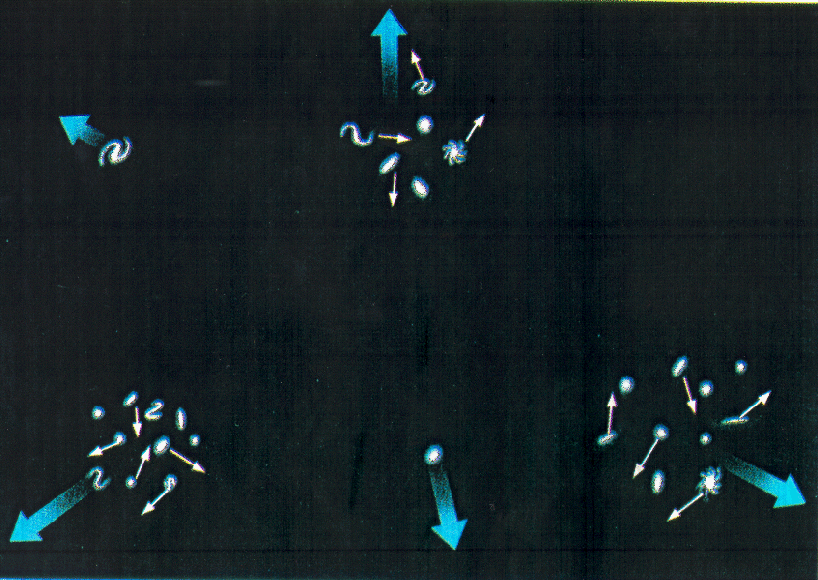
Peculiar Velocities

The overall Universe participates in the expansion, the Hubble flow, shown in the right panel. However, superimposed on the uniform expansion are smaller scale motions due to interactions between galaxies, clusters of galaxies, .... . These motions are referred to as peculiar velocities, streaming motions, ... . This is shown as the internal motions of the galaxies in the figure.

The significance of the peculiar velocities is that in order for them to have persisted over the lifetime of the Universe, they must be driven by something. If they were not being driven then they would have decayed away. The simplest explanation is that there are mass concentrations in the Universe which causes material to move around. For example, consider the

Anisotropy in the CMBR

Anisotropy is naturally interpreted as due to a peculiar velocity of the Milky Way galaxy. The motion has a speed of 600 kilometers per second in the direction of the Hydra-Centaurus supercluster on the sky.

Further (controversial) work showed that the Hydra-Centaurus cluster was also moving in the same direction at 800 kilometers per second and that more distant objects were actually approaching the same point. How did they know this? Well, consider the following Hubble plot. At d < D, the galaxies appear to have higher velocities than the Hubble relation. For d > D, the galaxies appear to have lower velocities than suggested by the Hubble relation.

How can we interpret this result? Well, imagine that there is a large mass concentration at D (the so-called, Great Attractor). This mass will then pull nearby objects toward it. So, things with d < D, will have enhanced velocities and objects with d > D will have decreased velocities compared to their Hubble flow values. More recent results have, however, shown that although we are pulled toward the Great Attractor, we, as well as the Great Attractor are also pulled toward the Shapley Supercluster. Our peculiar motion is thus driven by both the Great Attractor and the Shapley supercluster. This more recent result suggested that the Great Attractor's mass was less than originally estimated.

Results: G.A. at 130 Mly and M(GA) ~ 1016 M(Sun).

  • Estimates of Omega from Peculiar Velocities

    The peculiar velocities are due to mass concentrations which pull on things causing deviations from the Hubble flow. It is clear that the size of the perturbation (the size of the peculiar velocities) will depend upon how much mass pulls on the object. Detailed studies suggests Omega ~ 1.

    Gravitational Lenses

    Due to the curvature of space caused by concentrations of mass, light-rays bend as they pass by stars, galaxies, cluster of galaxies, ... . The bending makes masses act like lenses. A recent release from the HST of a lens produced by Abell 2218. The amount of bend is determined by the mass of the lensing object.

    Abell 1689 (shown to the left), lenses background objects. The HST's Advanced Camera for Surveys found that Abell 1689 lenses 34 different background objects. Redshifts provide distances for 24 of the objects. Using a model for Abell 1689, researchers matched the pictures to predictions made by models for the Universe that included our best guesses for how things work (see WMAP analysis of the CMBR). Assuming a flat Universe and cold, dark matter, the researchers found Omega about 0.3 and the cosmological constant about 1 with somewhat large uncertainties. They found at a 99 % confidence level, that the matter density is between 0.23 and 0.33, consistent with the WMAP results.

    Return to the Expansion of the Universe