
|
|

|
|
expansion velocities (Hubble flow) ===> Cosmological Redshift |

local motions (peculiar velocities) ===> Doppler Shifts |
For slow expansion speeds, z ~ v/c or v ~ cz (as is sometimes plotted when showing the Hubble law).
Recall that the relationship is linear (at least for nearby galaxies), Hubble's Law, where
The measurement of the redshifts to galaxies is straightforward and relatively easy to do. The major uncertainty in determining the Hubble relationship comes from problems in determining the distances to galaxies. We now consider this issue.
This is such an important problem that the Hubble Space Telescope (HST) made the determination of the distance scale one of its principal goals. The usual way in which distances are found is compare the apparent brightness of an object to its true brightness. This technique relies on the inverse square law and knowing the intrinsic brightness of the object observed. Objects for which the intrinisic brightnesses are known are referred to as standard candles. The distance follows naturally from the observed brightness of an object from the relation:

The problem is that there is no single standard candle, an object for which we know its true brightness, which is found in systems close to us and far from us and has a large enough luminosity L to be seen at the ends of the Universe. Consequently, different standard candles must be used to find distances in different regimes. Each successively brighter standard candle is used to calibrate the next brighter one forming the Distance Ladder,
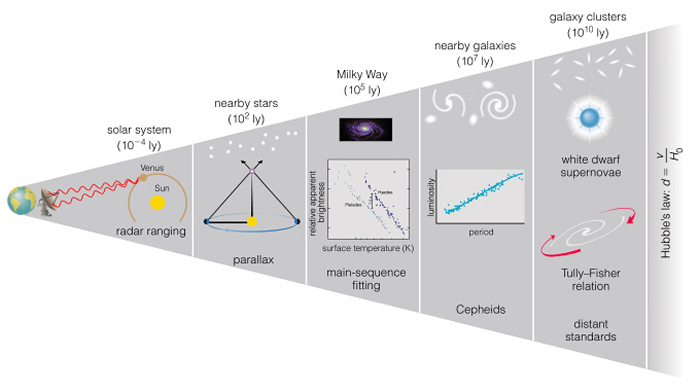
A problem with bootstrapping methods is that since each successive step is built on the previous step, the error in the method grows with each step and the method may become unreliable. For most extra-galactic things, people use Cepheid variable stars (light curve) to start the bootstrapping, i.e., Cepheid variables are considered to be primary distance indicators . Note that this assumes that we know the intrinsic luminosities of Cepheid variables. The pulsation periods of Cepheid variables are strongly correlated with their average luminosities in the sense that the longer their pulsation periods, the brighter they are on average. The Cepheid luminosities are calibrated in the first few steps of the above chain, i.e., distance to Sun (Astronomical Unit) ===> distances to nearby low mass stars via parallax ===> observations of star clusters (Main Sequence Fitting, Moving Cluster Method) which contain low mass stars yield distances to the clusters (===> can infer the distances and hence luminosities of the bright stars in the cluster and thankfully many clusters contain Cepheid variables).
Typical extra-galactic distance ladders are
Milky Way -----> 12 M l.y. ------> 80 M l.y. ---------> 300 M l.y. ---------> 5 B l.y.
Cepheids large HII regions, Galaxy methods (types, Type Ia SN,
brightest stars n-th brightest galaxy in
a cluster, ... )
------------------------------------------------->
Tully-Fisher Method
Interestingly, results based on different chains yield different answers for
Ho ===> different ages for the Universe. For example, Cepheids
go from nearby galaxies to the Virgo cluster,
-----------------> 50 M l.y.
Virgo cluster of galaxies
Cepheids
Even by Virgo, the different methods gave distance estimates which differed by around a factor of 2. HST observed Cepheids in M100 (see Homework 1), a galaxy in the nearby Virgo cluster of galaxies, and re-calibrated the Tully-Fisher method. The HST results suggest that
 |
===> the critical density is ~ 10-29 grams per cubic centimeter |