|
WORLD VIEWS OF THE UNIVERSE
|

|
Cosmological Facts
- Redshift-distance relation, Hubble Law (interpreted as expansion of the Universe) → Big Bang
- Prediction: Cosmic Microwave Background
- Prediction: Hydrogen/Helium abundances
Models of the Universe
Based on Hubble's law and the CMB, our world view of the Universe is rather
firm. On the assumption that Hubble's Law, cz = HoD, is due
to expansion of the Universe and that the Cosmological
Principle is valid, models for the Universe have been constructed
based on Einstein's General Theory of Relativity
.
Einstein himself made models for the Universe (circa
1910-1920s). Unfortunately, he errored because he
believed in a homogeneous, isotropic, and
static Universe (on philosphical grounds).

Hubble Ultra-Deep Field Image |
Wait, recall that the Cosmological Principle
says that the Universe is homogeneous and isotropic for any observer
in the Universe. The appearance of the Universe can change with time, but
all observers must see the same Universe for any given time.
How is this consistent with the observed structure in
the Universe (structures more than 1 billion light years in size!)?
Despite the impressive sizes of these features
(e.g., the
Voids, and the Sloan Great Wall
--1.37 Billion light years across), these
structures are still less than 10 % of the distances to the farthest QSOs
(z ~ 6 ==> more than 25 billion light years away)
and thus fill less than 1 % of the volume of the Universe.
The Universe appears fairly bland on scales larger than these
observed features and the Cosmological Principle seems to hold for our
Universe.
|

Sloan Great Wall |
I. Modern View of the Universe
 |
 |
 |
 |
Outdated Types of Universes |
 |
 |
 |
 |
After Einstein
developed his General Theory of Relativity,
Alexander Friedman and
Georges Lemaitre developed
the first models for the structure
of universes based on Einstein's
General Theory of
Relativity. Lemaitre
was the first to suggest that the
Universe came from an initial dense state, the
primeval atom and is said to be
the father of the big bang. The term, Big Bang
, was
coined later by Sir Fred Hoyle
in an attempt to mock the idea.
Using General Relativity and assuming that
the Cosmological Principle
was valid for our Universe, Friedman found
three types of evolving universes.
To get a feel for Friedman's
models, we will usually demonstrate properties
of Friedman universes
using two-dimensional examples even
though we know that our Universe is actually at least
four-dimensional in nature. Four-dimensional?
We know length,
heighth, and width, that is, there are three-dimensions for things
in our Universe. What is the fourth
dimension? That is, what is the fourth thing we must specify
in order to describe locations in our Universe?
Spacetime:
In general, to specify
events in our Universe we must tell you: (1) where the event takes place
(the spatial location of the event);
and (2) when the event takes place (the temporal location of the event).
So, to specify an events in a universe
→ we must consider
universes to have four dimensions, the 3 spatial locations and
the time
of an event. These define the spacetime coordinates of an event.
Note that in our Universe, although
time is in a sense a simple coordinate
equivalent to position, time
seems to occupy a preferred place in our Universe in that we can
move arbitrarily through space but we cannot
seem to move arbitrarily through time.
|
Interestingly, the framework upon which we
place these spacetime events
for the Universe can have different shapes and that the shapes can be
modified by the presence of mass and energy. This is completely contrary
to Newton who thought that space was rigid and that there was a master
clock in the Universe which kept time for everyone.
These notions are interesting because the way objects move is determined by
the shape of spacetime, objects simply follow the lay of the land
as they move. The way mass and energy fit into this idea is that mass and
energy are able to distort the shape of spacetime. Mass and energy tell space
how to bend. Spacetime then tells mass and energy how to move.
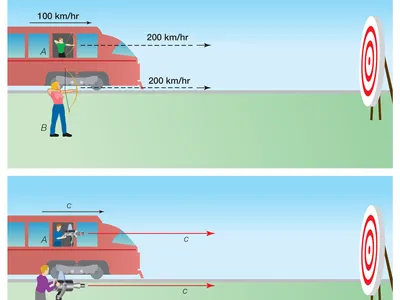
(a) At slow speeds, velocities simply add (top panel). In the picture, the
arrow hits the target at speed = 300 km per hour for the arrow fired from
the train while the arrow hits the target at speed = 200 km per hour for the
arrow fired the person on the ground. (b) At high speeds,
the speed an observer sees is limited by the speed of light (bottom panel).
In the picture,
the beam of light hits the target traveling at speed c, the speed of light,
for both the beam fired the train and the beam fired from the
ground. This is odd as the person on the train sees the beam of light
leave him traveling at the speed of light c!
This happenstance occurs because
moving clocks run more slowly than stationary clocks. |
 The star
distorts the shape of specetime. The moving ball simply follows the
shape of spacetime. This is the ball's natural motion, it feels no force.
Matter curves spacetime; spacetime tells matter
how to move.
|
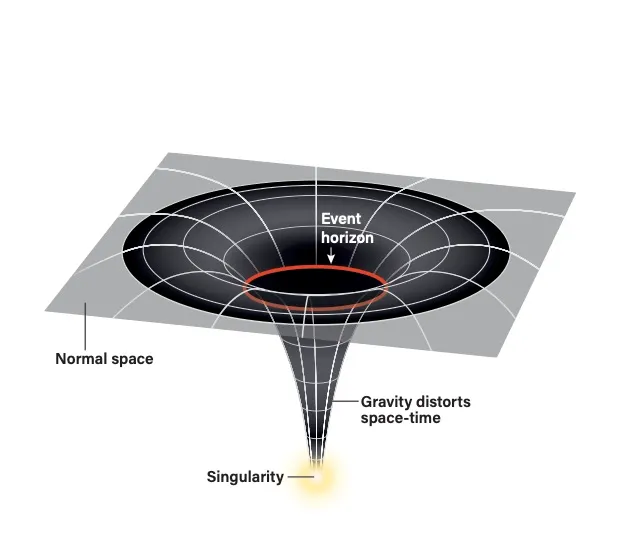
Example: Black Hole |
Modeling of a black hole requires Einstein's
GR, however, the idea behind them is simple. Black holes were predicted in
the 1700s by Michell and Laplace who envisioned objects
referred to as Dark Stars.
A nonrotating black hole is shown to the left. The mass of the black hole
resides in its center,
the Singularity
where matter is compressed to infinite density. The radius where the
escape speed from the mass is equal to the speed of light, c,
is marked by the Event Horizon.
The Event Horizon is not a
solid surface. This radius is the
Schwarzschild Radius.
Clocks run more slowly in the vicinity of the
Event Horizon. Inside of the
Event Horizon, an object would have to
travel faster than the speed of the light to escape
→ even light cannot escape and
the name Black Hole.
Falling into a Schwarzshild Black Hole
(for further information, see
see A.J.S. Hamilton [JILA])
Some Things about Black Holes
- Black Holes Have No Hair
A black hole is characterized by its mass, its spin, and its electric
charge
- Cosmic Censorship
Singularities are cloaked by Event Horizons
(no naked singularities)
|
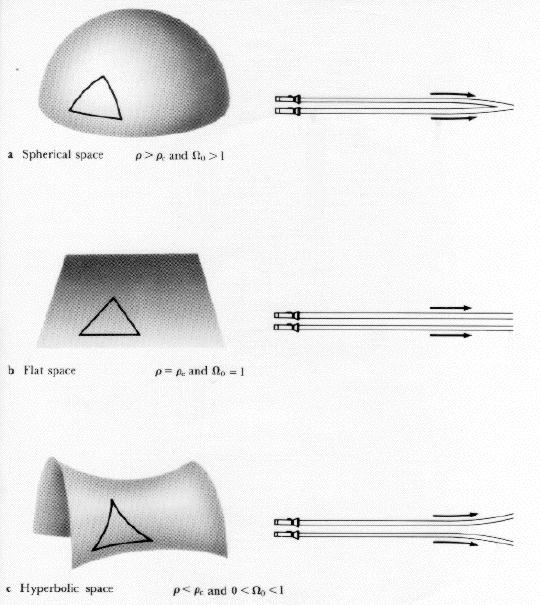
In terms of spacetime, the Friedman models are
flat (Euclidean space, critical universe),
positive curvature (e.g.,
a sphere, the closed universe), and
negative curvature (e.g., a saddle, open universe)
universes. In two-dimensions, positive and negative curvature spacetimes
look like
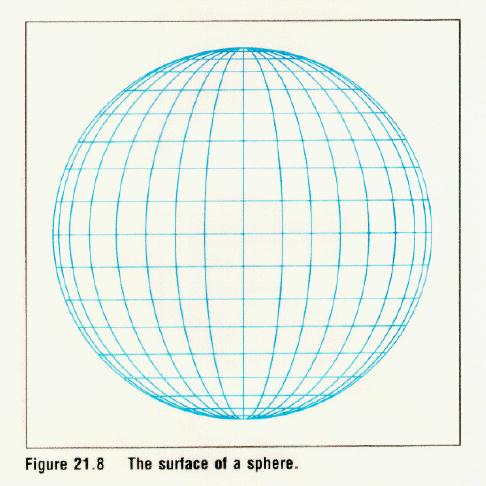
positive curvature |

negative curvature |
Abstract as are these concepts, these shapes
(topologies) have important consequences for how our Universe evolves,
the ultimate fates of the Universe.
If we can determine the topology
(geometry or shape) and composition of our Universe
then we can infer what is going to
happen to our Universe
in the distant future. In the coming weeks, we explore how astronomers
deduce the shape (topology) and composition of our Universe and thus
determine the ultimate fate of our Universe.
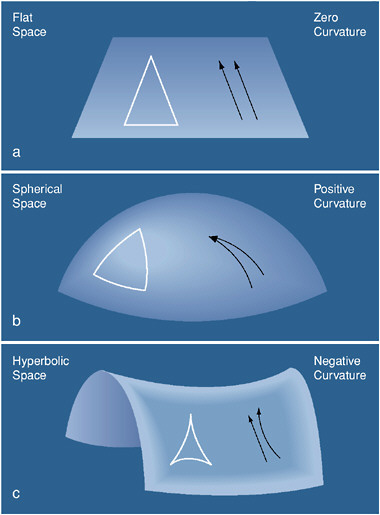
| Properties of Geometric Objects in Different
Universes
The geometry (curvature) of each type of universe is different; the
spacetime
of each universe has different character. Simple measurable differences
between the universes can be found from properties of different geometric shapes
and features in each spacetime.
Triangles, parallel lines, circumferences of circles behave differently in
the different universes (see the left panel).
|
II.
The Fate of the Universe
A great deal of effort is now directed toward determining which of
the above models is the correct one for our Universe. How can we go about
this exercise. Well, initially,
the Universe was driven to expand by some unknown impetus. The
current rate at which the Universe expands is measured by the
Hubble
constant Ho. The expansion is slowed by the gravitational
attraction of material contained in the Universe. If the amount of material
is large enough then the expansion of the Universe will be halted
and the Universe will eventually stop expanding and start to contract!
In this sense, we can define
an escape speed for the Universe. If the Universe
does not exceed this escape speed,
it will reach a maximum size and collapse.
Hubble Law and Topology of the Universe
How does the Hubble Law, that is, the relation between the redshift of
and distance to far-away galaxies behave and how is it interpreted
in the context of Einstein's General Theory of Relativity
and the different Friedman models.
The different Friedman models for universes can only be differentiated
by how the Hubble Law behaves at large distances.
When we see an object, we see the object as it
was in the past. We do not see the object it is now! If an object is
at a distance of 1 million light years, we see the object as it was
1 million years ago! So when we see an object at large distance, we see the
object as it was when it was younger and by the same token, we see the
Universe as it was when it was younger
(as it was in the past).
In this way, we may be able to differentiate between the different
Friedman model (open, closed, and flat). |
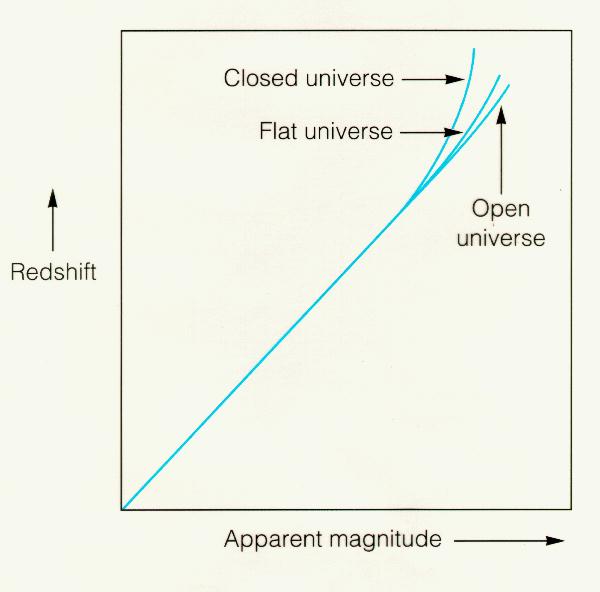
|
Comment: There is then some critical amount
of material in the Universe (which determines how strongly gravity slows the
expansion). For this precise amount of stuff,
the Universe assumes a critical form
where it is neither open nor closed,
but is
flat. This amount of material leads to the definition
of the Critical Density.
The Critical Density
is the amount of material the Universe must contain in order
to be flat. The critical
density depends on
how fast the Universe expands.
The faster the Universe expands the larger is the
critical density.
For the currently
accepted Hubble constant, Ho ~ 73
km per second per
Mpc, the critical density
is around 9x10-27 kg per cubic meter or around 6 hydrogen
atoms per cubic meter.
This is tiny, the density of air in this room is around
1.2 kg per cubic meter.
As a measure of how close we are to this critical density, we define
Ω (the
Greek letter Omega),
Ωo = (average density)/(critical density)o
In a
flat Universe, we then have
Ωm+ΩΛ = 1
where the density is composed of two parts, the matter density, the
dark matter and the normal
matter, and the Dark Energy component.
The flat universe is the dividing line between
open and
closed universes and is an
unstable solution.
If the universe has
Ωm+ΩΛ < 1,
then the universe is open.
If the universe has
Ωm+ΩΛ > 1,
then the universe is closed.
Currently, WMAP has made the best measurement of
Ω
finding Ω =
1.02±0.02, a result consistent with 1.
This result is puzzling because, if at its beginning, the Universe was
nearly flat but not quite flat,
it would have evolved
quickly to either a rapidly expanding open universe
or a rapidly collapsing closed universe.
For our Universe to be as old as it is and so nearly
flat means that in the
beginning, the Universe must have had Ω = 1 to 60 digits.
Why would the Universe find itself with this one precise condition from
the plethora of other possibilities (anything other than 1!).
This is the
Flatness Problem
|
Scale Factor, R(t)
Properties of the different Friedman solutions can be
readily visualized using another type of plot, one
where we plot what is referred
to as the scale factor
for the universe, R(t) as a function of time.
The scale factor,
R(t),
tells us how much bigger or smaller the Universe is today than
it was yesterday and so on.
- Scale Factor → Size = R(t) x Size (in the past)
where Size (in the past) is often times chosen to be the size of the
Universe today.
In terms of R(t),
Friedman solutions for the evolution of the universe
are shown to the right. The Flat universe
that contains only matter, the
green curve,
stops expanding after an infinite amount of
time has passed. The Flat universe
dominated by dark
energy, the curve continues to expand
even after an infinite amount of time has elapsed. Open
universes also never stop expanding even if they do not contain
dark energy.
A closed universe,
is shown by the bottom curve.
|

|
III.
The Fate of the Universe
The determination of
the ultimate fate of the Universe is a
major goal of cosmology and will be addressed in later
classes, Topic 4.
The methods used
to determine the appropriate universe model fall into three categories:
- Dynamical Tests
where we look at how fast the Universe is expanding
as measured by the Hubble constant, Ho, and compare it to the
amount of mass, radiation, and dark energy in the Universe
- Topological Tests
where we try and determine the shape
of the Universe directly
- Passive Tests
where we match
our most promising models to detailed observations of the Universe.
In particular, we see which model best explains snapshost
of the Universe, for example, such as those
taken at the Epoch of Recombination when we view
the Cosmic Microwave Background (CMB).
Viable Topological Tests for the Shape of the Universe
In principle, if we sat down and drew large triangles and measured their
interior angles, we could determine the shape of the Universe. As a
practical matter this is difficult. The other geometric properties of the
Universe are also difficult to measure (as well). Are there other tests we
can apply? Yes.
 |
Angles, Areas, & Volumes
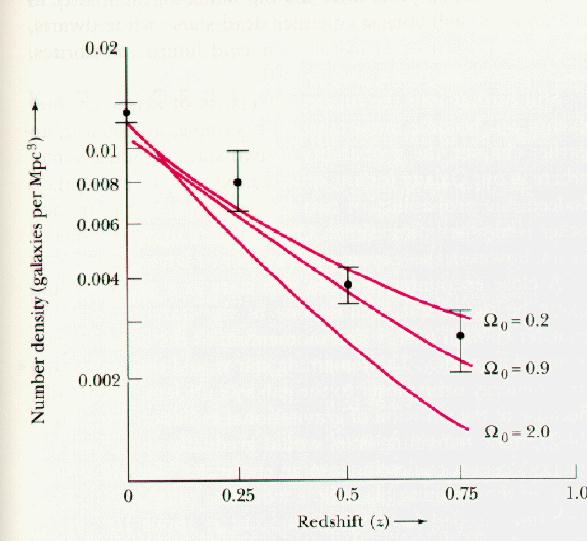
Depending upon the geometry of the Universe, the number density of galaxies
at large redshift (→ large distance) should
depend upon the geometry of the Universe. Why? Well, just as the
area of a circle depends upon the geometry of the Universe, the volumes of
objects may also depend upon the geometry of the Universe. The difference in
the way volumes depend upon distance will affect the way densities depend
upon distance. Tests for this effect have been carried out. The results
are interesting, but not conclusive.
|
 |
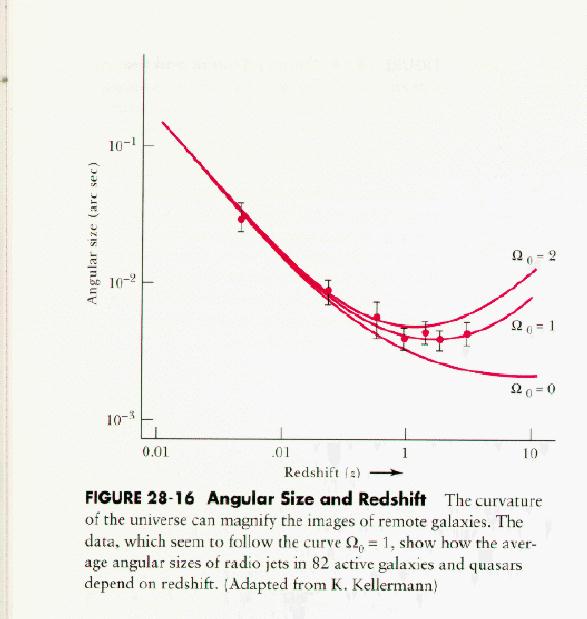
Parallel Lines
Depending upon the geometry of the Universe,
the paths of parallel lines can cross
or diverge, A consequence of this is that if
measures the angular sizes of distant
galaxies, they do necessarily have to decrease as 1/distance (as they
would in a flat universe). This effect has also also been studied. The
results are suggestive but, again, not conclusive.
|
Return to Home Page