The Inflationary Universe

Now and then, I mention perplexing facts about the Universe. I will now go into two of them in more detail and offer an explanation (perhaps).

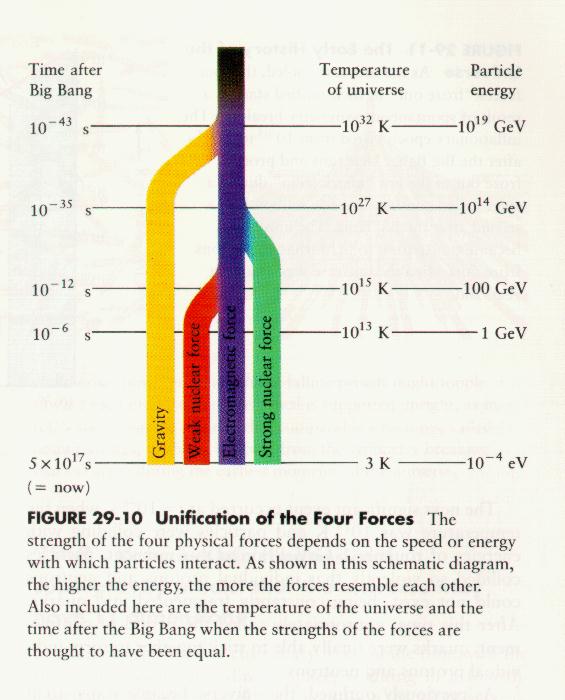
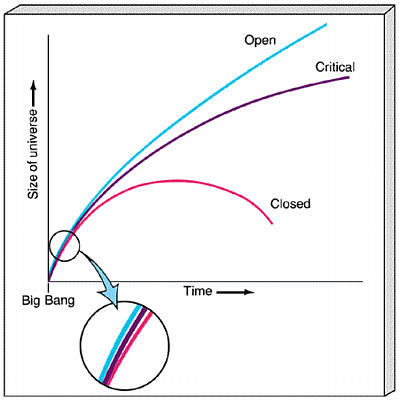
Flatness Problem

The Universe has total Ω ~ 1 or perhaps exactly 1 Is this a problem? Yes.

To understand this point, note that Ω = 1 is special in that the radiation, matter, and dark energy of the Universe conspire to make the Universe precisely flat. If there was a slight imbalance in the begining, we would have problems. To understand this, consider the following.

Analogy: Try and balance a pencil on its pointed end. If you are far from vertical, the pencil falls to the ground very quickly. The closer you can place the pencil to vertical the longer it stands-up before it falls over. If you could place it at precisely vertical then (classically) it could stand-up forever. It is hard to place the pencil at its critcal position.

Universe: If the Universe started off far from critical, then it would have either quickly collapsed (not lasted for 13.7 billion years) or it would have expanded so quickly that it would have passed through the nucleosynthesis and galaxy formation epochs so fast that we would not be here. The only way for the Universe to have lasted this long and to have passed through the nucleosynthesis era at leisurely enough rates requires that the Universe started off very close to critical. How close?

Amazingly,

    Ω must be 1 during the Planck Era to within 60 digits or so

to make Ω(t) ~ 1 today. This is Flatness Problem.

Horizon Problem

The horizon problem arises because light moves with a finite speed. As a result, certain events which occur in the Universe are seemingly completely independent of each other,

The current Universe has a horizon distance of

    horizon ~ age x speed of light → the older is the Universe, the larger is the horizon and therefore the larger is the size of the region which can communicate.

A simple calculation indicates that at the time of recombination, material which was in causal contact (able to communicate) are currently separated by around 0.8 angular degrees on the sky.

This means that the sky could only mix over separations of 0.8 degrees and so, there is no rational reason to believe that the sky should look the same everywhere! This is the Horizon Problem.

The above mysteries may be explained by what is known as the Inflation Theory . Recently results from the Wilkinson Microwave Anisotropy Probe (WMAP) offered strong support for the Inflation theory. To get a handle on inflation recall that the nature of the four forces of nature changes as the Universe evolves:

At earlier and earlier times, the way matter, radiation, and the Universe interact gets simpler and conversely, as the Universe evolves, the way matter, radiation, and the Universe interact get more complicated. Where the forces of the Universe get more complicated are referred to as

    Symmetry Breaking

The end of the GUT era is signaled by the symmetry breaking where the nuclear (strong) and electro-weak forces become distinct forces. This is the event where inflation is driven.

The symmetry breakings are analogous to phase transitions (e.g., liquid water → solid water (ice), liquid water → vapor, etc.). Similar to the phenomenom of supercooling in water, where the phase transition from water to ice is delayed, the phase transition in which the GUT force breaks into the strong nuclear force and the electroweak force can also be delayed. Here, the Universe is trapped in the higher energy state which leads to the repulsive force of inflation. The energy trapped as the Universe lingers in the higher energy phase is abruptly released when the phase transition finally takes place. This effect is nicely demonstrated by supercooled water, freezing water releases heat (Youtube video). The phase transition at the end of the GUT era behaves in this manner.

During inflation, the scale factor of the Universe R(t) evolves as:

Inflation causes the Universe to increase in size greatly and to cool rapidly. At the end of the rapid expansion which occurs after the Universe transits from the false vacuum to the true vacuum, the Universe re-heats and continues on in its normal evolution . Inflation does not affect the long-term evolution of the Universe in this sense; it only produces a rapid blow-up in size of the Universe at an early time.

What are some consequences of this blow-up?

  • For typical models, the Universe roughly doubles in size every ~ 10-34 seconds. This is a phenomenal rate, e.g.,

    • t = 0 sec, the Universe has size 10-24 cm
    • t = 10-34 sec, the Universe has size 2 x 10-24 cm
    • t = 2 x 10-34 sec, the Universe has size 4 x 10-24 cm
    • t = 3 x 10-34 sec, the Universe has size 8 x 10-24 cm
    • t = 4 x 10-34 sec, the Universe has size 16 x 10-24 cm
    • ...
    • t = 100 x 10-34 sec, the Universe has size ~ 13 km

    In the example, the Universe grows by a factor of more than 1030 in 10-32 sec. The exact rate at which the Universe grows depends on the particular model. The point is, expansion is humongous! (Note that in this example, the Universe expands so quickly that even a light beam emitted from a distant observer cannot reach the Earth; the amount of ground it has to cover grows too fast. If the Universe goes from 10-24 cm to 13 km in 10-32 seconds, the average expansion rate is about 13 km divided by 10-32 seconds = 1.3x1033 km per second. The speed of light is 300,000 km per second. The horizon of the observer clearly gets smaller in the sense that we see less of the Universe as time passes during inflation!)

  • Horizon Problem

      Suppose that we start with a large universe and consider a small causally connected chunk say, of size 10-24 cm. Suppose the Universe inflates and that inflation lasts for 10-32 sec, The causally connected chunk of the Universe expands to a size of roughly 13 km. This inflated patch easily encompasses our Universe which, at this time, is only ~ 30 cm in size. Our Universe was embedded in this huge region which was causally connected before inflation,

    This explains the horizon problem.

  • Flatness Problem

      The Earth is known to be spherical, however, for people living on the surface of the Earth, the Earth appears flat. It appears flat because we are not tall enough to see over the edge of the Earth. Due to inflation, we have

      Inflation predicts that the Universe should appear flat (that is, Ω = 1, identically). This resolves the flatness problem.

Eternal Inflation

As the Universe inflates, the false vacuum material starts to decay. The part that decays settles into the true vacuum and normal matter which forms Pocket Universes. The remaining false vacuum continues to grow rapidly (creating more false vacuum --dark energy?); inflation continues indefinitely. This suggests that during inflation, part of the false vacuum keeps growing and inflating while part of the false vacuum decays spawning infinite numbers of Pocket Universes.

Return to Topic 4