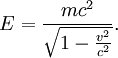The Beginning of Time

ECP Chapter 14 and 17

The Flow of Time
In our Universe, events are specified in spacetime, not simply in space. It is now also well-accepted that the Newtonian notions that space is flat and that there is some universal clock which keeps time for the entire Universe are not true in that time belongs to individual observers determined by their placement in space and by their motion. In spite of this different understanding of the nature of time, we do recognize that, in a certain sense time and space are simply coordinates of the spacetime (however, see next section). Space and time are, however, different in that we cannot (seemingly) jump around in time, revisit points in time. Also, the notion that time flows, each instant exisiting only as it happens, makes sense but is this how time in our Universe is in fact laid out. What are we to make of the notion of time?
The River of Time
As humans, time seems to flow as a river in that the past, the present, and the future are experienecd sequentially and exist in their own times. However, is this or is this not correct? Does time indeed flow in the sense that space is laid out everywhere but time is experienced as a serial string of events, or is it that space and time are both laid out in the way that we imagine space to be laid out everywhere? In the former case, time as flows as we encounter it whereas in the latter, the past, present, and future are already laid out?
In Newton's view, because there is Universal space and time, what we mean by Now is unambiguous. The past is the past, the future is the future, and the present is the present. In Einstein's view (using Special Relativity, what we mean by Now is not as clean; it depends on whether the observer is moving. We can always define what is the past, present, and future for a given obsever, but what events are in the past, the present, and the future depends on how the observer moves. In Einstein's view, no individual (inertial) observer is to be preferred over an another, all are equal in importance. Thus is no preferred past, present, and future in the Universe. All past, present, and future must be laid-out in the spacetime of our Universe. In this sense, time does not flow in the way we currently view the Universe. This is a remarkable (and not common sensical) notion.

SIMULTANEITY
Suppose the train is stationary and a light turns on in the center of the train at time t = 0. The light travels to each end of the train and arrives simultaneously according to observers both in the train and on the ground (in the lab frame). This is illustrated on the plot to the right. The upward slanting lines represent two beams of light which connect the two events; the turning on of the light and the arrival of the light at the front (right hand line) and the back (left hand line) of the train.

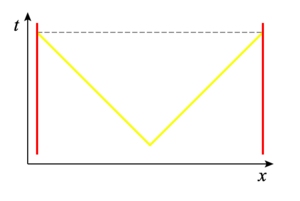Next, suppose the train is moving and a light again turns on at its center at t' = 0. The light again travels to each end of the train and, according to the observer riding in the train, the signal arrives simultaneously at the front and back of the train. This is illustrated in the frame to the left where we show the worldlines for the front and back of the train and the times as measured by a stationary observer. Note that the ends of the train move to larger x as t increases (the lines slant upward to the right). It is clear that the signal arrives at the back of the train before it reaches the front according to the stationary observer (the times as measured on the vertical time axis).

In the panel to the right, we show three cases: a stationary train where the line of simultaneity is horizontal, a frame moving to the right with v < c for which the line of simultaneity slants upward to the right, and finally for a frame moving to the left with v < c for for which the line of simultaneity slants upward to the left.

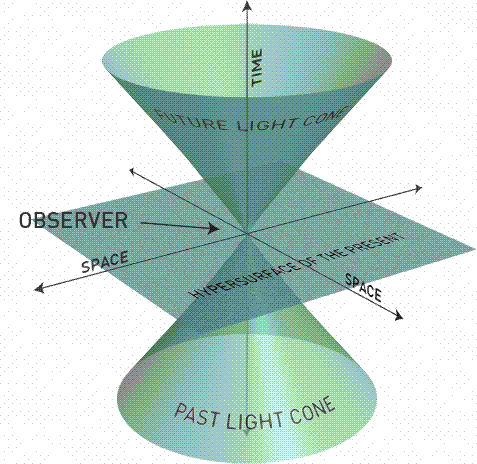The Light Cone, the Future, and the Past
Consider a two-dimensional space + time (see the left panel). If we plot (x,y,ct) so that a trajectory with v = c has slope of 1. In our 2+1 space, this curve sweeps out a cone, the Light Cone. For motion with v < c, the world lines fall inside the cone either pointing upward into the future or backward into the past. If v > c, then the world lines fall outside the light cone.

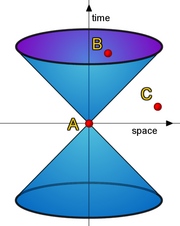Causality
Suppose a signal is emitted at Point A and then received at point B. This trajectory falls within the light cone and so the two events are connected by v < c. For a stationary observer, the event occurs at the marked time and we see that A alwaus occurs before B. Furthermore , for any frame moving with v < c, A precedes B and causality is preserved. (This is known as time-like because a frame exists with v < c where A and B occur at the same location, separated only in time.)
For C, the connection from A to C has speed > c (slope v/c > 1). What happens in this case? Well, for a stationary observer, nothing unusual in that A precedes C and causality is preserved, but the signal does arrive faster than it should. There is also a frame where A and C occur simultaneously at different positions; this is know as spece-like. Furthermore, there is a frame where C will occur before A!!
For a frame which moves sufficiently fast, however, we can get the peculiar result that C may precede A, its cause and we may construct something known as the anti-telephone!! We discuss this possibility in the next section.

For the signal which travels from P to Q, there may be issues for an observer who moves fast enough, even if the observer moves with v < c. The black line marks the curve vt = ct' and the magenta line marks the line of simultaneity (the x'-axis). Note that the signal is sent at time ct = ct' = 0, but is received at time ct' <0 ===> it is received before it is sent.
This odd result can arise if the observer moves with speed
v > 2 a /(1+a²),
where the tachyonic signal travels with speed ac. The possibility of sending a message to the past leads to issues embodied in the what is called the The Tolman Paradox. Benford, Book, and Newcomb (1970) coined one such device an Anti-Telephone ( 1970, Phys. Rev. D, 2 # 2, 263).
Such anti-telephones are theoretically possible, but can people travel backwards in time?

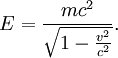Tachyons
In Special Relativity, because we require that the laws of physics are of the same form and that the speed of light is the same for all observers in inertial frames, the energy and momentum of particles must have different forms than which you are familiar. To the left is shown the energy of a particle in free space in Special Relativity. You are more familar with the form

E = 0.5 mv² + mc² Actually we don't usually add the rest mass energy because in classical physics we can't tap this energy and so we just usually redefine the energy as E' = E + mc².

Comments:
If v < c initially, then as v ===> c, 1 - (v/c)² ===> 0 and the energy blows-up; E ===> infinity. This says that if we wish to accelerate a particle whose initial v is < c to v = c, we would need to invest an infinite amount of energy! For tardyons (normal matter), the upper limit to their speed is then the speed of light.
If v > c iniitally, we don't run into this problem and we can have particles with super-light (superluminal) speed. We refer to these particles as Tachyons.
If v > c then 1 - (v/c)² < 0 and we have issues. To make the energy real (as it must be because it is something which we can measure) then this implies that the rest mass of the tachyon must be imaginary. This is okay, however, as tachyons can never be stopped and their rest masses cannot be measured.
Why can't tachyons be stopped? Well, for tachyons, v > c so that if a tachyon slows down, 1 - (v/c)² ===> 0 and the energy blows-up that is the energy of a tachyon become infinite as it slows to v = c. For tachyons, the speed of light is a lower limit to its speed.
If tachyons are charged, then because they have speeds > c, they will emit something known as Cerenkov radiation (see figure in the top panel). As they radiate, they lose energy and so speed up which causes them to radiate more energy which causes them to speed up. This instability drives tachyons to zero energy.

If tachyons exist, then signals can be carried backward in time. But note that we cannot travel back in time as our speeds are always restricted to v < c and we can never become superluminal.

The Arrow of Time
Even if we cannot decide whether time flows or if it is laid out in its entirety, we can describe a sense of the appropriate ordering of events in time, that is, we can define the direction in which time appears to move. We define what is known as The Arrow of Time.

Entropy and the Arrow of Time
Physics is time-reversible. Although not strictly showing time-reversal, Newton's Cradle (see left) illustrates the idea. The causal sense of direction is powerful, but time reversibility suggests there could be issues.
We define something known as Entropy in our Universe (a measure of the disorder in the Universe). The Second Law of Thermodynamics states that entropy stays the same or increases in our Universe (see right). How does the Second Law of Thermodynamics jive with the fact that physics is time reversible?
The increase of entropy is embodied as the Second Law of Thermodynamics offers a natural way to define the flow of time. A cute video of this is the Youtube video posted by Sean Carroll.

Beginning of Time
Shortly after the birth of the Universe, cosmologists are able to follow the evolution of the Universe using physical theory. Later times are on firmer footing than early times; the Planck Era awaits development of a theory which accounts for both quantum mechanics and general relativity. Interestingly, there are attempts to consider these early times. We now describe a couple of ideas.
Hartle-Hawking Theory and the Beginning of Time
Consider imaginary time, what does this mean?

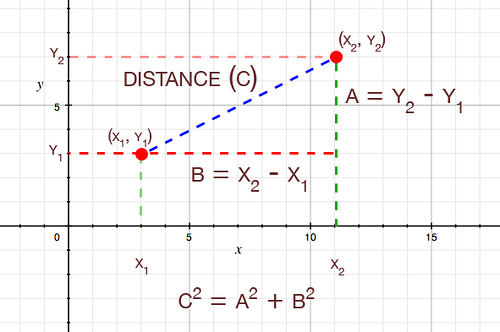
In Euclidean geometry, the distance between two points is given by ds² = (x₂-x₁)²+ (y₂-y₁)²+ (z₂-z₁)²
In Einstein's view of the Universe, we consider space-time and the distance between two events in the Universe in flat space (Minkowski space) is given as
ds² = (x₂-x₁)²+ (y₂-y₁)²+ (z₂-z₁)²- c²(t₂-t₁)² Note that if we consider one location in space then the distance ds² < 0 ===> the separation is the square root of a negative number, an imaginary number! In our Universe, this is a manifestation of the fact that although space and time are viewed simply as coordinates of space-time events, they are treated differently. We have already encountered this notion (in earlier lectures).
If, on the other hand, time intervals are imaginary, then this distinction between spatial and temporal properities goes away and the distinction between space and time disappears. In a universe with imaginary time, things will behave differently and our notion of time breaks down.

A situation as described above may arise around the time of the Planck Era. In the Planck Era, the theories of Quantum Mechanics and General Realtivity must be unified. In such theories known as Quantum Gravity, we find that spacetime behaves quantum mechanically and behaves in a manner consistent with the Heisenberg Uncertatiny Principle. Space and time may fluctuate and we can lose our sense of the meaning of real time in that the ordering of time can become jumbled so that time is more like space and time can be described as equals and time then described as imaginary. In the Hartle-Hawking Theory, it is posited that the Universe moves from a 4-spatial dimension Universe to our 3-spatial dimension Universe (and calculated using something known as Feynman Path Integrals). An upshot of the theory is that the Universe is spatially closed (hmmm). In any event, what is removed is the necessity for initial boundary conditions for our Universe, but it is does offer an idea for the origin of the system.
Hawking suggests that such a situation occured in the early Universe. In this sense, time does not exist (in our accepted sense) before the Big Bang removing the necessity of postulating the beginning of time. Note, however, this notion does not solve the question of where the Universe comes from?, it gives us a way to describe the start of time in our Universe but not what things were like before the Big Bang.