What is Time?

There are many more questions concerning the nature of time than for which I have answers. Questions from a philosophical standpoint concern our perception of time, the reality of time, and even the concept of time. Even from a purely physics standpoint, there are many vexing issues. Does time flow and if it flows, does it flow in a smooth, uniform manner? Is there an Arrow of Time? What would a Universe without time mean? Does time exist independently of the Universe? As corollaries to of these issues, Is time travel possible? And so on and so on. Here, we consider how time has been viewed by physicists and mathematicians over the years.

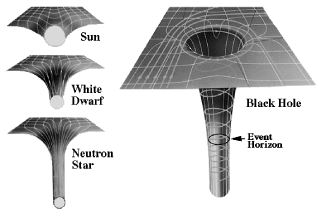
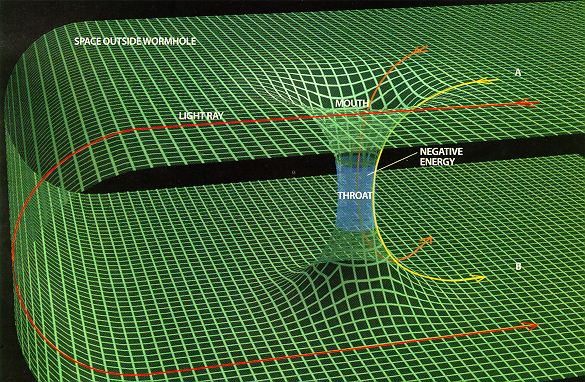
Space and Time
Let us set the stage for a moment. How do we describe the location of events which occur in the Universe? Is it sufficient to give simply the where of the event? No, in order to define uniquely the event, we must also say when the event takes place. That is, if we want to define events in our Universe we must give the location and time of the event. In this sense, time acts as just another coordinate in the Universe much as we define the x,y,z positions for objects in space. This, however, immediately points out that time, although apparently just another coordinate for Universal events, seems to have special properties--we return to the specialness of time later. Space and time form a structure, spacetime, on which (in which) events in the Universe take place. But his also begs the question of whether space and time are things or mathematical constructs.

Issac Newton and the Clockwork Universe
In Philosophiae Naturalis Principia Mathematica (1687), Newton gave his three laws of motion which laid out a prescription for how motions marched forward in time, to the future, in our Universe, given conditions of today. Newton after due consideration, decided space was the rigid framework within which events took place, and considered time as a smoothly (and uniformly) flowing quantity which was the same for all observers in the Universe. Time was simply kept by a Universal clock which inexorably marched forward uniformly and at the same rate for all observers. The Newtonian theory and these notions for space and time work nicely for normal daily events (such as placing astronauts on the Moon) and are perfectly valid for most commonplace situations. (They do breakdown under certain conditions, high speeds, small scales, and/or low energies which we address later.)

Albert Einstein and Spacetime Einstein relaxed the conditions of fixed space and time; he considered non-rigid space and stretchy-squishy time in his famous theories of relativity (the theories of Special Relativity and General Relativity). A notion contained in his General Theory was that of the nature of gravity. Newton postulated a Universal Law of Gravitation, but did not understand how gravity worked. Einstein postulated that effects of gravity arose because of the non-rigid nature of space. Mass distorts the structure of space. In a two-dimensional space, situations such as shown below may arise.

Binary Star Evolution and Gravity Waves
A nice test of some of the ideas of Einstein's General Relativity is the prediction and detection of gravitational waves. The canonical example of this is the binary pulsar, PSR 1913+16 for which Jospeh Taylor and Russell Hulse received the Nobel Prize in physics in 1993. A video animation of another close binary, the white dwarf/white dwarf binary RX 0806.3+1527 (Period=321 seconds!) shows binary star evolution with gravity waves.
Quantum Time
After Newton developed his work in the 1600s, physics developed rapidly and by the end of the 1800s, some audacious folks were suggesting that maybe physics would soon be dead in that nothing would be left to learn. This was before Einstein and Relativity. Further, a second great revolution in physics also occurred in early parts of the twentieth century. Quantum mechanics was discovered which governed physics on small scales and at low energies. We will much more to say about these developments later. One tenet of quantum mechanics is that energy is quantized (it comes in chunks), does this also mean space and time come in chunks as well? To the right we show another facet of quantum mechanics as laid out in the Heisenberg Uncertainty Principle. A consquence of the Heisenberg Uncertainty Principle is that we cannot know an object's location in space and its momentum with infinite precision simultaneously. If we cannot know where something is and its momentum at the present time, then we cannot predict where it will be in the next instant of time. In this sense, we can then also not predict where the particle was in the last instant of time and we now start to question the meaning of the flow of time.