 |
|
 |
|
|

|
 |
|
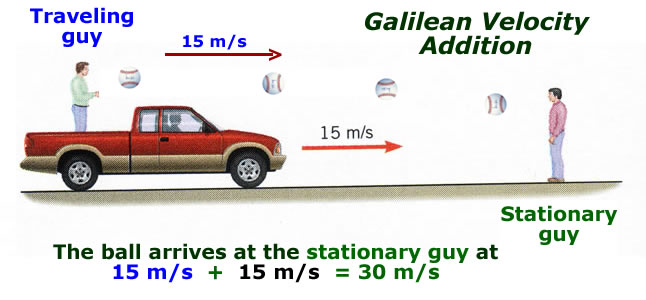
Newtonian Velocity Addition
Vstationary = vtruck + vthrow
In the panel shown to the left, we consider the notion of
velocity addition. There are two observers, one on the truck which moves
with speed
15 m/s and another observer standing on the ground. The truck guy throws a ball
to stationary guy (ground guy). The ball leaves truck guy's hand with a speed of
15 m/s. Sensibly enough, ground guy
catches a ball traveling toward him with a speed
of 15 m/s + 15 m/s = 30 m/s. This is our common
sense simple addition of velocities
rule. This is true in Newton's world where space is
rigid and time flows smoothly
and at the same rate for both observers.
This all seems sensible (it agrees with our notions of
common sense). However, toward the mid to late 1800s, issues were
bubbling up which weren't consistent with this notion of Newton. The most
important of which was the theoretical suggestion that perhaps light traveled
at the same speed in all frames of reference even if the frames of
reference were moving (such as the truck) (James Clerk Maxwell and his
theory of Electromagnetism). This set the stage for Einstein.
Einstein made several bold assertions, a consequence of which was
that Newton's simple velocity addition rule breaks
down for objects traveling at
high speeds, speeds close to the speed of light,
c = 186,000 miles per second or
670,000,000 miles per hour! Things are okay
when we move at speeds slower than this. Cars move at 70 mph and even space
probes travel at only 25,000-40,000 mph. These speeds are much smaller than
c and so Einstein's bold predictions don't strongly affect our
eeryday acitivites.
A consequence of Einstein's assertions is illustrated
in the panel to the right. You sit on a stationary platform and shine a
flashlight to the right. The beam travels away from you with speed c.
Einstein sitting in a bullet
train passes by you which travels with speed v nearly the speed of
c (pretty zippy).
Mr. Newton would say that because Einstein is
in a train moving at the same speed as
the beam of light, that Einstein would see the beam
of light traveling with speed
In Mr. Einstein's Universe, the remarkable prediction is that Einstein would see
the beam of light traveling away from him at the speed of light c. Whoa,
what happened to the law of velocity addition?
Einsteinian Velocity Addition
In Newton's Universe
things behave as your common sense
tells you they must. To As an example of how things change in Einstein's
world view, consider the following simple exercise.


Einstein made two assertions. One is straightforward enough, but the second on
reflection is odd and leads to many strange and wonderful conclusions. Einstein
asserted that:

The first assertion is sensible enough as we are already familiar with such things.
For example,
if you are riding in an airplane which travels at a speed of 500 mph,
you notice that if you drop your pen it falls straight
down (with respect to you).
It also falls down at the rate predicted by gravity.
This occurs despite the fact
you are in the moving airplane. In your little world (your reference frame), all
things behave as if you stationary in your home sitting on your couch
on the Earth. (Uhhh, but are you
really stationary in your home on the Earth;
there are tweaks that should be made
to some of my comments.)
The second assertion (in a sense, simply
helps to guarantee that assertion one is
correct), however, on its face it seems much more remarkable and
leads to some bizarre consequences
which we now explore.
Oh, before we get too far afield, let me point
out that Einstein's postulates given
above are simply assertions. The way
science works is then that the implications of
these assertions are figured out
(that is, the consequences which follow if the above are
true are predicted). These predictions
(in many cases bizarre predictions) are then
experimentally tested. So far in no instance has
Special Relativity been shown to be
incorrect. I point this out
before we go further as many of the things I will
get into will be outside the realm of your common sense and
thus seem fantastical.
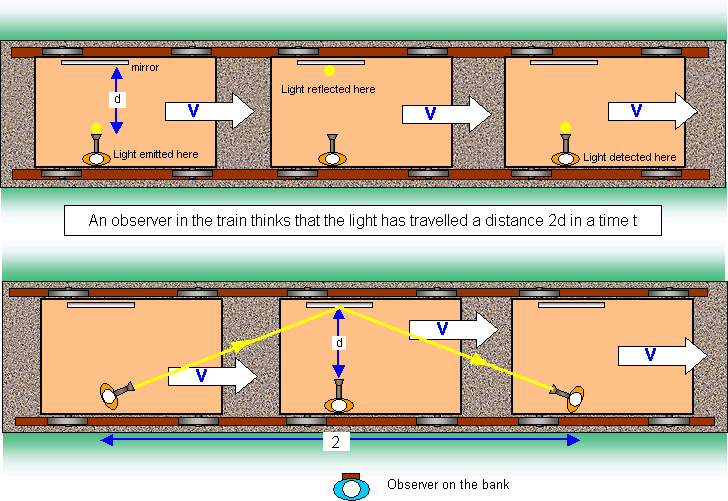 |
The strange idea that the speed of a beam of light measured by different observers will always be c requires some gyrations on our part. What this result leads to is that time must flow differently for different observers. This strange result is time dilation. Let's try to explain how this works. |
An observer on the ground watches the train go by and sees the same events; the beam traveling to the far wall, reflecting off the wall and returning to the observer. Because the train is moving, the stationary observer sees the beam of light follow a longer path 2 x D on its round-trip. Because the observer on the ground also sees the beam of light travel at c, he measures a length of time for the trip of Stationary Guy Time = 2 x D/c > Train Guy. Because we are talking about the same trip, this must mean that Train Guy's watch ran more slowly than did stationary guy's watch since less time elapsed on the trip. Moving guy's clock ran more slowly than did Stationary guy's clock. Let's compare the two times. We have
After a slight manipulation,
Note that 2 x d /c is the time as measured by the moving observer so that
Here, we let T' denote the time as measured by the moving observer. Note that if the train moves at the speed of light, then no time elapses according to the clock of the moving observer, T' must be 0! This effect is known as Time Dilation.
The remarkable thing is that all that is required is for there to be relative motion between the observers so that from moving guy's perspective, staionary guy's clock would run more slowly than his own because staionary guy appears to be moving with respect to him! This notion of relativity leads to the Twin Paradox.
Click on the attached for a nice time dilation video