TIME DILATION AND SIMULTANEITY

We discuss the Twin Paradox, but before we can resolve the paradox, we need to think about what we mean by Simultaneity and Clock Synchronization. Let us first set up the twin paradox.

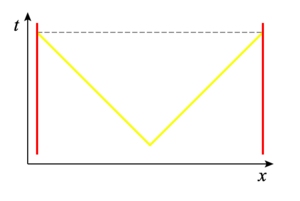
    TWIN PARADOX

    Herb stays on the Earth while his twin Hubert travels to Gliese 581 b 20 light years away in a high speed rocket which travels at 99 % of the speed of light. At Gliese 581 b, Hubert stops, quickly turns-around, and returns to the Earth. Upon their reunion, Hubert finds that Herb is ~40 years older while he has aged only ~5.7 years! The traveling twin has aged significantly less than the stay at home twin. This seems to make sense. So, where is the Paradox? Well, the Paradox artises because of the symmetry of time dilation in that only relative motion is needed for time dilation. So, from the the point of view of Hubert, Herb was the traveling twin, so why shouldn't Herb have aged less?

    SIMULTANEITY

    Suppose the train is stationary and a light goes off in the center of the train at time t = 0. The light travels to each end of the train and arrives simultaneously according to an observer on the ground (in the lab frame). This is illustrated in the frame to the right.

    Suppose the train is moving and a light goes off in its center at t' = 0. The light again travels to each end of the train and again arrives simultaneously according to the observer riding along on the train (the moving frame). This is illustrated in the frame to the left. In the frame to right, we saw three cases: a stationary train where the line of simultaneity is horizontal, a frame moving to the right with v < c for whom the line of simultaneity slants upward to the right, and finally for a frame moving to the left with v < c for the whom the line of simultaneity slants upward to the left.

We see that simultaneity depends upon the observer. If the frame is in motion, simultaneity differs from that for a stationary observer (the horizontal line of simultaneity) and for the moving observer (the slanted lines of simultaneity). Given the notion of simultaneity we can now resolve the TWIN PARADOX.

    Resolution

    The resolution is simple in that the situation is not symmetric. Hubert and Herb are actually different because Hubert must slow down, stop, and speed up, that is, Hubert must accelerate which breaks the symmetry. We can now tell the difference between Herb's and Hubert's motions. Initially, Herb's and Hubert's clocks are synchronized, but when Hubert reaches Gliese 581 b, he hops to a different frame (synchronized differently--the difference leads to the ultimate age difference he and Herb).