Einstein's General Theory of Relativity and Time Travel
In Einstein's Special Theory of Relativity, he addressed motion in reference
frames which were in relative uniform motion with respect to each other
(frames in which the laws of physics were the same and the speed of
light was the same, inertial frames). However, what happens if the
reference frames are accelerated with respect to each other, that is,
the relative velocity between the frames is changing (as occurred in the
Twin Paradox)? To handle this, Einstein developled his General
Theory of Relativity. In Einstein's GTR, he allows space and time to not
only be distorted as in Special Relativity, but he allows for space and time
to be curved (and not flat, Minkowski space). GTR couples the Laws of
Motion and Gravity (and other forms of energy). |

|
Principle of Equivalence
If an observer sees an object fall to the floor of his
or her laboratory, the observer has a dilemma. The observer does not
know if the laboratory is stationary, e.g., on the surface of something
like the Earth, or if the laboratory is accelerating upward, e.g., it
is carried aloft in a rocket. Einstein stated this in the
Principle of Equivalence.
The fact that the effects of gravity cannot be distinguished from those
found in experiments performed in accelerating rockets in space (far away
from any massive object) suggests that gravity is not a real force.
|
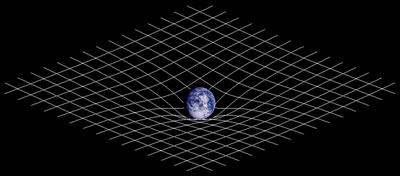 |
Gravity
Einstein sought a geometric
interpretation for gravity.
He noted that objects on flat surfaces which are not subjected to forces
roll in straight lines and that
objects that roll on curved surfaces follow curved paths, even when they
are not subjected to external forces. The natural motion of an
unforced object could either be a straight line (as Newton envisioned)
or a curved line (as would be incomprehensible to Newton) depending
upon the shape of the surface upon which it was rolling.
|
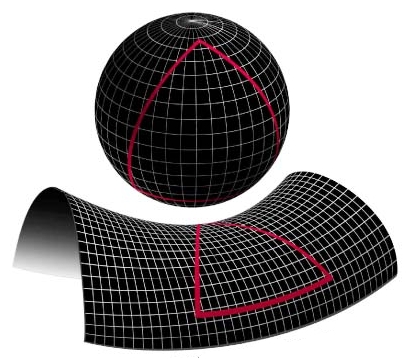 |
Spacetime Curvature
Einstein proposed that
mass and energy distort the shape of space-time
so that falling objects are simply
rolling into depressions and orbiting bodies are simply rolling
>round in the depression. The objects are not undergoing forced
motion; they simply follow the lay of the land. This leads to
the bending of starlight, orbital motion, and, possibly, to extreme
distortions of spactime where we can find Closed Spacelike Paths and/or
Closed Timelike Paths.
|
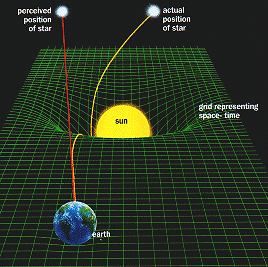
Tests of General Relativity
Einstein became a public celebrity when Arthur Eddington and colleagues
measured the deflection of light by the Sun during the solar eclipse of
1919 and found that their results agreed with the predictions of
general relativity.

Positive print of a Solar Eclipse showing the bending of light |

The Einstein Cross, another example of the bending of light by a gravitational
lens
|
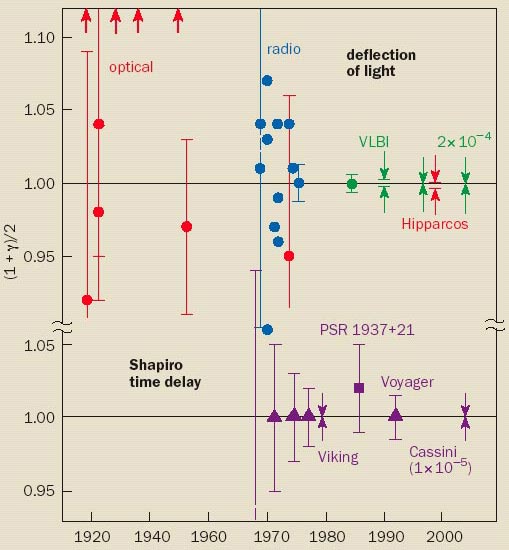
Data for the Solar eclipse measurements and for the time delay (Shapiro
Effect) in a strong gravitational field
|
Deflection of Starlight
Measurements of the deflection
(top) - plotted as (1 + γ)/2, where γ is related to the
amount of spatial curvature generated by mass - have become more
accurate since 1919 and have converged on the prediction of general
relativity: (1 + γ)/2 = 1. The same is true for measurements
of the Shapiro time delay (bottom). "Optical" denotes measurements
made during solar eclipses (shown in red), with the arrows pointing
to values well off the chart; "radio" denotes interferometric measurements
of radio-wave deflection (blue); while Hipparcos was an optical-astrometry
satellite. The left-most data point is the measurement made by Eddington
in 1919, while the arrow just above it refers to the value obtained by
his compatriot Andrew Crommelin. The best deflection measurements (green)
are accurate to 2 parts in 104
and were obtained with Very Long Baseline
Radio Interferometry (VLBI; see Shapiro et al. in further reading).
A recent measurement of the Shapiro time delay by the Cassini spacecraft,
which was on its way to Saturn, was accurate to 1 part in 105
(see Bertotti et al. in further reading).
|

|
Perihelion Advance of Mercury
Mercury is in a highly elliptical orbit about the Sun. Because of perturbations
from the motions of the other planets, Mercury undergoes a slow precession,
574 arc seconds per century, as
it orbits the Sun. Most of the precession (531 arcseconds per century)
is understandable through Newtonian
mehanics, there, however is a small part of the precession
(43 arc seconds per century) which cannot be
accounted for using Newtonian physics.
Using General Relativity, Einstein calculated the small extra
bit of precession, 43 arc seconds per century! |
 |
Gravity Waves
Just as electromagnetic radiation is produced when a charge accelerates,
gravity waves are produced when a mass accelerates
(
Michio Kaku video on gravity waves). As yet, there is no direct detection
of gravity waves, however, there is compelling indirect evidence given by
the binary pulsar, PSR 1913+16. |
 |
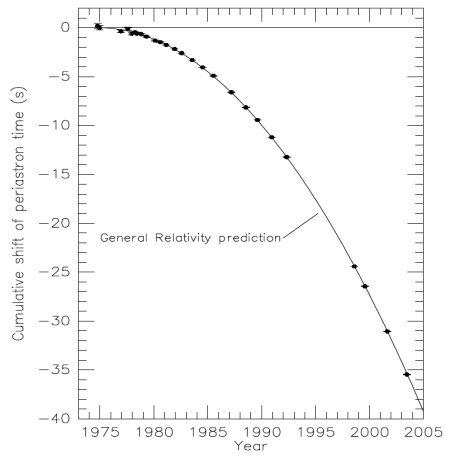 |
Binary Pulsar: PSR1913+16
A pulsar is a rapidly rotating, strongly magnetic neutron star. They are
unparalleled gravity laboratories because of these properties. The binary
pulsar has
Pspin = 0.059 s
Porb = 27,908 s
Orbital ecc = 0.615
Because of gravitational radiation from its orbit, its orbit has been
shrinking. Its orbital period thus slowly decreases. The decrease is shown
to the left! The agreement with Einstein's General Rleativity is
astounding. Hulse and Taylor received the Nobel Prize in physics in 1993
for this
remarkable work. |
Solutions to Einstein's Equations
In Special Relativity, space is flat (Minkowski Space) and the
axes of all light cones are vertical with opening angles of 45o.
Time can only flow forward or backward. In
General Relativity, space can be curved and the axes of light cones may
assume arbitrary angles with respect to vertical, depending on the the
curvature of the space ===> the flow of time can be backwards or
flow in loops in highly
curved spacetimes. This can have interesting consequences.

In the following sections, we consider indicate roughly how curved
spacetimes may lead to closed timelike loops, and then consider several
examples of spacetimes with extreme curvatures in which closed timelike loops
may arise.
 |
Spacetime Curvature
Imagine simple examples of what can happen if we curve spacetime.
Suppose we have the simple 1+1 diagram (1 spatial coordinate + 1 time
coordinate). What happens when we curve the spacetime? |
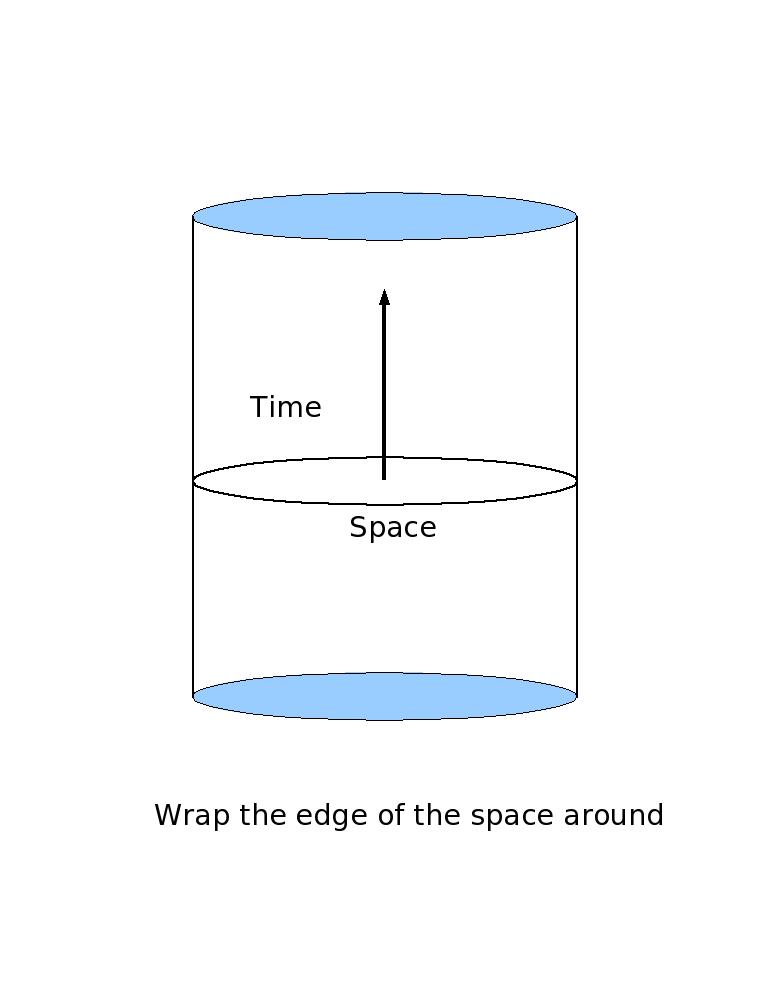 |
Closed Spacelike Loop
Take the left hand edge and the right hand edge of the spacetime diagram and
then wrap them around and glue them together to form a cylinder. We see that
we have formed a closed spacelike loop so that we can simply move around
in space, returning to the same point over and over again even if we
move in one direction. However, in this diagram, if we move one direction in
time, we always move into the future (or into the past).
|

|
Closed Timelike Loop
Perform the same exercise as before but now grab onto the top and bottom of
the spacetime diagram and wrap the edges around and then glue them together.
We see that even when you travel in one direction in time, you can return to
the same point in time many times. In this instance if you move in 1 direction
in space, you never return to the same point.
|
So, we see that there may be the possibility for closed timelike loops
in General Relativity if one can think of a way to curve spacetime.
As a result, there is the possibility for time travel in General Relativity.
An example of this was in the solution found by Kurt Goedel in the 1940s.
 |
Goedel Metric
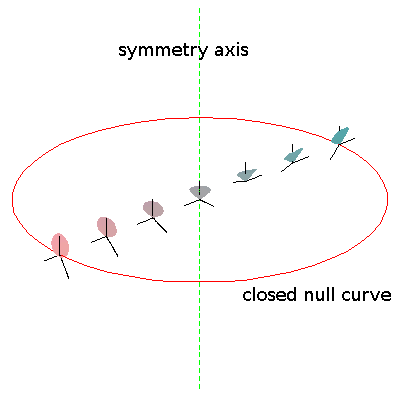
Kurt Goedel (a colleague of Einstein at the IAS) found a solution of
Einstein's equations for a rotating universe which was not expanding or
contracting (therefore not our Universe). In Goedel's universe closed
timelike loops are possible. To see this, look at the panel to the left. As
one moves away from the center, because the universe spins at the same rate,
objects move faster and faster. This acceleration tilts the light cones over.
If one moves far away from the center and moves
at speeds close to but below the speed of light, the light cones are tipped
over nearly on their sides and point along the direction of motion;
one can follow a closed
timelike path and return to the same point in space before one has
left. |
 |