Lecture 4 – Radius ratios and Pauling's Rules
As we have
discussed, the outward symmetry of crystals is an expression of internal
ordering of atoms and ions in the crystal structure. This in turn reflects the intrinsic symmetry of the packing
of atoms, and their interaction with neighboring atoms...
The
ultimate reason for a particular arrangement of atoms in a mineral structure
lies in the nature of the cohesive forces that hold atoms together. In theory, we should be able to predict
a mineral structure from the chemical composition, but in reality the problem
rapidly becomes too complex to solve.
We'll be
discussing the subject of crystal chemistry for the next few weeks - defined as
the elucidation of the relationship between chemical composition, internal
structure and physical properties of crystalline material.
A
reminder: the chemical composition
of the Earth's crust - 8 elements make up ~99 wt% of the crust ("major
elements") ... O and Si are most abundant, thus most common minerals are silicates and oxides.
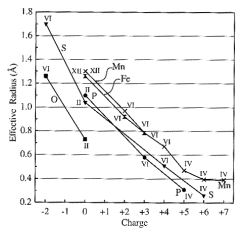
Ionic
radii
Size
of atoms difficult to define, let alone measure. Determined be maximum charge density, which itself is a
function of the type and number of nearest neighbor atoms. Therefore it is possible to assign each
ion a radius
such that the sum of the radii of two adjacent ions is each to the interatomic
(separation) distance. Thus we can
determine effective radii by measuring bond lengths in crystals.

Within
a given period (say, the alkalis), the radius increases with atomic number.
(Table 13.1)
Radii
also vary systematically across a row, being smaller at the center (cation
charge increases) and largest to the right (the anions; Table 13.2).
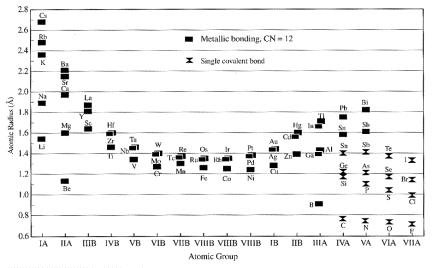
Ionic
radii depend strongly upon the valence state of the ion, with larger sizes for
negative ions and smaller sizes for positive ions (Table 13.3, 13.4).
EX:
S+6: radius
= 0.6 A
S: radius
= 1.04 A
S-2 radius
= 1.7A
Finally, the size of an ion is dependent on its coordination
number.
Coordination
number
Many
simple mineral structures can be viewed as close packing of large anions, with
smaller cations in interstitial sites. The anions are packed in a regular
structure, while the cations fit in between. The number of anions to which a particular cation bonds is
the cation’s coordination number. EX: Si+4
typically bonds to 4 O atoms, and therefore has a coordination number of 4.
The size of
the interstices depends how the anions are packed – different in 2- and
3-dimensions.
EXAMPLES
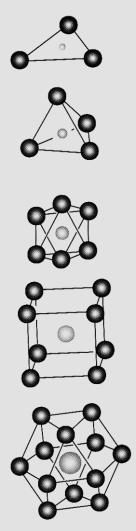 We give coordination arrangements
geometrical names:
We give coordination arrangements
geometrical names:
2-fold linear
3-fold triangular
4-fold tetrahedral
6-fold octahedral
8-fold cubic
12-fold dodecahedral
Closest packing
What is the
most economical way to pack spheres?
2D: If spheres of equal size are packed together as close as
possible in a plane, they arrange themselves as follows:
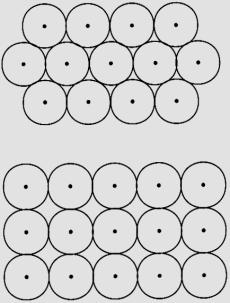
Center of
spheres are at the corners of equilateral triangles; each sphere is in contact
with 6 others. Note that within
this layer there are 3 close-packed directions, each at 60o.
Unit cell is hexagonal, with lattice parameter a = 2r. Packing is 90.7% efficient. Hexagonal (closest) packing
Here the
center of spheres are at the corner of squares, each sphere is in contact with
4 others. There are only two
close-packed directions and the unit cell is square. Packing is 78.5% efficient. Tetragonal packing
Closest
packing in three dimensions
Metals have structures that are
typically formed by close-packing of atoms, around which electrons pass
freely. This type of structure is
highly ordered so as to minimize void space.
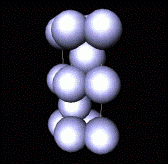 Build 3-D structure by placing these
layers one on top of the other.
Most economical way of doing this is such that spheres in one layer rest
in hollows of layer below. Two
different positions are possible, B or C.
(choice equivalent to rotating 180o). By doing so, create a layered sequence
of AB.
Build 3-D structure by placing these
layers one on top of the other.
Most economical way of doing this is such that spheres in one layer rest
in hollows of layer below. Two
different positions are possible, B or C.
(choice equivalent to rotating 180o). By doing so, create a layered sequence
of AB.
Let's add a
third layer. Again, we have two
choices. If third layer goes above
A position: ABABABABA
simplest
form of close packing - hexagonal closest packing (has underlying hexagonal lattice)
… this is true for Na metal
If third
layer goes in the C position, stacking sequence would be ABCABCABC.
cubic
closest packing
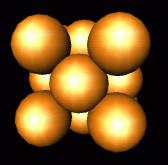 (has underlying cubic lattice). In
both of these closest packing sequences, each atom has twelve equidistant
nearest neighbors, six in its own plane, and three each in the layer above and
the layer below. Examples include
Au (shown to the left), Ag, and Cu.
(has underlying cubic lattice). In
both of these closest packing sequences, each atom has twelve equidistant
nearest neighbors, six in its own plane, and three each in the layer above and
the layer below. Examples include
Au (shown to the left), Ag, and Cu.
This simple structure means that metal atoms of similar size
can easily substitute for each other, thus allowing for alloys of metals like
silver and gold. Because of the
close packing, metals are dense; they are also malleable and good electrical
conductors.
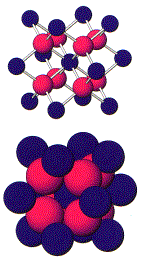
Other minerals that have a cubic closest packed structure
are
sphalerite halite
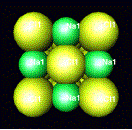

ZnS NaCl

 Most minerals are not formed by
metallic bonds, and thus do not have this simple structure. For example, the covalent bonds of
diamond are strongly directional, which prevents the atoms from adopting a
close-packed structure. As a
consequence, diamond has a lower specific gravity than a typical metal.
Most minerals are not formed by
metallic bonds, and thus do not have this simple structure. For example, the covalent bonds of
diamond are strongly directional, which prevents the atoms from adopting a
close-packed structure. As a
consequence, diamond has a lower specific gravity than a typical metal.
Ionic
Bonding
One
of the most successful models for predicting crystal structure is to treat
crystals as packing of anions and cations as different sized spheres… these
rules are collectively known as Paulings Rule and can be summarized as follows:
1. The Coordination (radius ratio)
Principle – a
coordination polyhedron of anions surrounds each cation. The cation-anion distance is determined
by the sum of the cation and anion radii and the number of anions coordinating
with the cation is determined by the relative size of the cation and anion.
2.
Electrostatic Valency Principle – in a stable ionic structure, the total strength of the
valency bonds that reach an anion from all neighboring cations is equal to the
charge of the anion.
3.
Sharing of Polyhedral Elements I – the existence of edges (and particularly faces) common to
coordination polyhedra decreases the stability of ionic structures
4.
Sharing of Polyhedral Elements II – in a crystal containing different cations, those with
large valence and small coordination number tend not to share polyhedral
elements with each other.
5.
Principle of Parsimony – the number of essentially different kinds of constituents in a crystal
tends to be small.
We’ll look
at each rule separately.
Coordination
(radius ratio) Principle:
This principle states that the number of anions with which a
cation coordinates is determined by the ratio of their radii rc/ra.
Bottom
line: most stable configuration is
achieved when oppositely charged ions (e.g. Na+ and Cl-) are as close together
as possible without overlapping.
Inter-ionic distance determined by the balance of electrostatic
attractive forces between outer electron charges, and repulsive forces between
nuclei. Thus in 3 dimensions, ions with positions that
follow principles of ionic bonding form highly symmetric polyhedra (coordination
polyhedra) that
have same inter-ionic distances - will
control where certain cations fit into crystal structures. Tetrahedra and octahedra are most
common structural types, but triangles, cubes, and other forms important. These coordination polyhedra link
together in various ways to form the polyhedral-frame structures. Include all of rock-forming silicates,
as well as many borates, sulfates, phosphates, tungstates, oxides, hydroxides.
To
reiterate, a coordination polyhedron of anions is formed about each cation, the
cation-anion distance being determined by the radius sum and the coordination
number of the cation by radius ratio.
Thus when bonding dominantly ionic, each cation in the structure will
tend to attract, or coordinate, as many anions as will fit around it.
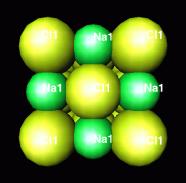
NaCl
Appropriate
radii:
 Na+ = 0.097nm
Na+ = 0.097nm
Cl-
=
0.181nm (almost twice as large)
rc/ra
= 0.54
If we
imagine these as rigid spheres, how closely can we pack them?
First let’s
look at 2 dimensions. If the
radius of the cation is very small relative to the cation, the cation can fit
into small space between three close-packed anions. As the cation becomes larger, the anions move farther apart. At some ratio of ionic radii, closest
packing switches to one in which the cation is surrounded by 4 anions (this is the case for NaCl)
From
trigonometry:
![]()
 rc
/ ra = .414
rc
/ ra = .414
Thus the
radius ratio between anions and cations tells us how the spheres can be
packed. For smaller ratios, all 4
anions would not touch the cations, and distances would not be minimized. For larger ratio, distance between
anions > 2ra, and eventually a new configuration becomes stable.
What about the third dimension? In order to maintain rc/ra = .414
(minimum separation = closest packing), we must add two additional anions, one
above and one below. Thus each
cation is in 6-fold (octahedral) coordination.
In
general:
|
Rc/Ra |
Expected coordination of cation |
C.N. |
|
<0.15 |
2-fold coordination |
2 |
|
0.15 0.15-0.22 |
ideal triangular triangular |
3 |
|
0.22 0.22-0.41 |
ideal tetrahedral tetrahedral |
4 |
|
0.41 0.41-0.73 |
ideal octahedral octahedral |
6 |
|
0.73 0.73-1.0 |
ideal cubic cubic |
8 |
|
1.0 > 1.0 |
ideal dodecahedral dodecahedral |
12 |
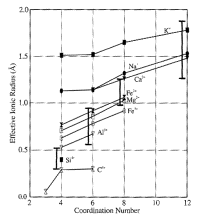
Let’s return to our model of close-packed spheres. As you determined in lab, stacking of
close-packed layers of spheres generates two kinds of interstices:
tertrahedral
site between 4
close-packed atoms. Thus any small
atom occupying this site will be tetrahedrally-coordinated with its
neighbors. Tetrahedral sites form
in two distinct orientations - apex pointing up or apex pointing down. For this reason, there are twice as
many tetrahedral sites as there are close-packed ions (one above and one
below).
octahedral
site is larger -
has 3 atoms below and 3 above.

NOTE: when
one close-packed layer is placed on top of another, both types of sites are
created. Specifically, there
are two 4-fold sites and one 6-fold site per sphere.
Let's look
at elements in rock-forming minerals.
O ranion = 0.13 nm
Radius
ratios with oxygen:
Si4+ = 0.30nm
Al3+ = 0.47nm
Si fits
into range for tetrahedral coordination - usually found tetrahedrally
coordinated in silicate minerals.
However, Al in boundary region between tetrahedral and octahedral
coordination... In natural
minerals it is found in either coordination.
Most other
common cations in Earth's crust fall in range of octahedral coordination.
Electrostatic
valency principle:
we can calculate the strength of a bond (its electrostatic valence) by dividing
valence by coordination number (CN). As a consequence, in a stable crystal structure the
total strength of the valency bonds that reach an anion from all neighboring
cations is equal to the charge of the anion. The rule is a direct consequence of ionic bonding... total
bonding capacity of a cation is proportional to its charge (z): z/CN
Ex.
rutile TiO2
Ti+4 is in octahedral
coordination with oxygen. Each
Ti-O bond has a strength Z/CN = 4/6 = 2/3. Each oxygen has three neighboring Ti+4 cations such that their collective bond strength (3 x 2/3)
equals the oxygen charge of -2.
For this reason, anions tend to be locally charge-balanced.
SOME
CONSEQUENCES:
A. Geometrical
and electrical stability - (Ex. fluorite, CaF2). Each Ca has 8 fluorine neighbors, while each
fluorine has only four Ca neighbors.
rCa = .99A rF
= 1.33A rc/ra = .74
Even though
relative sizes would allow closest packing, charge balance requires the 2:1
ratio, and thus determines the structure.

Fluorite
and halite illustrate another consequence of rule 2, which is that when all
ionic bonds have the same strength, anions pack together in a highly symmetrical arrangement,
thus these minerals are highly symmetric. Minerals with uniform bond strengths
include the oxides, fluorides, chlorides, etc.
In
contrast, when there are nonuniform bond strengths, crystal structures have lower
symmetry. This is true when
structures include small cations of high charge (C4+, S6+,
P5+, Si4+).
Additionally, this rule means that the number and kinds of coordination
polyhedra that can meet together at a point are severely limited. For example, no more than 2 Si4+
tetrahedra can share a common oxygen, even though the radius ratio
considerations alone would permit three, four or more ... each Si-O bond
contributes an electrostatic strength of 4/4 = 1, so that two Si-O bonds will
just satisfy the -2 charge of the oxygen.
Similarly, exactly three divalent cation octahedra will share a common
oxygen with a Si4+ tetrahedron. Mineral groups included in this category are the carbonates,
sulfates, phosphates
and silicates.
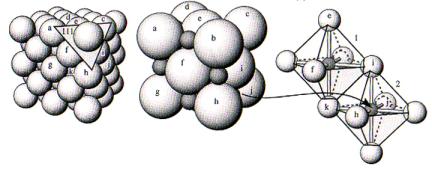
3) Sharing of polyhedral elements. I. The existence of edges, and particularly of faces, common to
two anion polyhedra in a coordinated structure decreases its stability. Direct outgrowth of electrostatic
forces... Most stable
configuration is when two polyhedra share only a corner, because then the two
central cations are as far apart as possible.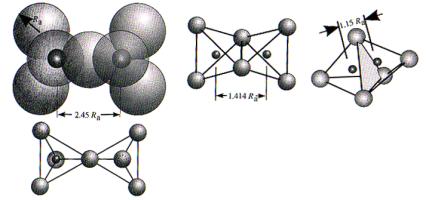
The figure
above shows that the more anions shared between polyhedra, the closer the
positively charged cations. This
reduces stability, particularly when the cations are highly charged (e.g., Si4+).
4) Sharing of polyhedral elements
II. In a crystal containing different
cations, those of high valency and small coordination number tend not to share
polyhedral elements with each other.
Corollary of rule three - emphasizes the fact that highly charged
cations will be as far apart from each other as possible. Effect stronger if coordination number
is low. Ex. - no silicate minerals
have edge-sharing or face-sharing Si tetrahedra. However, edge-shared octahedra are common (TiO2,
or, as shown in the diagram below, NaCl), and even face-shared octahedra are
found (Fe2O3).
5) The principle of parsimony. Number of essentially different kinds of constituents in a
crystal tends to be small because, there are only a few types of cation and
anion sites. No more than two or
three different types of coordination polyhedra in a mineral. The number of crystallographically
different sites is thus small - fundamental reason why various cations and
anions in chemical fromulas are generally in small integer ratios to each
other. Relative abundance
controlled by availability of sites in a structure. Thus in structures of complex compositions, a number of
different ions may occupy the same structural position (site).
Summary:
It is
possible to regard a crystal as being made up of AXn groups that are joined
together by sharing corners, edges or faces of coordination polyhedra rather
than as individual ions... we'll see a lot more of these. Coordination polyhedra commonly
distorted.
1.
polyhedral framework structures
Most
of rock-forming minerals in this category, especially silicates. All structures are direct consequence
of predominantly ionic bonds between constituent ions. As result of bonding, anions tend to
group around cations in highly symmetric manner to define coordination
polyhedra.
Ex: silica tetrahedron (SiO4)-4
divalent
cation octahedra (MgO6)-10
By sharing
apical oxygens, polyhedra link together to define a structural frame that
possesses at least half of the total bonding energy of the mineral - resulting
frame is relatively strong and has important influence on most physical and
chemical properties.
2.
Symmetrically packed structures
Either
bonds between atoms are nondirectional or bond directions are highly symmetrical.
Ex. metallic bond, also many examples of
covalent and ionic.
Atoms form
highly symmetrical structures in which atoms packed together in symmetrical
ways:
a)
monatomic (native metals) - if atoms are in contact in and between sheets -
highly efficient packing called closest packing. If atoms lose contact within sheets but retain contact
between sheets - close-packed.
b)
mulitatomic - both cations and anions... many oxides, sulfides, halides and
most of important silicates considered as framework are in this category. Anions are in symmetrically packed
sites, and cation soccupy voids between.
symmetry of anion packing is basic
characteristic.
3.
Molecular structures
Composed
of atoms characterized by strongly directional and low symmetry bonds. Asymmetric bonds form strong clusters, chains
and layers of atoms that behave as discrete units connnected by much weaker
bonds to for 3-D networks. Ex: ice