Quiz on Electricity, Magnetism and Waves Overview: The Science of Spectra Introduction to Heat and TemperatureThe Science of SpectraWaves-- repeating patterns that travel across water, air, solids and even empty space-- are found in many forms in the physical world. The beauty of the notion of waves is that, once we have observed how waves travel and interact on a pond, we can use the same model to understand how light waves bend and reflect to give an iridescent sheen to a mud puddle. The parameters describing waves along with the mathematical relationships between them describe many, many wave-like phenomena in our everyday world.
Let's look at water waves in a baking dish to observe some wave phenomena.
Now let's look at a filmstrip that better shows these interesting phenomena.
Electromagnetic waves comprise the radiation we receive from the sun, and from each other. X-rays, visible light, microwave and radio waves are all examples of EM radiation.
These waves are characterized by:
Period (T)
the time {seconds} between crests of the wave)
Frequency (f)
the inverse of period-- 1/T {in 1/seconds}. How fast a wave is bouncing up and down. ("color" of wave).
Wavelength (l)
the distance {meters} between crests of the wave at a given time
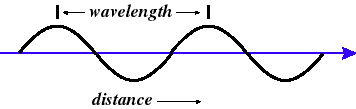
Wave Speed (v)
the distance the crest of one wave moves in a second {meters/second}. The speed of most everyday EM waves is close to the speed of light, "c," approx. 300,000,000 m/s.
EM waves comprise electric and magnetic fields that change over time and position, similar to the waves on a lake. If one puts a charge in the path of an EM wave, and gives it a medium on which to travel, it will bob up and down (or side to side, etc.). Electric forces cause it to move.
{note: the electron on the antenna does not necessarily "follow" the sine wave representing the electric field. The latter shows the force on the electron and, consequently, its acceleration. Its position along the antenna would be derived from its initial position and acceleration over time.}
Now let's look at a video that better shows how EM radiation works.
Light waves exhibit the same sort of phenomena as do water waves. For example, the many different colors (frequencies) of white light will bend differently upon entering a prism.
Light waves will also bend upon passing through a "diffraction grating." Lets look through one and observe the light from a Neon gas lamp and from the overhead lights.
Interesting! Are all colors of light present in the EM radiation from the overhead lights?
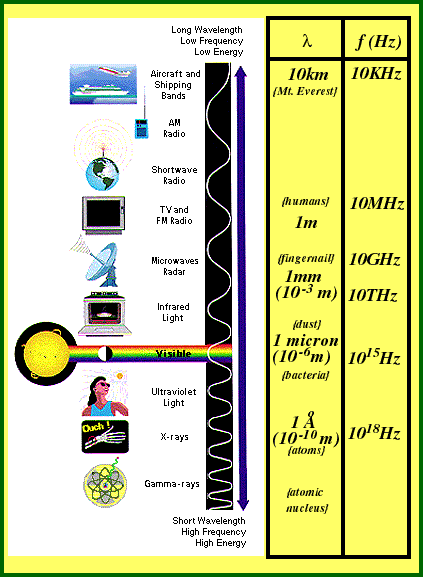
In traveling through empty space, all EM waves travel at the same speed. We call this "the speed of light" ("c"), which is approximately 300,000,000 meters / second. What differentiates one type of EM wave from another is the frequency and wavelength of the particular wave. This also determines what we call that particular type of radiation.
Most emitters of electromagnetic waves broadcast radiation over a range of frequencies. We call the "spectrum" of the emitter. For example, we can see a range of frequencies just below 1015 cycles/second {Hertz}. We call this the "visible spectrum."
Note: Remember that, because all EM radiation travels at the speed of light, a "range of frequencies" is the equivalent to a "range of wavelengths."
{adopted from Imagine! the Universe Home Page}
Spectrum, isn't that something my dentist uses?
Have you every wondered why doctors have "X-rays" taken to image bone in the body? The wavelengths for different types of EM radiation vary enormously. Besides having the ability to pass through skin and other soft tissue in the body, X-rays also have a very small wavelength! This means that they are affected by the very small distances between atoms in bones when they pass through them. We call this "resolution."
Simply put, visible light rays, IR radiation, microwaves and radio waves have too long a wavelength to "resolve" bone matter from soft tissue.
A similar process allows you to listen to your radio while traveling under a bridge. Radio wavelengths are on the order of meters, which is also the size of most bridges. Hence, radio waves don't "resolve" (aren't affected by) the bridge.
We can devise a simple tool that allows us to examine the spectrum (range of frequencies) of a light bulb at a certain temperature, T1. With this tool we could measure the intensity (brightness) of each color of light (visible and invisible) emitted from the bulb.
Physicists call something that emits and absorbs radiation in an ideal way a "blackbody." Any EM radiation emitted or absorbed by a blackbody will depend only on its temperature.
If we undertake the same experiment for a similar blackbody emitter, but one with a greater temperature, we see that the wavelength of the highest intensity decreases (which is the same as saying that the frequency increases). Also, and importantly, the bandwidth-- the span of covered wavelengths-- increases.
Using my "spectral analyzer" (above), I could plot the spectrum of the Sun. Assuming that the Sun is a blackbody, I could then estimate its temperature. Experiments show that the total radiated power (P) over all wavelengths for a blackbody is related to its temperature by:
P = s A T4 {Watts}
where s is a universal constant (5.67 x 10-8 W/m2 K4), A is the area of the radiating surface (of the Sun in this case) and T is the temperature in Kelvin.
Why is this important?
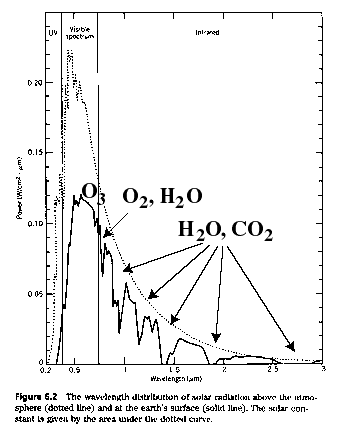
Well, the sun emits radiation (mostly infrared+light+ultraviolet) as if it were a black body at 5900 degrees K. Compared to the approximately 300 degree (K) Earth, it emits over a broader bandwidth and with a higher peak frequency.
(source: Energy & Problems of a Tech. Society- Kraushaar & Ristenen, absorption lines adopted from Piexoto & Oort, Physics of Climate)
The Earth is so cool as to not emit visible light. It radiates over a spectrum that is much narrower and shifted to longer wavelengths (lower frequencies). CO2 and other "greenhouse gases" absorb certain of the lower frequencies and heat up. They re-radiate this heat into the Earth's atmosphere and reflect some of it back towards the Earth. Because of this phenomenon, the Earth is inhabitable, without it the Earth would be quite cold! Of course, too much CO2 can be thought of as too much of a good thing.....
A well-designed solar collector will absorb this higher-frequency radiation but stay relatively "cool" in the process. It, too, emits radiation as a black body, but it emits much of it at infrared ("heat") and lower frequencies. The glass on top of the collector will reflect this radiation, effectively trapping the thermal energy inside.
Introduction to Heat and TemperatureAfter a cold day out skiing, we head inside to sit next to a fire and "heat up." But what exactly do we mean by this? Also, when we burn gasoline to provide energy for our car, or we drop water through a turbine at a hydroelectric power plant, we inevitably lose energy to "heat." Again, what do we mean by heat?
When we listen to the weather forecast, a key piece of information is the prediction of what temperature it will be tomorrow. We know that a warm temperature, say 60 degrees Farenheit (ok, ok, it's winter here now) means that we can wear a lighter coat. If it is expected to be cold, we wear a heavier coat, i.e. one that insulates us better from the cold. An object's temperature is related to the "hotness" of the body.
Thermometers tell us what the temperature of an object is. This reading tells us, evidently, something about heat. Temperature is typically measured in degrees Celsius, where a temperature of 0 C is where water freezes and 100 C is where water boils (when the US catches up with the entire rest of the world, we will come to understand temperatures in degrees Celsius, not degrees Farenheit, where water freezes at 32 F and boils at 212 F).
What happens when a hot object, one with a high temperature is placed in a colder environment? Say, for example, that a red hot piece of metal is dropped in room temperature water. Over time the metal will cool and the water will heat up. Eventually the two objects will have the same temperature. They are then said to be in thermal equilibrium with one another.
During the intervening time the hot metal is doing work on the water. How can we tell? The water might boil, for example. A piston could be placed over the water in a sealed container, and the piston would lift, much like the lid rattling on a pot of boiling water. The piston would gain gravitation potential energy in lifting, so work had to be done on it. The work came from the hot piece of metal.
So energy is transferred from the hot metal, eventually, to the piston. Evidently heat involves some sort of energy transfer. And a temperature difference is necessary for that energy transfer to take place. That is, unless we could lift the piston somehow by putting a piece of room temperature metal into room temperature water (NOT likely).
To get a better understanding of temperature and heat energy, consider a box full of gas atoms or molecules at some temperature, T. If we built our box with transparent sides and could somehow see the molecules or atoms inside, what would they be doing? What if we marked just one molecule so that we could see it, and restrained its motion to two dimensions?
Here are some questions to ask yourself when watching this movie:
Previous Lecture 
Next Lecture 
Back to Course Page. 
