Reading: Chapter 24, pages 550-562.

Reminder-- Homework (assigned Tuesday, 2-November): Chapter 8, problems 2, 3, 6, 7, 9, 27, 36, 38. Due Thursday, November 11.

Heat and Temperature

• Heat is energy

• An aside: absolute zero

• Adiabatic compression

• First Law of Thermodynamics

• Other ways to change internal energy

• An example, the hydrological cycle

• Mechanisms for heat transfer-- conduction, convection and radiation

• An example, energy conservation in the home.

What happens when a piece of hot metal is dropped in room temperature water. Over time the metal will cool and the water will heat up. Eventually the two objects will have the same temperature. They are then said to be in thermal equilibrium with one another.

During the intervening time the hot metal is transfering energy to the water. How can we tell?

The water can do more work than it could before. The water might boil, for example. A piston could be placed over the water in a sealed container, and the piston would lift, much like the lid rattling on a pot of boiling water. The piston would gain gravitation potential energy in lifting, so the heated water did work on it. The original energy came from the hot piece of metal.

So energy is transferred from the hot metal, eventually, to the piston. Evidently "heat" involves an energy transfer. And a temperature difference is necessary for that energy transfer to take place.

Consider a simple model comprising hot gas molecules in a cool box.If we built our box with transparent sides and could somehow see the molecules inside, what would they be doing? What if we marked just one molecule so that we could see it, and restrained its motion to two dimensions?

Here are some questions to ask yourself when watching this movie:

• What happens to the particle's velocity (v) in the x (horizontal) direction when it collides with a wall of the box? Does its direction change? (duh!) Does its magnitude change?
• What must the box exert on the particle in order to change its velocity (direction)?
• If the box exerts a force on the particle, does the particle exert a force on the box wall?
• If we define pressure as force per area, do we have a basis for describing the pressure the gas (particle) exerts on the walls of the box?
• If the particle speeds up on the average, what happens to the pressure?
• If the particles is more massive (but with the same average speed), what happens to pressure?
• If the particle speeds up on the average, what happens to temperature?
• What is the relationship between pressure and temperature at constant volume?

An aside on absolute zero

You will remember that the temperatures given above for black bodies were listed in "Kelvins." What is a Kelvin? Why do we use it?

It turns out that there is a temperature--absolute zero-- where particles in a system have no kinetic energy (they don't move). The temperature of such a system is 0 Kelvins. So Kelvins are units of temperature which reference absolute zero.

We can estimate absolute zero with a simple demonstration, predicated on the proportional relationship between temperature and pressure for an ideal gas at constant volume.

Adiabatic Compression

We spoke of transfering heat energy to water from a piece of hot metal. Typically the water, in turn, loses its newly-gained thermal energy to its surroundings. The whole process takes time.

What if we do work on a gas and don't give it time to lose heat energy to its surroundings. What happens to the gas?

Interactive Lecture Demonstration, Part B:

We can simulate what happens to the gas molecules during adiabatic (no heat transfer) compression by using the following QuickTime movie:

When we do work on the system (W), we increase its internal energy (DU, following the notation in our textbook), as evinced by an increase in temperature. We can state this finding as a simple equation:

DU = W

This says that doing work on a system changes its internal energy by an amount equal to the work. (what happens if work is done by the system?)

We can do a demo that shows this increase in internal energy very dramatically:

Suppose I took a syringe full of air but with a little bit of paper at the bottom. Suppose I rapidly pushed down on the plunger? What would happen? How is this process represented by the first law of thermodynamics? What can we say about the internal energy of the air in the syringe? What can we say about heat energy transfer?

First Law of Thermodynamics

Now what if I very slowly pushed down on the plunger? Would the paper ignite? Why or why not?

Pushing down slowly gives the system (gas in the tube) time to cool down, via heat energy transfer to its surroundings. So, evidently, transfering heat energy (-DQ) to its surroundings decreases internal energy.

{If we define DQ to be heat transfered to the system, then -DQ is heat energy transferred from the system.} We can summarize this as follows:

This is just a statement of energy conservation in disguise. In fact, this is the most general statement of energy conservation one can make. The (internal) energy of a closed system changes by transferring heat energy in (DQ is positive) or out of it and by doing work on it (W is positive) or having it do work on its surroundings.

IMPORTANT NOTE: A system refers to group of objects and the boundary around them. The internal energy, DU, is a measure of the state of a system. It, like temperature and pressure, are state variables. They all tell you about the "guts" of a system. Heat energy transfer, DQ, and work, W, are done either on or by systems. They involve energy transfer between a system and its surroundings, across the system boundary. One does not speak of the "work of a system" or the "heat energy of a system."

Other ways to change internal energy

So how do we tell what the internal energy of a system is? It seems we should take its temperature, but there are other ways to change internal energy without changing temperature.

We can see how heat energy can be transferred into a system without changing its temperature by considering our low-tech demonstration. A pan of water has been sitting on a burner since the beginning of lecture. We noticed that, at first, the water's temperature increased while it was heated by the burner. After the water began to boil, the temperature remained constant. The change in internal energy of the water thereafter takes the form of liquid water turning into vapor

Sunlight absorbed by ocean water can raise the water's temperature. Or it can cause the liquid water to turn into water vapor, even though the water is NOT boiling. This is how energy from the sun drives the hydrological cycle:

In the Pacific Northwest and elsewhere humankind exploits the hydrological cycle-- a mechanism whereby fresh water is transported to and from oceans; into and out of lakes, streams and glaciers; and back and forth from underground reservoirs-- to provide electrical energy from a hydroelectric plant.
We also rely on the hydrological cycle to: Transfer energy from the sun falling on the oceans to continents. Distribute more equally water resources across land masses. Increase erosion of rocks and soils covering the continents. Regulate atmospheric temperature (see point 1).	Thanks, Greg!
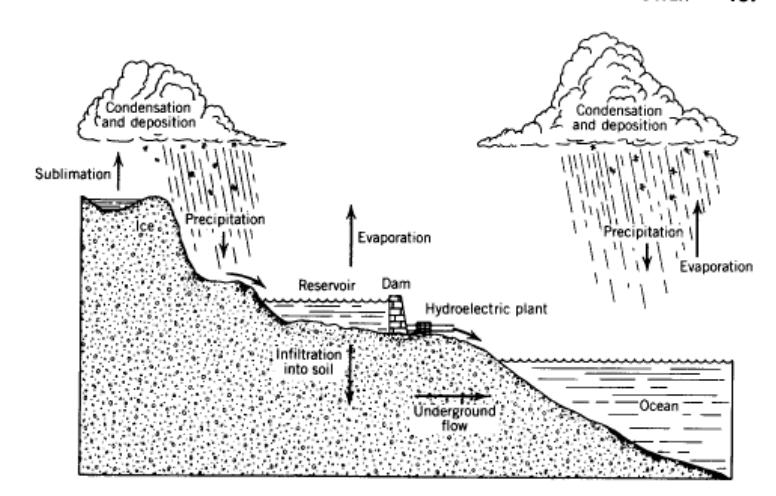
The latent heat of evaporation describes the amount of heat energy transfer necessary to turn a given amount of liquid water into vapor form. This energy ultimately derives from the sun. The conversion of the sun's energy to evaporate ocean water is one of the primary mechanisms driving the hydrological cycle. So hydroelectricity is just another form of "solar energy!"

Mechanisms for Heat Energy Transfer

Heat energy can be transfered by three different mechanisms:

• Convection: This involves the material moving, literally carrying the heat energy away. For example, you may have noticed that, on a hot day a road surface can appear to be shimmering. This is because heat energy is being transferred away from the road by air rising above it. The "shimmering road" illusion is caused by random motions of this convecting air affecting the light that shines through it.
• Conduction: Conduction requires a solid material and a temperature difference across it. Have you ever tried to drink steaming hot coffee or cocoa from a tin cup? Then you know about conduction of heat energy.
• Radiation: Unlike convection and conduction, radiation of heat energy from a hot body to a cooler one can take place without any material in between. Also, the object that is giving up heat energy need not be touching the object being heated. Radiation of heat energy is how you warm yourself by standing next to a cozy woodstove. The heat energy is transfered via electromagnetic (EM) waves.

Radiation of heat energy from the sun is responsible for life on Earth.

An example-- Energy conservation in the home

To better understand the three mechanisms for heat energy transfer, imagine you were charged with doing things to lower the heating bill (weatherize) an ancient cathedral in Bath, England.

1. The first thing you should do is repair all those fancy windows and doors. They are a source for drafts (not the game played in pubs), where warm air leaks to the outside and is replaced by cold air from outside. This is heat energy by convection, because warm air is moving, taking heat energy with it. Studies show that cutting down air leakage is the most cost-effective form of weatherization.
2. The next thing to consider is insulating the ceilings, walls and floors of the cathedral. Insulation cuts down on heat energy transfer out of the building via conduction. As warm air typically accumulates near the ceiling (why is that?), a greater difference in temperature exists between the ceiling and outdoors than elsewhere in the building. That is the place to start adding insulation.
3. After you have caulked (cut drafts) and insulated ye ole cathedral, its time to think of extreme measures. For example, you might want to paint the outside of the cathedral black so that it better absorbs heat energy from the sun. Why is this extreme? Well, it really is the least cost-effective thing you can do. Heat loss or gain by radiation is usually a small factor affecting a building heat budget. Besides, whether this helps or not really depends on the temperature outdoors. During summer you may end up overheating the cathedral. And then where would they sing evensong?

To get a perspective on how the energy used to heat buildings compares to other forms of energy use in the US, let's look at table 24.3 from your textbook:

Use	Percent of US Fuel Consumption	Second-Law Efficiency (%)
Space heat	18	6
Process steam	17	25
Auto transport	13	10
Truck transport	5	10
Water heat	4	3
Air conditioning	2.5	5
Refrigeration	2	4

Source: Energy by Aubrecht, page 556.

Evidently space heating represents a substantial part of the US energy budget!

All that aside, conservation of a building's thermal energy can be thought of as another energy source. Because a weatherized building uses less energy for heating, that saved energy can be used elsewhere. Conservation of thermal and other forms of energy has an added benefit. Compared to the second-law efficiencies of various energy conversion processes (we'll get to that next lecture), energy conservation is 100% efficient!

For more information about heat transfer mechanisms and weatherizing a home, see Prof. Bothun's page on insulation in the home.

We can do a simple calculation to estimate the yearly energy savings when insulating a house. Insulating a house involves cutting heat energy loss by conduction. The rate at which heat flows through a system boundary (Q) is given by:

Q = k A DT / t {J/s}

where k is the thermal conductivity, A is the area of the boundary (say the wall of a house), DT is the temperature difference across the boundary, and t is time.

We can restate this rule in more common units of thermal resistance, R, as:

R Q = A DT {ft^{2 o}F}

The "R-value" of insulation is typically written on home insulating materials and, in the US, assumes units of square feet and temperature differences in degrees Farenheidt. Its US units are {hr ft^{2 o}F / BTU} (note the hour).

For a home with a given R-value for walls, ceilings and floor, and a fixed area for heat energy transfer, a greater difference in temperature (DT) results in a greater heat flow rate. The average daily difference between the temperature outdoors and an assumed indoors temperature of 65 ^oF is called a degree-day.

Degree-days are compiled for various locations around the US and abroad. For example, the degree-days for Eugene are approximately 4,200.

If the Eugene heating season is 150 days long, what is the average daily outdoor temperature?

So degree-days are a convenient way of stating both temperature difference and time. To calculate heat loss by conduction using degree-days, we write:

Q = degree-days x 24 hr/day x A/R {BTUs}

(The hour/day conversion converts degree-days to degree-hours, so as to cancel with the hours in the units of R.)

Previous Lecture Next Lecture Back to Course Page.