according to (Philibert, 1968) :
John J. Donovan*, Donald A. Snyder** and Mark L. Rivers***
* Department of Geology and Geophysics, University of California, Berkeley, CA, 94720
** Department of Geological Sciences, University of Michigan, Ann Arbor, MI, 48109
*** Argonne National Laboratory, University of Chicago, Chicago, IL, 60637
REFERENCE
J. J. Donovan, D. A. Snyder and M. L. Rivers, "An Improved Interference Correction for Trace Element Analysis" Microbeam Analysis, 2: 23-28, 1993
INTRODUCTION
Spectral interferences (also called peak overlaps) occur whenever the wavelength of the characteristic x-ray used for analysis is near to or coincides with the characteristic x-ray line of one or more matrix elements and can be a serious source of error in quantitative microanalysis. For energy-dispersive spectrometry, the relatively poor resolution of Si(Li) detectors can induce large spectral interferences and consequently considerable effort has been expended in addressing this problem (e.g., Fiori et al., 1981 and Myklebust et al. 1981). On the other hand, little attention has been paid to interferences in wavelength-dispersive spectrometry, possibly because of the inherently higher resolution of the technique. Nevertheless, there are many analytical situations in which an inaccurate interference correction can create large analytical errors, even for wavelength-dispersive spectrometry analysis. In this paper we present an improved algorithm for the quantitative treatment of interference corrections in wavelength-dispersive spectrometry x-ray microanalysis. We then show cases of trace element analysis where errors due to spectral interferences occur and demonstrate through analyses of standards that even in these worst cases, the correction recommended in this study successfully accounts for the spectral interference(s).
The technique that we develop is an empirical one in which the interfering counts are estimated at the desired peak intensity wavelength and does not involve estimation of the entire background due to interferences. Such spectral processing techniques have been proposed and have been calibrated for specific instruments (e.g., Roeder, 1985). Although these techniques can provide adequate corrections, they are in general time-consuming to calibrate and are sensitive to details of machine configuration. We present an easily implemented, flexible correction scheme that is not sensitive to various machine configurations.
EMPIRICAL ESTIMATION OF SPECTRAL INTERFERENCES
A quantitative interference correction requires an accurate estimate of the intensity of the interfering element. This intensity can be calculated from the ZAF corrected concentration of the interfering element in the unknown, the measured interference in a standard used for the interference correction, and the ZAF correction factors for the matrices of both the unknown and the interference standard.
In general , the concentration of
an element A can be determined from its characteristic x-ray
emission at wavelength according to (Philibert, 1968) :
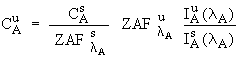(1)
where the following notation has
been adopted : 
is the concentration of element i in matrix j; 
is the ZAF
(atomic number, absorption and fluorescence) correction term for
matrix j (Z and A are for wavelength 
and F is for the
characteristic line at 
for element i); and 
is the measured
x-ray intensity excited by element i in matrix j at wavelength .
In the case in which element A is
interfered by another element B (Fig. 1), the measured x-ray
counts at 
are the sum of those excited from elements A and B so that
(2)
where 
are the total
measured counts at 
and 
are
the uninterfered counts from element A. To estimate 
, we can write,
motivated by equation (1) :
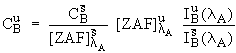(3)
where 
refers to an
interference standard which contains a known quantity of the
interfering element B, but none of the interfered element A. Now
re-arranging (3),
. (4)
Since 
is determined
independently from
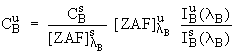, (5)
all of the necessary terms are known and equations (2) and (4) can be combined with equation (1) to yield :
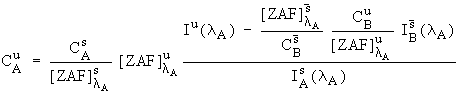. (6)
It is difficult to estimate the F terms in equation (4) because knowledge of all the excited lines would be required. Fortunately, except in some unusual cases, these F terms are generally near unity (most of the corrections tend to be in the Z and A components) and can be neglected. Consequently, we have approximated equation (6) with
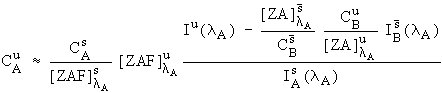, (7)
and it is this expression that we use in our following data reductions.
Similar approaches have been taken previously for WDS (wavelength-dispersive spectrometry) interference corrections, but have adopted far more approximations. For example, a commonly used scheme (e.g., Gilfrich, et al., 1978) is to take
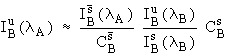. (8)
In contrast to equation (4), this
expression neglects the matrix effects of the unknown, analytical
standard and interference standard (at 
and 
) on the observed
counts excited from element B. Hence any differences in the ZAF
corrections between the unknown and standards will create a
systematic analytical error. Further, if A is a trace constituent
in a matrix containing abundant B, these correction errors are
greatly magnified. In the following sections, we use actual
analyses on well characterized standards to explore the
ramifications of these assumptions and test the validity of our
correction scheme.
ANALYTICAL METHODS
For this study all data were
acquired with an ARL SEMQ eight spectrometer
wavelength-dispersive microprobe at the University of California
at Berkeley. Samples were run at an operating voltage of 15
kilovolts using a sample current of 40 nanoamps as measured on
synthetic MgO. Analyzing crystals were chosen to minimize the
interferences in all cases by selecting the smallest 2d spacing
crystal that could be used for the analytical line. Detector slit
widths were normally 2-4 millimeters. All measurements were
off-peak corrected after careful spectrometer scanning to ensure
that both off-peak positions were free from any interfering
lines. Pulse height analysis was used for all measurements.
Typically the on-peak counting time was 40 seconds, the off-peak
counting time was 20 seconds on each off-peak position and each
result was calculated by averaging some 20-40 points. All
analyses were calculated using the integrated CITZAF 
matrix
correction routines (Armstrong, 1988) within the PRSUPR program
(Donovan, et al., 1990 and 1992).
We tested each algorithm by incorporating both equations (7) and (8) into the ZAF iteration loop of the PRSUPR electron microprobe data acquisition and data reduction program, shown schematically in Fig. 2. Because interference corrections are most important in trace element analyses, we used this routine to analyze several well characterized standard reference materials which contain trace elements that experience severe spectral interferences. After correcting the x-ray count data for deadtime, background, beam and standard drift, both expressions were evaluated and the errors calculated. The results appear in Table I.
In addition to using an accurate correction scheme, errors caused by spectral interferences in WDS analysis can be reduced by instrumental settings. For example, if the interfering line is a higher order reflection, the interference can be reduced or nearly eliminated by careful use of pulse height analysis or by judicious selection of an analyzing crystal which naturally suppresses that high order reflection. Interfering lines of the same energy can only be reduced by the use of higher resolution analyzing crystals (i.e., smaller 2d spacing) and/or narrow detector slits. All of these methods however, can reduce signal intensity and increase the sensitivity of the analysis to intensity, peak shift and peak shape changes (Goldstein, et al., 1981).
RESULTS
We have analyzed five analytical standards to (1) illustrate that the method presented successfully corrects for interferences, even in especially difficult cases and (2) show when simpler methods do and do not fail.
In the first example we
demonstrate the equivalence of the two expressions by measuring
the concentration of Zr in an aluminum-magnesium-phosphorus oxide
glass sample (NIST SRM K-497) using an analytical standard and an
interference standard both (NIST SRM K-496) almost identical in
composition to the sample. Consequently, even though the
uncorrected overlap by the 
line is almost 120%, the ZAF coefficients
nearly cancel and the two expressions yield similar values (Table
I.).
Such ideal standards are,
unfortunately, rarely available. For example, when determining
the concentration of a trace level of Ti in a silicon-barium-zinc
oxide glass sample (NIST SRM K-963) which is significantly
interfered by the 
line, although the analytical standard used (NIST
SRM K-489) to determine Ba is essentially identical to the
sample, the barium fluoride (BaF) standard used for the
interference measurement was not.
At the analytical wavelength for Ti the differences between the ZA(F) correction for the sample (Z * A = 1.046) and the interference standard (Z * A = 0.914) were large enough to affect the calculation of the interfering counts ( 0.914 / 1.046 = 0.873); this causes equation (8) to overcorrect the interfering intensity by some 13%.
A third example is of particular
interest to geologists as determinations of trace F in the
presence of a 
spectral interference are quite common in silicate
minerals such as biotite 
and amphibole 
. Here we
examined an amphibole standard containing a known concentration
of F and 8.90% FeO using a W/Si layered dispersive element (LDE)
analyzer. Although the spectral overlap from with an LDE
analyzer is much greater than that seen with the traditional
crystalline rubidium acid phthalate (RAP) and thallium acid
phthalate (TAP) analyzers, the increased count rate from the LDE
improves the detection limit of the light elements significantly.
However the interference correction also becomes more important
due to the lower resolution of the LDE.
For this measurement we used a
natural magnetite (approximately 
) as the interference standard and a
biotite standard as the analytical standard for Fe. The effect on
the analytical intensity of the 
(and the interfering ) line by these
various matrices is considerable, ranging from 200-350%. In Table
I we can see that the difference between the two values
from each expression is about 500 ppm for this sample. Samples
containing less F and more Fe will produce even more divergent
results.
Several analytical difficulties
arise in situations where large fluorescence effects are present.
The most serious of these are when either the matrix absorption
or the fluorescing x-ray, within a sample, affect the fluoresced
analytical and/or the interfering lines in different ways. For
example, in K band fluorescence, both the 
and the 
are equally
fluoresced by characteristic lines of other matrix elements.
However, if a major element absorption edge lies between the two
fluoresced K lines, they will suffer unequal degrees of
absorption. This would be the case, for example, in Ni - Fe
alloys with significant concentrations of Mn, since the manganese
absorption edge lies between the Fe 
and the Fe 
lines, both of
which are fluoresced by the Ni line.
L line fluorescences are more complicated primarily because situations exist in which not all L lines are fluoresced equally by a characteristic x-ray. This is due to the fact that several absorption edges exist for the L band. Examples can be found where the primary analytical L line is fluoresced by a characteristic x-ray, but the secondary L line of the same element which is causing an interference with another element, is not. In both of the above K and L band fluorescence scenarios, the use of equation (8) will cause errors to be introduced in the interference correction calculation.
But what of K band fluorescences
where no major element absorption edges lie between the
fluoresced analytical line and a secondary line causing an
interference? In such cases the fluorescence effects on the
interfering element cancel. Therefore, because equation (8)
completely neglects the matrix correction of the interfering
line, only the absence of the absorption and atomic number
corrections are of concern, whereas, equation (7) can slightly
underestimate the fluorescence contribution to the interference
correction because of the dropped F term in our approximation of
the matrix correction of the interfering x-ray. In fact, with K
band fluorescences it might be desirable to retain the F terms
for the correction of the interfering line by using the value
calculated for the primary analytical line of the interfering
element and use the full expression of the interference
correction as shown in equation (6). However, we can see from the
Fe - Ni alloy in the fourth example (SRM 1159), that the effect
of the missing F term is small. Here the 
line is
interfered by the line of Fe which is in turn significantly fluoresced
by the presence of Ni in the sample. Even though the matrix
correction for the interfering line in equation (7) only corrects
for the absorption and atomic number effects, the difference
between the two expressions is only about 140 ppm and our model
still yields the better analysis.
In a final example, we have analyzed trace Cr in a titanium-aluminum-vanadium alloy (NIST SRM 654b) where a major concentration of Ti causes an interference on V, which in turn strongly interferes with the Cr analytical line. Because equation (7) is incorporated into the ZAF iteration loop of our quantitative analysis program, the concentrations of each element are correctly determined after several iterations. Equation (8) on the other hand dramatically overcorrects the V interference on Cr resulting in a negative weight percent.
CONCLUSIONS
We have reported a more refined technique for the accounting of spectral interferences in wavelength dispersive spectrometric analyses. Accurate interference corrections are most important for trace element analyses. We have shown that while approximate techniques based on raw x-ray counts can yield adequate results in some circumstances, they will fail for trace element analyses in which there are mutual fluorescences and absorptions between the interfering and interfered elements or when the standards and unknown samples have different matrices. The method presented here overcomes these obstacles and is recommended for general use in the correction of x-ray peak intensities for spectral interferences.
ACKNOWLEDGMENTS
The authors wish to thank John Armstrong and Paul Carpenter at the California Institute of Technology, the late Chuck Fiori of the National Institute of Standards and Technology and two anonymous reviewers for their valuable suggestions and advice.
REFERENCES
Armstrong JT: Quantitative
Analysis of Silicate and Oxide Materials: Comparison of Monte
Carlo, ZAF, and Procedures, In: Microbeam Analysis-1988,
Ed. DE Newbury. San Francisco Press, San Francisco, 1988, pp.
239-246.
Donovan JD, Rivers ML: PRSUPR: A PC-Based Automation and Analysis Software Package for Wavelength-Dispersive Electron-Beam Microanalysis, In: Microbeam Analysis-1990, Eds. JR Michael, P Ingram. San Francisco Press, San Francisco, 1990, pp. 66-68.
Donovan JD, Rivers ML, Armstrong JT: PRSUPR: Automation and Analysis Software for Wavelength Dispersive Electron-Beam Microanalysis on a PC. American Mineralogist 77, 444-445 (1992).
Fiori CE, Swyt CR, Gorlen KE: Application of the Top-Hat Digital Filter to a Nonlinear Spectral Unraveling Procedure in Energy-Dispersive X-Ray Microanalysis, In: Microbeam Analysis- 1981, Ed. RH Geiss. San Francisco Press, San Francisco, 1981, pp. 320-324.
Gilfrich JV, Birks LS, Criss JW: Correction for Line Interferences in Wavelength-Dispersive X-ray Analysis, In: X-Ray Fluorescence Analysis of Environmental Samples, Ed. TG Dzubay. Ann Arbor Science Publ., Ann Arbor, 1978, p. 283.
Goldstein JI, Newbury DE, Echlin P, Joy DC, Fiori C, Lifshin E: Scanning Electron Microscopy and X-Ray Microanalysis. Plenum, New York, 1981.
Myklebust RL, Fiori CE, Heinrich KFJ: Spectral Processing Techniques in a Quantitative energy Dispersive X-Ray Microanalysis Procedure (FRAME C). NBS Special Publication 604, pp.365-379 (1981).
Philibert J, Tixier R. Quantitative Electron Probe Microanalysis, In: NBS Special Publication, Ed. KFJ Heinrich. Washington, D.C., 1968, p. 13.
Roeder P: Electron-Microprobe Analysis of Minerals for Rare Earth Elements: Use of Calculated Peak-Overlap Corrections. Canadian Mineralogist 23, 263-271 (1985).
TABLES
Table I. Comparison of analyzed trace elements in samples using both the traditional count ratio interference correction (equation (8)) and the method presented in this study (equation (7)).
| Matrix | Element | No Correction | Equation (8) | Equation (7) | |
| wt% | wt-% % dev | wt-% % dev | wt-% % dev | ||
| SRM K-497 | Zr 0.32a* | 0.702 +119.% | 0.364 +13.7% | 0.364 +13.7% | |
| SRM K-963 | Ti 0.290b | 0.377 +30.1% | 0.274 -5.52% | 0.292 +0.7% | |
| Amph-357 | F 0.26 | 0.355 +36.4% | 0.225 -13.6% | 0.271 +4.1% | |
| SRM 1159 | Co 0.022 | 0.145 +560% | 0.010 -55.3% | 0.024 +8.9% | |
| SRM 654b | Cr 0.025 | 0.268 +971% | -0.020 -184.2% | 0.021 -16.6% | |
a Value not certified
b Value determined by atomic absorption
SRM K-497 includes : P 31.59, Mg 6.49, Al 5.97, O 52.46, Pb 0.86, Ce 0.94, Ta 0.71, Ti 0.22, Fe 0.26, Si 0.13
SRM K-963 includes : Ba 39.53, Si 22.23, Zn 2.93, Pb 1.32, O 31.70, Al 0.11, Zr 0.40, Ti 0.27, Ce 0.80, Ta 0.95, Fe 0.35
Amph-357 includes : SiO2 39.31, Al2O3 15.37, MgO 13.89, K2O 1.36, TiO2 4.14, Na2O 2.36 O 0.47, CaO 12.54, FeO 8.90, MnO 0.10
SRM 1159 includes : Ni 48.2, Fe 51.0, C 0.007, Mn 0.30, P 0.003, S 0.003, Si 0.32, Cu 0.038, Cr 0.06, Mo 0.01
SRM 654b includes : Ti 88.974, Al 6.34, V 4.31, Fe 0.23, Si 0.045, Ni 0.028, Sn 0.023, Cu 0.004, Mo 0.013, Zr 0.008
FIGURE CAPTIONS
Figure 1. Schematic diagram showing a hypothetical spectral interference.
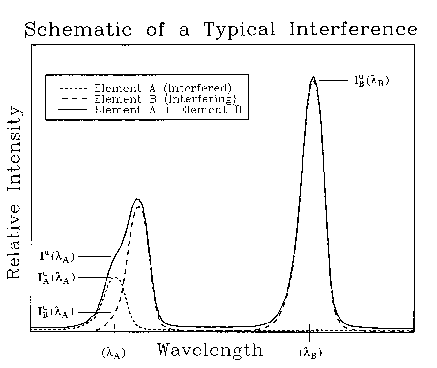
Figure 2. Flow diagram of the interference correction presented in this study.
Back To Department of Earth and Planetary Science Home Page