(1)(this page is best viewed using Netscape 3.01 or higher)
By John J. Donovan
Department of Geology and Geophysics, University of California, Berkeley, CA, 94720-4767
J. J. Donovan (1998) Using Quantitative Iteration to Correct for Pathological Spectral Interferences, in: Proc. Microbeam Analysis Society, San Francisco Press, San Francisco (in press)
A number of problematic analytical situations are known to exist in electron probe microanalysis (EPMA) where characteristic x-ray spectral overlaps are not only severe, but are also of the "self-interfering" or "cascade" variety. The "self-interfering" variety is exemplified by the innocuous Ba La « Ti Ka to the fearsome Pb La « As Ka binaries, while "cascade" interferences are often seen among the transition metal series as in Ti Kb ® V Ka - V Kb ® Cr Ka or as seen with a secondary fluorescence interference effect as in Ni K Þ Fe Ka - Fe Kb ® Co Ka. Unlike simple interferences of the type Mn Kb ® Fe Ka, both of these types of spectral interferences are often quite troublesome for the analyst to correct for, especially for Si(Li) and Ge energy dispersive spectrometers (EDS) where the analytical peaks are often so overlapped as to prevent graphical deconvolution, and even for the higher resolution wavelength dispersive spectrometers (WDS) along with the yet to come bolometric energy dispersive detectors (based on projected resolution), the task can still be formidable. This abstract will focus on WDS methods, since this method represents the best resolution currently available (and the typical ultimate resolution in EPMA for the foreseeable future), to deal with these especially difficult types of spectral interference.
The general method used here to calculate and correct x-ray intensities for spectral overlap based on peak intensities, as opposed to working with complete spectra. One technique that has been used by many analysts (often as a "back-of-the-envelope" calculation), is usually modeled on a simple ratio of the interfering and interfered intensities. The expression seen here (e.g., Gilfrich, et al., 1978), for the determination of the interfering intensity, is commonly utilized,
(1)
where the following notation has been adopted :
is the
concentration of element i in matrix j, 
is the measured
x-ray intensity excited by element i in matrix j at wavelength 
; and where
element A is interfered element, and element B is the interfering
element, u is the unknown matrix, s is the standard matrix and 
refers to an
interference standard which contains a known quantity of the
interfering element, but none of the interfered element. The
quantity 
is
then subtracted from the intensity of the interfered element, to
obtain the actual intensity.
Since the degree of spectral interference is actually not directly dependent on the intensity of the interfering element, but is rather, compositionally dependent on the concentration, a rigorous correction for interference requires two important modifications to the method described above. First, it is necessary to quantitatively correct for the matrix effects on the interfering intensity in both the unknown matrix and the interference standard matrix as seen here,
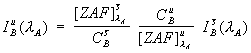(2)
where 
is the ZAF or frz matrix correction factor for element i in matrix j.
Second, the full matrix adjusted interference correction
expression shown above, should then be enclosed inside an
additional iteration loop to allow the interference to be
recalculated after the concentration of each interfered element
is subsequently determined based on the new matrix correction
(see Donovan, et al., 1993).
To evaluate the efficacy of the quantitative iteration method for correction of spectral interference, several analyses of both the "cascade" and the "self-interfering" varieties are discussed briefly and compared using equations (1) and (2).
Looking at Table I, we can see that equation (1) overcorrects both the interference due to the secondary fluorescence of Fe Ka by Ni and the Ti Kb ® V Ka - V Kb ® Cr Ka "cascade" interferences. On the other hand, equation (2) using a quantitative iteration handles the situation easily.
In the case of "self-interfering" interferences, we can see in Table II, that small interferences, such as the Ba La « Ti Ka system, are not difficult to deal with, even using equation (1). However, the situation involving Pb La « As Ka is obviously untenable using expression (1), while equation (2) provides quite usable results in spite of a prolonged iteration procedure of approximately 50 iterations.
Table I, Analyses exhibiting interferences of the "cascade" variety.
wt. % (nominal) |
wt. % (uncorrected) |
wt. % (Eq. 1) |
wt. % (Eq. 2) |
|
| Ni K Þ Fe Ka Fe Kb ® Co Ka |
Co 0.022 1 | 0.089 ± 0.008 | 0.010 | 0.022 ± 0.008 |
| Ti Kb ® V Ka V Kb ® Cr Ka |
Cr 0.025 2 | 0.268 ± 0.01 | -0.020 | 0.021 ± 0.01 |
Table II Analyses exhibiting interferences of the "self-interfering" variety.
wt. % (nominal) |
wt. % (uncorrected) |
wt. % (Eq. 1) |
wt. % (Eq. 2) |
|
| Ba La « Ti Ka (PET) |
Ba 33.15 3 Ti 11.69 |
33.26 ± 0.18 11.71 ± 0.08 |
33.08 11.59 |
33.08 ± 0.18 11.59 ± 0.08 |
| Pb La « As Ka | Pb 59.69 4 As 21.58 |
106.20 ± 0.33 41.38 ± 0.27 |
19.64 6.60 |
61.25 ± 1.97 22.15 ± 1.04 |
1 SRM 1159 includes : Ni 48.2, Fe 51.0, C 0.007, Mn 0.30, P 0.003, S 0.003, Si 0.32, Cu 0.038, Cr 0.06, Mo 0.01
2 SRM 654b includes : Ti 88.974, Al 6.34, V 4.31, Fe 0.23, Si 0.045, Ni 0.028, Sn 0.023, Cu 0.004, Mo 0.013, Zr 0.008
3 Benitoite (BaTiSi3O9) is assumed stoichiometric : Si 20.38, Ba 33.15, Ti 11.69, O 34.896
4 Shultenite (HAsPbO4) is assumed stoichiometric : Pb 59.69, As 21.58, O 18.44. The oxygen concentration was measured at 19.8 wt. % and included in the matrix correction calculations.
References
1. J. V. Gilfrich, L. S. Birks, J. W. Criss, "Correction for Line Interferences in Wavelength-Dispersive X-ray Analysis", in: X-Ray Fluorescence Analysis of Environmental Samples, T. G. Dzubay Ed., Ann Arbor Science Publ., Ann Arbor, (1978), 283.
2. J. J. Donovan, D. A. Snyder, M. L. Rivers, "An Improved Interference Correction for Trace Element Analysis", in: Microbeam Analysis, (1993), 2, 23.
Contact:
John J. Donovan
Department of Geological Sciences
210 Cascade Hall
University of Oregon
Eugene, OR, 97403
(541) 346-4632 (voice)
(541) 346-4692 (FAX)
Back To Department of Earth and Planetary Science Home Page