The analysis of light elements (fluorine - beryllium) present special problems for the microprobe analyst. Some of these problems are technical in substance, relating to the measurement procedure, while others are inherent and are due to physical and chemical effects. The following is just an overview of these concerns. For a more complete treatment the reader is referred to (Bastin and Heijligers, 1986) and (Goldstein, et.al., 1981).
Physical and Chemical Effects
1. Low fluorescent yields from these k-lines compounded by a relatively poor reflectivity of analyzing crystals and low sensitivity of detector systems can result in extremely low count rates. Increasing the beam current can produce unacceptably high deadtime corrections for any metal lines present which may also need to be measured. The use of layered dispersive element (LDE) reflectors can improve things somewhat.
2. Errors in the estimation or accuracy of the take off angle or operating voltage of the microprobe. While slight variations in these parameters normally have a little effect on a typical analysis, due to the very high absorption corrections of low energy x-rays, the effect on the ZAF correction can be much larger for the light elements and can sometimes result is large systematic errors.
3. Errors in the mass absorption coefficients (or MACs) for the x-ray absorption cross sections for these elements are considerable. See Appendix C for a table of MACs for the light elements from a variety of sources. There is considerable disagreement among investigators. Probe for Windows allows the user to enter MACs from any source for re-calculation purposes.
4. Chemical bonding effects can results in large peak shift and/or shape changes to the analytical x-ray lines. In fact the degree of shift and/or shape changes in light element K lines and transition metal L lines can sometimes be related to the degree of oxidation in the compound. But normally these effects are a nuisance to the analyst. In a few instances there has even been documented cases of particular lines being strongly enhanced (Ni La in NiAl) or reduced (B Ka in nickel borides) (Pouchou and Pichoir, 1988).
5. Volatilization of certain light elements such as sodium and fluorine is often the case in glasses and other amorphous samples. See the use of the Volatile element correction for a powerful software correction to remove this effect.
Problems with the Measurement Techniques
1. Higher order interferences from metal lines are everywhere and must be avoided when possible or corrected for when not. The elements Ti, Cr, Mn, Zr and Nb are well known in this respect. Although it would seem appropriate to use pulse-height analysis (PHA) to reduce these interferences it is often found that narrow PHA settings can introduce more problems than they solve. See (Donovan, et.al., 1993). These interferences are especially severe for minor and trace level measurements.
2. Carbon contamination is a serious problem for quantitative analysis of light elements, especially of course, carbon but also the other light elements. Contamination is produced by the polymerization of hydrocarbons at the point of impact of the electron beam. Carbon compounds present may include diffusion pump oils, polishing agents, cleaning solvents, among others. The use of an air-jet has been shown to dramatically reduce carbon contamination. It is suggested that the analyst perform measurements to ascertain the actual carbon contamination rate in their microprobe for each element being analyzed.
3. Trace analysis of light elements is particularly difficult, especially oxygen and carbon. Keeping a metallic sample surface from oxidizing is not a trivial matter. The use of an ion mill inside the probe to remove the very top layer of the sample, just prior to the analysis, if available, would be ideal. Note that the increase in temperature of non-conducting samples can be significant enough to cause additional oxidation of the surface. Trace carbon analyses can be difficult without the use of an air jet to reduce the carbon contamination at the point of impact of the beam.
4. Another problem which has not been adequately addressed is x-ray production in non-conductive samples. Effects on x-ray production are seen even when a conductive coating has been applied, possibly due to internal charge buildup below the conductive layer.
5. The selection of standards is also critical due to the already mentioned peak shift and/or shape changes for light element x-rays. The use of Area Peak Factors (APFs) (Bastin and Heijligers, 1986) can provide the analyst with a practical method for treatment of these effects. Program PROBE supports the use of APF factors for analysis of light elements.
6. Be aware also, that carbide, boride and nitride standards are often not 100 % dense resulting in significant errors in the analysis. If single crystals can be obtained, so much the better.
G. F. Bastin and H. J. M. Heijligers, "Quantitative Electron Probe Microanalysis of Carbon in Binary Carbides," Parts I and II, X-Ray Spectr. 15: 135-150, 1986
J. I. Goldstein, D. E. Newbury, P. Echlin, D. C. Joy, C. Fiori, E. Lifshin, "Scanning Electron Microscopy and X-Ray Microanalysis", Plenum, New York, 1981
This menu allows the user to selectively load empirical APFs (Area Peak Factors) from a supplied ASCII file or data entry.
A powerful feature in Probe for Windows allows the user to select an Area-Peak-Factor (APF) correction for use in correcting x-ray intensities for peak shift and shape changes between the standard and the unknown. This can occur especially with Ka lines of the light elements such as oxygen, nitrogen, carbon and boron. With these elements, differences in the bond energies between say TiC and SiC will produce significantly different peak shapes resulting in systematic errors in the analysis of these materials when only the peak x-ray intensities are used.
For example, when analyzing oxygen and using MgO or Fe2O3 as an oxygen standard, analyses of SiO2 will produce errors up to about 4.5%. This effect is independent of the matrix correction and can be corrected for only by the use of the appropriate APFs.
The APF concept was proposed by Bastin and Heijligers (Bastin and Heijligers, 1986) to provide a simple correction scheme for this effect. It basically requires measuring the ratio of the peak intensity to the integrated intensity between a primary standard to a number of secondary standards on the light element spectrometer used. The wavelength scan feature in Probe for Windows can be used to acquire the peak shape profiles. After correcting for background and removal of extraneous peaks from interfering lines, the APF can be calculated. The calculation of the APF factor is shown below :
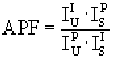
Where :
is the integrated intensity of the secondary standard
is the peak intensity of the primary standard
is the peak intensity of the secondary standard
is the integrated intensity of the primary standard
The peak shape and shift of light element peaks can be easily demonstrated using MgO and SiO2 standard samples. First select a suitable layered dispersive element (LDE) analyzing crystal for oxygen Ka analysis. Tune the spectrometer using the MgO standard and acquire a standard sample for MgO. Assign MgO as the calibration standard for oxygen. Then move to the SiO2 standard and acquire another quantitative standard sample on the SiO2 sample. Note that the analysis of SiO2 using MgO as a calibration standard will result in a low total for the SiO2, somewhere around 96-97 %. This is not an error in the mass absorption coefficient (MAC), and no attempt should be made to correct this problem by entering an arbitrary MAC value.
Instead, the proper APF correction will need to be applied as shown below. Although the values below are relative to Fe2O3, you will note that the APF for MgO is 1.000, which means that these correction factors apply equally well relative to MgO. In the Oxygen Area Peak Factor table below you will note that oxygen in the presence of SiO2 needs to be corrected by a factor of 1.0444 when MgO or Fe2O3 is used a a calibration standard. After entering this APF correction factor for the oxygen channel and re-analyzing, note that the total is now close to 100 %.
It is very important to note that the APF values selected or entered are always measured relative to some standard sample. For example, if measuring C Ka and using Fe3C as the primary standard for carbon, then any C Ka APF values used must be those measured relative to Fe3C. For the same reason, if using APF values for a particular (light) element and one decides to re-assign the standard for that element, the APF values for that element must also be changed to reflect the standard re-assignment. See the section above for information on re-calculating the APF values relative to another standard.
For the above reason it is usually most efficient to simply always use the same standard for each light element analyzed. Typically (in order to utilize the APF values in the supplied EMPAPF.DAT file) these will be :
- Oxygen : MgO or Fe2O3
- Nitrogen : AlN
- Carbon : Fe3C
- Boron : B metal
The APF correction in Probe for Windows will allow the user to enter empirical APF values in each run. The user may enter one or more APF factors for each emitting element although they are generally applied to soft x-ray lines. Note however that even S Ka exhibits peak shift and shape changes when comparing sulfide and sulfate peaks. The APF for each absorber will be summed according to it's weight fraction in the composition and applied to the emitting element counts during the ZAF or Phi-Rho-Z iteration.
If it is desired to correct a complete unknown for peak shape changes, simply perform a wavelength scan on the standard being used for the light element emitter (oxygen, carbon, etc.) and also on the unknown. Calculate the APF using the expression above and from the Analytical | Empirical APFs menu, enter the same APF for all absorbers in the unknown. The program will then sum the APFs which will be the same as the single measured APF. Note that this APF may only apply to a single composition. One can perform additional wavelength scans on other samples to confirm this however.
The APF correction values are defined in the EMPAPF.DAT file in the XRAYDATA sub directory (usually C:\PROBEWIN\XRAYDATA). The file contains some 50 or 60 values that may or may not be applicable, depending on the analyzing crystals and standards available. The user may edit the file using any ASCII text editor such as NotePad or NoteBook to insert their own measurements. Be careful to avoid adding any <tab> characters when editing the file (use space or comma delimited values only). Note that the elements may be in any order although they have been sorted to facilitate editing.
The format of the EMPAPF.DAT file is shown below :
"b" "ka" "c"
1.02 "B4C/B/STE"
"b" "ka" "n" 1.2
"BN/B/STE"
"b" "ka" "al"
1.12 "AlB2/B/STE"
"b" "ka" "al"
1.01 "AlB12/B/STE"
"b" "ka" "si" 1
"SiB3/B/STE"
"b" "ka" "si"
.92 "SiB6/B/STE"
"b" "ka" "ti"
.75 "TiB/B/STE"
"b" "ka" "ti"
.88 "TiB2/B/STE"
"b" "ka" "v" 1
"VB2/B/STE"
"b" "ka" "cr" .9
"CrB/B/STE"
"b" "ka" "cr"
1.1 "CrB2/B/STE"
"b" "ka" "fe"
1.1 "FeB/B/STE"
"b" "ka" "fe"
1.25 "Fe2B/B/STE"
"b" "ka" "co"
1.2 "CoB/B/STE"
"b" "ka" "co"
1.02 "Co2B/B/STE"
"b" "ka" "ni"
1.2 "NiB/B/STE"
"b" "ka" "ni"
1.06 "Ni2B/B/STE"
"b" "ka" "ni"
.98 "Ni3B/B/STE"
"b" "ka" "zr" .8
"ZrB2/B/STE"
"b" "ka" "nb" .8
"NbB/B/STE"
"b" "ka" "nb" .9
"NbB2/B/STE"
"b" "ka" "mo"
.94 "MoB/B/STE"
"b" "ka" "la" .9
"LaB6/B/STE"
"b" "ka" "ta"
.88 "TaB/B/STE"
"b" "ka" "ta"
1.1 "TaB2/B/STE"
"b" "ka" "w" .98
"WB/B/STE"
"b" "ka" "u"
1.04 "UB4/B/STE"
"c" "ka" "b"
1.01 "B4C/Fe3C/WSi/59.8"
"c" "ka" "si"
.933 "SiC/Fe3C/WSi/59.8"
"c" "ka" "ti"
.868 "TiC/Fe3C/WSi/59.8"
"c" "ka" "v"
.873 "V2C/Fe3C/WSi/59.8"
"c" "ka" "v"
.873 "VC/Fe3C/WSi/59.8"
"c" "ka" "cr" .8
"Cr7C3/Fe3C/STE"
"c" "ka" "cr"
.83 "Cr3C2/Fe3C/STE"
"c" "ka" "cr" .8
"Cr23C6/Fe3C/STE"
"c" "ka" "zr"
.88 "ZrC/Fe3C/WSi/59.8"
"c" "ka" "nb"
.79 "NbC/Fe3C/STE"
"c" "ka" "mo"
.82 "Mo2C/Fe3C/STE"
"c" "ka" "hf"
.83 "HfC/Fe3C/STE"
"c" "ka" "ta"
.96 "TaC/Fe3C/STE"
"c" "ka" "w" .97
"WC/Fe3C/STE"
"c" "ka" "w"
1.02 "W2C/Fe3C/STE"
"n" "ka" "si"
1.103 "Si3N4/AlN/WSi/59.8"
"n" "ka" "ti"
.997 "TiN/AlN/WSi/59.8"
"n" "ka" "v"
1.0226 "VN/AlN/WSi/59.8"
"n" "ka" "cr"
1.018 "Cr2N/AlN/WSi/59.8"
"n" "ka" "fe"
1.012 "Fe2N/AlN/WSi/59.8"
"n" "ka" "zr"
.9952 "ZrN/AlN/WSi/59.8"
"n" "ka" "hf"
1.002 "HfN/AlN/WSi/59.8"
"o" "ka" "b"
1.0628 "B6O/Fe2O3/WSi/59.8"
"o" "ka" "mg" 1
"MgO/Fe2O3/WSi/59.8"
"o" "ka" "al"
1.0213 "Al2O3/Fe2O3/WSi/59.8"
"o" "ka" "si"
1.0444 "SiO2/Fe2O3/WSi/59.8"
"o" "ka" "ti"
.9796 "TiO2/Fe2O3/WSi/59.8"
"o" "ka" "cr"
.993 "Cr2O3/Fe2O3/WSi/59.8"
"o" "ka" "mn"
1.0121 "MnO/Fe2O3/WSi/59.8"
"o" "ka" "fe"
.9962 "Fe3O4/Fe2O3/WSi/59.8"
"o" "ka" "co"
1.0133 "CoO/Fe2O3/WSi/59.8"
"o" "ka" "ni"
1.0153 "NiO/Fe2O3/WSi/59.8"
"o" "ka" "cu"
.9946 "Cu2O/Fe2O3/WSi/59.8"
"o" "ka" "cu"
.9943 "CuO/Fe2O3/WSi/59.8"
"o" "ka" "zn"
.9837 "ZnO/Fe2O3/WSi/59.8"
"o" "ka" "ga" 1
"Ga2O3/Fe2O3/WSi/59.8"
"o" "ka" "zr"
.9823 "Y3Fe5O12/Fe2O3/WSi/59.8"
The first column (in the example is "b" for Boron) is the atomic symbol of the emitting element. The second column ("ka" in the example equals Ka) is the x-ray line of the emitter. The third column is the atomic symbol of the absorber element. The fourth column is the actual area peak factor (APF) that has been experimentally measured. The last parameter is a string that contains the conditions under which the APF was measured. For example, the comment "B4C/B/STE" indicates that the peak and integrated intensities for the APF were measured on a B4C (boron carbide) sample, relative to a B (elemental Boron) primary standard, using a Pb Stearate analyzer. The reason that this information is needed is because the APF is a relative measurement (to a standard) and the value is dependent on the resolution (crystal type) used. If a LDE (layered dispersive element) analyzer is used, the 2d of the analyzer should be indicated also as seen in the last two lines of the example.
The first and third columns (emitting atomic symbol and absorber atomic symbol) must be valid element symbols. The second column (x-ray line) must be "ka", "la" or "ma". All element and x-ray symbols must be enclosed in double quotes. The fourth column (APF value) must be a real number greater than 0.0. The comment string must be enclosed in double quotes.
These values can then be loaded from the Analytical | Empirical APFs menu item in Probe for Windows. Note that the comments listed after each APF value can be used to indicate the experimental conditions under which the APF was measured. For consistency sake, the formula of the compound measured is listed first, then the primary reference standard used and finally the analyzing crystal type (and 2d spacing if desired) used. Edit the EMPAPF.DAT file in the XRAYDATA sub directory to add additional APFs from your own measurements.
The following is a short listing of some typical APFs taken from Bastin and Heijligers (1986). Because the factors are spectrometer and crystal dependent these should be used as a guide only.
Oxygen Area Peak Factors (APF)
Relative to Fe2O3 or MgO using W/Si LDE (2d = 59.8)
Oxide |
Area-Peak Factor (APF) |
B6O |
1.0628 |
MgO |
1.0000 |
Al2O3 |
1.0213 |
SiO2 |
1.0444 |
TiO2 |
0.9796 |
Cr2O3 |
0.9930 |
Mn3O4 |
1.0121 |
Fe3O4 |
0.9962 |
CoO |
1.0133 |
NiO |
1.0153 |
Cu2O |
0.9946 |
CuO |
0.9943 |
ZnO |
0.9837 |
Ga2O3 |
1.0000 |
Y3Fe5O12 |
0.9823 |
Carbon Area-Peak Factors
Relative to Fe3C using W/Si LDE (2d = 59.8):
Carbide |
Area-Peak-Factor (APF) |
B4C |
1.010 |
SiC |
0.933 |
TiC |
0.868 |
V2C |
0.873 |
VC |
0.873 |
ZrC |
0.880 |
Nitrogen Area-Peak Factors
Relative to AlN using W/Si LDE (2d = 59.8):
Carbide |
Area-Peak-Factor (APF) |
AlN |
1.000 |
Si3N4 |
1.103 |
TiN |
.997 |
VN |
1.0226 |
Cr2N |
1.018 |
Fe2N |
1.012 |
ZrN |
.9952 |
HfN |
1.002 |
Area Peak Factors and Standard Assignments
Another consideration in assigning standards, concerns the use of Area Peak Factors (APF) for correction of light element peak shift and shape changes. When analysis of light elements is to be performed (typically oxygen, nitrogen, carbon and boron but possibly heavier elements such as silicon, aluminum and sulfur), you need to plan the use of APF corrections for the most accurate results. The actual APF values selected will depend the standard assigned for calibration of the light element.
For example, when analyzing for C Ka and using Fe3C as your carbon standard, your APF value for C Ka in a Cr7C3 matrix might be 0.80. However, if instead, you re-assigned your carbon standard to TiC, you must use APF values relative to TiC rather than Fe3C. If they are available in the Empirical APF database (EMPAPF.DAT), just change the APF values for C Ka. Otherwise you would need to calculate the Fe3C APF values relative to TiC. Some typical Fe3C APF values for C Ka, recalculated relative to TiC and Cr7C3, are shown in the table below :
| APF Relative To : | Fe3C (APF/1.000) | TiC (APF/0.868) | Cr7C3 (APF/0.80) |
Fe3C |
1.000 |
1.152 |
1.25 |
TiC |
0.868 |
1.000 |
1.085 |
Cr7C3 |
0.80 |
0.92 |
1.00 |
G. F. Bastin and H. J. M. Heijligers, "Quantitative Electron Probe Microanalysis of Carbon in Binary Carbides," Parts I and II, X-Ray Spectr. 15: 135-150, 1986
In an attempt to verify Bastin's published oxygen Ka APF values for Al2O3 and SiO2 using the same model instrument (SX51) and analyzing crystal (W/Si 60 A 2d), I ran a series of wavescans on MgO (standard for oxygen), Al2O3 and SiO2. Four wavescans were acquired on each standard at 15 keV, 40 nA, 10 um beam and 200 points with 15 second count time each point using a 1 um stage step every 60 sec.
Using the equation P/I(std) * I/P(unk) to obtain the APF, the following calculations were performed (P/I is the peak intensity divided by the integrated intensity and I/P is the integrated intensity divided by the peak intensity) :
| MgO | Al2O3 | Al2O3 APF | SiO2 | SiO2 APF | |
| #1 (P/I) | 0.000951 | 0.000927 | 1.026 | 0.000890 | 1.068 |
| #1 (I/P) | 1051.6 | 1078.9 | 1123.4 | ||
| #2 (P/I) | 0.000951 | 0.000925 | 1.028 | 0.000889 | 1.069 |
| #2 (I/P) | 1051.3 | 1080.6 | 1124.9 | ||
| #3 (P/I) | 0.000952 | 0.000923 | 1.031 | 0.000890 | 1.070 |
| #3 (I/P) | 1049.9 | 1083.2 | 1124.1 | ||
| #4 (P/I) | 0.000952 | 0.000925 | 1.029 | 0.000889 | 1.071 |
| #4 (I/P) | 1050.3 | 1081.4 | 1125.4 | ||
| Average: | |||||
| (P/I) | 0.0009515 | 0.000925 | 1.0285 | 0.0008895 | 1.070 |
| (I/P) | 1050.8 | 1081 | (1.0213 Bastin) | 1124.5 | (1.0444 Bastin) |
As you can see, my average APF for Al2O3 relative to MgO is 1.0285, while Bastin got 1.0213. For SiO2 I got 1.070 while Bastin got 1.0444. This measurements illustrate the importance of calibrating APFs on the actual instument that they will be used on.
Back To Department of Earth and Planetary Science Home Page