John J.
Donovan
Department of Geology and Geophysics
University of California
Berkeley, CA 94720-4767
and
Tracy N.
Tingle
Center for Materials Research and
Department of Geological and
Environmental Sciences
Stanford University,
Stanford, CA 94305-4045
Keywords : microprobe, quantitative analysis, microanalysis, background correction, atomic number, continuum
Reference
J. J. Donovan and T. N. Tingle, "An Improved Mean Atomic Number Correction for Quantitative Microanalysis" in Journal of Microscopy, v. 2, 1, p. 1-7, 1996
Primary/Corresponding Author
John J. Donovan
Department of Geology and Geophysics
Room 301, McCone Hall
University of California
Berkeley, CA 94720-4767
(510) 642-5459 (voice)
(510) 643-9980 (FAX)
e-mail :
jdonovan@seismo.berkeley.edu
jdonovan@garnet.berkeley.edu
Abstract
Quantitative EPMA (electron probe microanalysis) intensity measurements require an accurate correction for the x-ray continuum (or background) created by the bremsstrahlung effect from the primary electron beam. This x-ray continuum, as measured on a wavelength-dispersive spectrometer at any particular wavelength, is primarily a function of the mean atomic number of the material being analyzed. One can calibrate the dependence of the continuum on mean atomic number by measuring and curve fitting the x-ray intensities at the analytical peak in pure elements, oxides and binary compound standards, that do not contain any of the analyte nor any interfering elements, and use that calibration to calculate the x-ray background correction. For unknown samples, the mean atomic number is determined from the elemental concentrations calculated by the ZAF or f(rz) matrix correction, and the fit regression coefficients are used iteratively to calculate the actual background correction. Over a large range of mean atomic number we find that the dependence of the continuum intensity on mean atomic number is well described by a second-order polynomial fit. In the case of low energy x-ray lines (<1-2 keV), this fit is significantly improved by correcting the x-ray continuum intensities for absorption. For major and most minor element analyses, the improved mean atomic number background correction procedure presented in this paper is accurate and robust for a wide variety of samples. Empirical mean atomic number background data are presented for a typical 10-element silicate and a 15-element sulfide analytical setup that demonstrate the validity of the technique as well as some potential limitations.
Introduction
In quantitative x-ray microanalysis, the intensity of characteristic x-rays must be corrected for the background of continuum x-rays over which it is measured. The most rigorous method involves measuring the background on either side of the analytical peak (referred to here as the off-peak method), interpolating to the intensity beneath the peak, and then subtracting that value from the peak intensity. Commonly, the off-peak positions are chosen to be symmetrical about the peak or otherwise to avoid spectral interferences, and the interpolation is based on a linear fit between the two off-peak intensity measurements.
The intensity of the continuum (Ic) is a function of the mean atomic number (Zmean) of the sample, thus providing the basis for the alternative background correction procedure described here. The principal advantage of this method, which we refer to as the mean atomic number (MAN) background correction procedure, is that one only needs to measure the analytical peak intensity, thus saving considerable time and spectrometer motion during the course of analysis. The principal disadvantage is that the precision of analysis is reduced, somewhat for minor (< 0.1 weight percent) and even more for trace elements (< 0.01 weight percent).
Background corrections methods based on the mean atomic number effect were originally utilized by many investigators, seeking to provide a background correction for x-ray monochromaters, which due to their fixed nature are unable to measure off-peak intensities. These early attempts, in the use of a MAN background correction, typically utilized a constant background subtraction, determined by simply measuring the continuum on a standard with a similar mean atomic number to that of the unknown, that which did not contain the analytical element. Later, more sophisticated methods were developed by others (I. S. E. Carmichael and J. McGee, personal communications) that employed a linear interpolation between two or more continuum intensity measurements, and derived an approximate mean atomic number for the unknown sample, by summing the k-ratios of the unknown sample.
We propose an improved MAN background correction procedure based on a calibration curve determined by measuring the on-peak intensities of simple metal and oxide and binary compound standards, covering the range of mean atomic number of both the unknowns and the standards (that do not contain the element of interest). The intensities used to determine the calibration curve are corrected for absorption of the continuum and fitted to a second-order polynomial. During the analysis of unknowns, the background calibration is used in an iterative fashion along with the ZAF or f(rz) matrix correction to determine the composition and hence the mean atomic number of the sample. At the same time, the background for the unknown sample is calculated from the measured functional relationship between Ic and Zmean and subtracted from the unknown peak intensity, until the differences in the calculated background correction converge to a small value.
We present data obtained for a typical 10-element silicate and a 15-element sulfide analysis that demonstrate the importance of correcting the background intensities for absorption of the continuum. We further show that there is no significant reduction in analytical precision for major and minor elements where the peak-to-background (P/B) is greater than 10.
Mean Atomic Background Correction Procedure
Theoretical Basis
Bremsstrahlung (literally "braking radiation") forms the continuum background against which the intensity of characteristic x-rays must be measured in a quantitative EPMA. The intensity of the continuum increases with increasing atomic number due to the greater intensity of the Coulombic field in the core shells of heavier atoms. Kramers (1923) described the intensity of the continuum, Ic, at any wavelength l as:
Ic (l) ~ iZmean[(l /l min) - 1] equation 1
where i is the electron current (which is proportional to the beam current), lmin is the Duane-Hunt or short wavelength limit, and Zmean is the mean atomic number of the sample. Further development by Fiori et al. (1976) leads to the following equation for the intensity of the continuum:
Ic (l) = (W/4p) fl Pl kl iZmean [(l /l min) - 1] equation 2
where W is the detector solid angle, fl is the absorption factor for the continuum (representing the probability that a continuum x-ray of wavelength l will be absorbed in the material), Pl is the detector efficiency for x-rays of wavelength l, kl is Kramers’ constant.
The difficulty of evaluating Pl and kl has been noted (Goldstein et al., 1981), and the approach taken here is to treat them as constants at any given l and include any dependence on atomic number in Kramers’ constant in a second-order polynomial regression of measurements of Ic (l) as a function of Zmean. As will be shown, over small ranges of Zmean, Ic is a linear function of Zmean as expected.
Continuum Absorption Correction
It is also necessary to correct for the absorption of continuum x-rays (fl in equation 2 above) in the material of interest. As will be shown, this approach significantly improves the regression of Ic versus Zmean. The absorption correction is easily performed by utilizing the absorption factor of the ZAF or f(rz) correction procedure (Philibert-Duncumb-Heinrich equation) during the calculation of the background. We have also used the equation of Yakowitz et al. (1973) to calculate fl, but we found better agreement (regression fits) over a larger range of Zmean using the Philibert-Duncumb-Heinrich equation.
Iteration Procedure
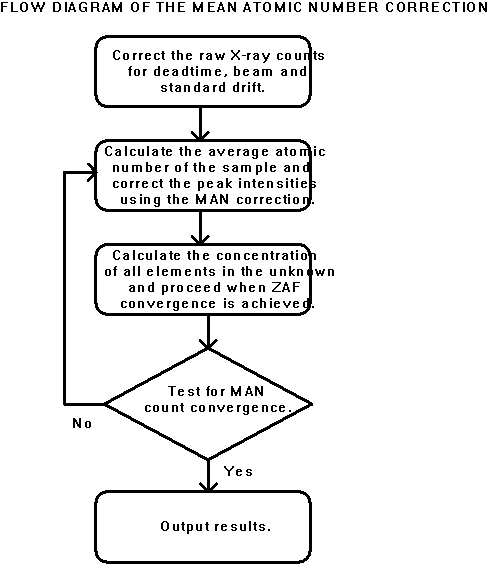
The MAN background correction algorithm was combined with the CITZAF f(rz) matrix correction algorithms (Armstrong, 1988) in the PROBE acquisition and analysis program (Donovan et al., 1990; 1992). As shown schematically in Figure 1, a double iteration loop is utilized in which the inner loop performs the ZAF or f(rz) elemental concentration calculation, and the outer loop performs the MAN background correction based on the mean atomic number derived from the element concentration calculation. The outer iteration loop is also used for quantitative correction of other compositionally dependent effects, such as spectral interferences (Donovan et al., 1992), light element area peak factors (Bastin and Heijligers, 1986), and element volatilization and electromigration (Neilsen and Haraldur, 1981).
The MAN background correction is performed as follows: First, on-peak intensities are acquired on standards that do not contain any of the analyte nor any elements with interfering spectral lines. The measured intensities are corrected for absorption by multiplying by the absorption factor obtained from the standard k-factor calculation. Second, the Ic-Zmean data are regressed, and the regression coefficients are stored for subsequent calculations.
Measured unknown sample peak intensities are corrected for background as follows: The continuum-corrected background intensity is calculated from the mean atomic number determined from the concentrations obtained during the previous iteration of the ZAF f(rz) matrix correction using the regression coefficients determined above. An arbitrary mean atomic number is assumed in the first iteration; notwithstanding, the calculated background typically converges to within 0.1 counts per second after only 2-3 iterations. This is true even when the absorption correction factor is large. Lastly, the calculated continuum-corrected background intensity is divided by the absorption factor calculated for the unknown sample and subtracted from the measured peak intensity.
If instrument or spectrometer drift is thought to pose a problem, one can acquire additional MAN background data sets. A linear interpolation method is employed to calculate a drift-corrected MAN calibration curve. In practice, the x-ray background drifts very little in a modern microprobe, and drift correction of the MAN background data is seldom necessary.
Experimental Results
Typical 10-element silicate analysis
Mean atomic number (MAN) backgrounds were measured on 42 metals, simple oxides and binary compounds on the 5-spectrometer JEOL 733 electron microprobe at Stanford University. Table 1 shows the instrument configuration for this typical silicate setup. Figure 2 shows the MAN background data uncorrected and corrected for continuum absorption as described above.
For the range of mean atomic numbers encountered in a typical silicate analysis (Z=10-20), the polynomial fit to the continuum absorption-corrected intensities shows an excellent correlation (R = 0.97 for all elements; Fig. 2). In all cases these fits were better than a polynomial fit to the uncorrected data. As expected, the uncorrected data for the lighter elements (with the larger absorption coefficients) showed the most significant deviations from a simple linear or polynomial fit.
The observed deviation from the polynomial fit was used to estimate an approximate concentration error for each sample analyzed. For Na, Mg, Al, Si, K and Ca, that error is less than 0.02 weight percent, and for Ti, Cr, Mn and Fe, that error is less than 0.03 weight percent. This error is of approximately the same order as expected (based on x-ray counting statistics) when one is performing an off-peak background correction.
15-element sulfide analysis
The same metals, oxides and binary compounds above were analyzed using a 15-element setup as shown in Table 2. Figure 3 shows the x-ray intensities for those materials uncorrected and corrected for absorption of the continuum.
The potential range of mean atomic number that may be encountered in a sulfide analysis is greater than that for silicates and most oxides, Z = 21 (MnS) -73 (PbS). The polynomial fits to the continuum absorption-corrected intensities for the transition metals x-ray lines again show excellent correlation. In fact, there is little difference between the corrected and uncorrected intensities because the continuum absorption correction for these elements is small. The same fits for Sb, As, Ag, Pb, Hg and Bi are also good, whereas the fits for S, Au, Pt show considerable scatter. As shown above for the silicate setup, in all cases the continuum-corrected data yield better polynomial fits than the uncorrected data. The approximate concentration errors, estimated from the individual deviations from the polynomial fits, are as follows: S, Mn, Fe, Co, are less than 0.05 weight percent. Co, Ni, Cu, Zn, Ag, As and Sb are less than 0.07 weight percent. For the following measurements using Ma spectral lines, the analytical precision using the MAN method for Hg is of the order of 0.15 wt. %, and for Pt and Au are of the order of 0.5 wt. %.
The poor regression fits for Au and Pt are not well understood. It could be interpreted as discrepancies in the mass absorption coefficients or small, but significant spectral interferences.
Discussion
The data presented above demonstrate that it is possible to calibrate rather precisely the effect of the mean atomic number on the intensity of the x-ray background. The calibration is significantly improved for low energy (< 1-2 keV) spectral lines by correcting for absorption of the continuum in the material. The iterative calculation of the x-ray background using regression coefficients derived from the empirical calibration of Ic-Zmean and calculated elemental concentrations further improves the accuracy of the method.
The magnitude of the error to be expected using the mean atomic number background correction presented here is not significant for major and most minor element analyses. As an example, consider an analyte peak intensity of 10,000 counts with a peak/background ratio of 100 as typical of that for a major element. The peak counting error is comparable to the background counts, and so uncertainties in the calculation of the background from the Zmean of the sample are trivial. Consider now the case of a minor element, where the peak/background is 10, and the peak intensity is 1000 counts. A 10-20% uncertainty in the calculation of the background from its Zmean amounts to a 1-2% error in the calculated analyte peak intensity. However, as the peak/background ratio decreases below 10, uncertainties in the calculation of the background become more significant, and the analyst must be concerned with the accuracy of minor element concentrations thus determined.
The primary benefit of the MAN background correction procedure is reduced acquisition time. During the acquisition of large data sets (e.g. extended stage traverses or quantitative imaging), the time required for the measurement of off-peak intensities and for associated spectrometer motion is eliminated. Not having to measure off-peak backgrounds may also be useful when analyzing samples that are easily beam-damaged or contain volatile elements, because x-ray intensities can be acquired before significant sample degradation occurs.
Such a background correction procedure is essential where wavelength-dispersive monochromators are employed for quantitative analysis, since monochromators cannot be adjusted to measure off-peak intensities. Furthermore, off-peak interferences do not need to be considered, eliminating the need to perform wavelength scans to ensure that the off-peak positions are free of interferences. The MAN background method also may be useful in situations where the background region is highly non-linear, as is often observed at low-theta spectrometer angles.
There are certain potential problems, however, with the MAN background correction method that should be noted. First , the accuracy of the MAN correction will be compromised if the composition of the sample is not known with sufficient accuracy, because the Zmean, and hence the subtracted background, is calculated from the measured composition. Errors in the calculation of the composition, as may occur in samples containing a significant quantity of an element that was not analyzed or one or more volatile elements, inaccurate matrix corrections, or interferences, will compromise the background correction. For this reason it is important to (1) either analyze, calculate by difference/stoichiometry, or specify the concentration of all elements known to be present in the sample; (2) use a modern ZAF or f(rz) matrix correction; (3) quantitatively correct for interferences.
Finally, the standards used for the MAN calibration must be pure and uncontaminated by the element of interest. This can sometimes be difficult to achieve. For example, it is difficult to employ MAN background corrections for the analysis of oxygen, because there are very few substances that do not contain oxygen and do not oxidize to at least some degree.
Conclusion
The MAN background correction has been used extensively in the microprobe laboratories of both Berkeley and Stanford, on a large variety of samples and under various analytical situations, encompassing the fields of geology, chemistry, physics, material science and anthropology. While the MAN background method is not applicable in all cases, (e.g. trace element analysis), we find that for most samples, the MAN background correction can provide an accurate yet rapid background correction for wavelength dispersive spectrometer data, provided that the analyst makes sufficient effort to carefully calibrate the continuum, correct for absorption of the continuum, and obtain accurate compositions for calculation of the mean atomic number of the unknown sample.
Acknowledgments
The authors would like to thank I.S.E. Carmichael and B. Evans for their early efforts in developing the MAN background correction method and J. T. Armstrong for his helpful discussions and suggestions for improving the accuracy of the MAN background correction method. R. E. Jones assisted with the collection of the data presented in this paper.
References
Armstrong, J. T. (1988) Quantitative analysis of silicates and oxide minerals: Comparison of Monte-Carlo, ZAF and Phi-Rho-Z procedures: p. 239, in: Proc. Microbeam Analysis Society, ed. by D. E. Newbury, San Francisco Press, San Francisco.
Bastin, G. F., and Heijligers, H. J. M. (1986) Quantitative Electron Probe Microanalysis of Carbon in Binary Carbides, Parts I and II, X-ray Spectrom., 15, 135-150.
Donovan, J. J. and Rivers, M. L. (1990) PRSUPR- A PC Based Automation and Analysis Software Package for Wavelength-Dispersive Electron-Beam Microanalysis: p. 66, in: Proc. Microbeam Analysis Society, ed. by J. R. Michael and P. Ingram, San Francisco Press, San Francisco.
Donovan, J. J., Rivers, M. L. and Armstrong, J. T. (1992) PRSUPR: Automation and Analysis Software for Wavelength Dispersive Electron-beam Microanalysis on a PC, Amer. Min., 77, 444.
Donovan, J. J., Snyder, D. A. and Rivers, M. L. (1993) An Improved Interference Correction for Trace Element Analysis, Microbeam Analysis, 2, 23-28.
Fiori, C. E., Myklebust, R. L., Heinrich, K. F. J., and Yakowitz, H. (1976) Anal. Chem., 48, 172.
Goldstein, J., Newbury, D., Echlin, P., Fiori, C., and Lifshin, E. (1981) Practical Techniques of X-ray Analysis: p. 399, Chap. 8, in: Scanning Electron Microscopy and X-ray Microanalysis, Plenum, New York.
Kramers, H. A. (1923) Phil. Mag., 46, 836.
Nielsen, C. H., and Haraldur, S. (1981) Quantitative Methods for Electron Microprobe Analysis of Sodium in Natural and Synthetic Glasses, Amer. Min., 66, 547-552.
Yakowitz, H., Myklebust, R. E., and Heinrich, K. F. J. (1973) National Bureau of Standards Technical Note 796, United States Government Printing Office.
Figure 1: Flow diagram of the MAN background correction presented in this study.

Figure 2: Mean atomic number background data for metals, oxides and simple binary compounds. Open circles represent the uncorrected intensities for each line measured (Ti and Cr are not shown), closed symbols represent the intensities corrected for continuum absorption as described in the text. The solid line represents the second-order polynomial best-fit to those data. The inverse of the absorption factor (solid line) shows the expected trend of the background data (without the increase in the Bremsstrahlung with increasing atomic number). For Na, Mg, Al and Si the absorption of the continuum by the various materials can be seen in the uncorrected data.
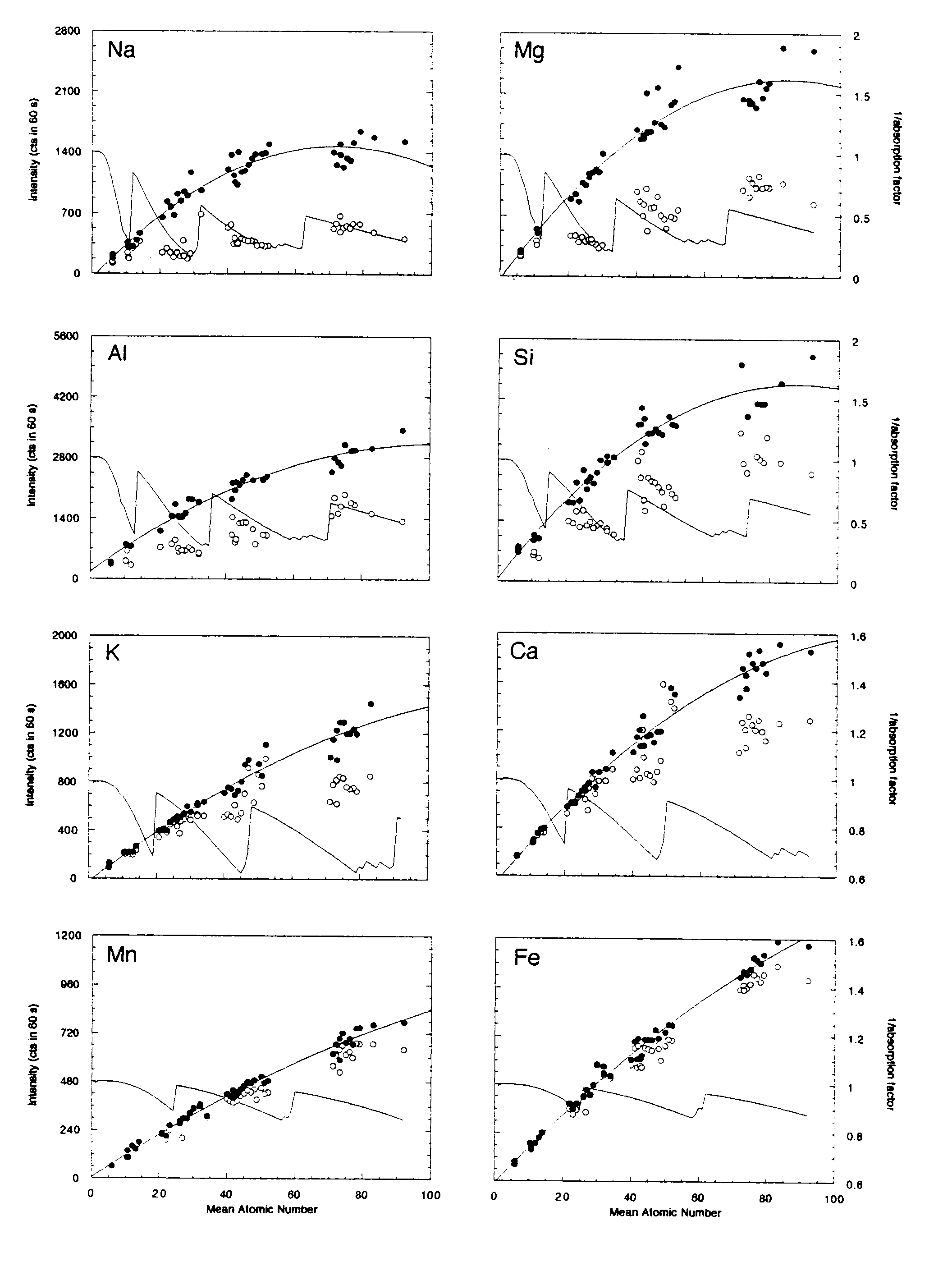
Figure 3: Mean atomic number background data for metals, oxides and simple binary compounds. Open circles represent the uncorrected intensities for each line measured (Cu, Zn, Fe, Mn, Hg, Pb and Bi are not shown), closed symbols represent the intensities corrected for continuum absorption as described in the text. The solid line represents the second-order polynomial best-fit to those data. The inverse of the absorption factor (solid line) shows the expected trend of the background data (without the increase in the Bremsstrahlung with increasing atomic number). As noted in the text, the continuum corrected data measured at the transition metal emission lines show excellent regression fits. The fits for the measurements at the lower energy S, Au and Pt emission lines in high Z materials are not as good, possibly due to discrepencies in the mass absorption coefficients or small but significant spectral interferences.
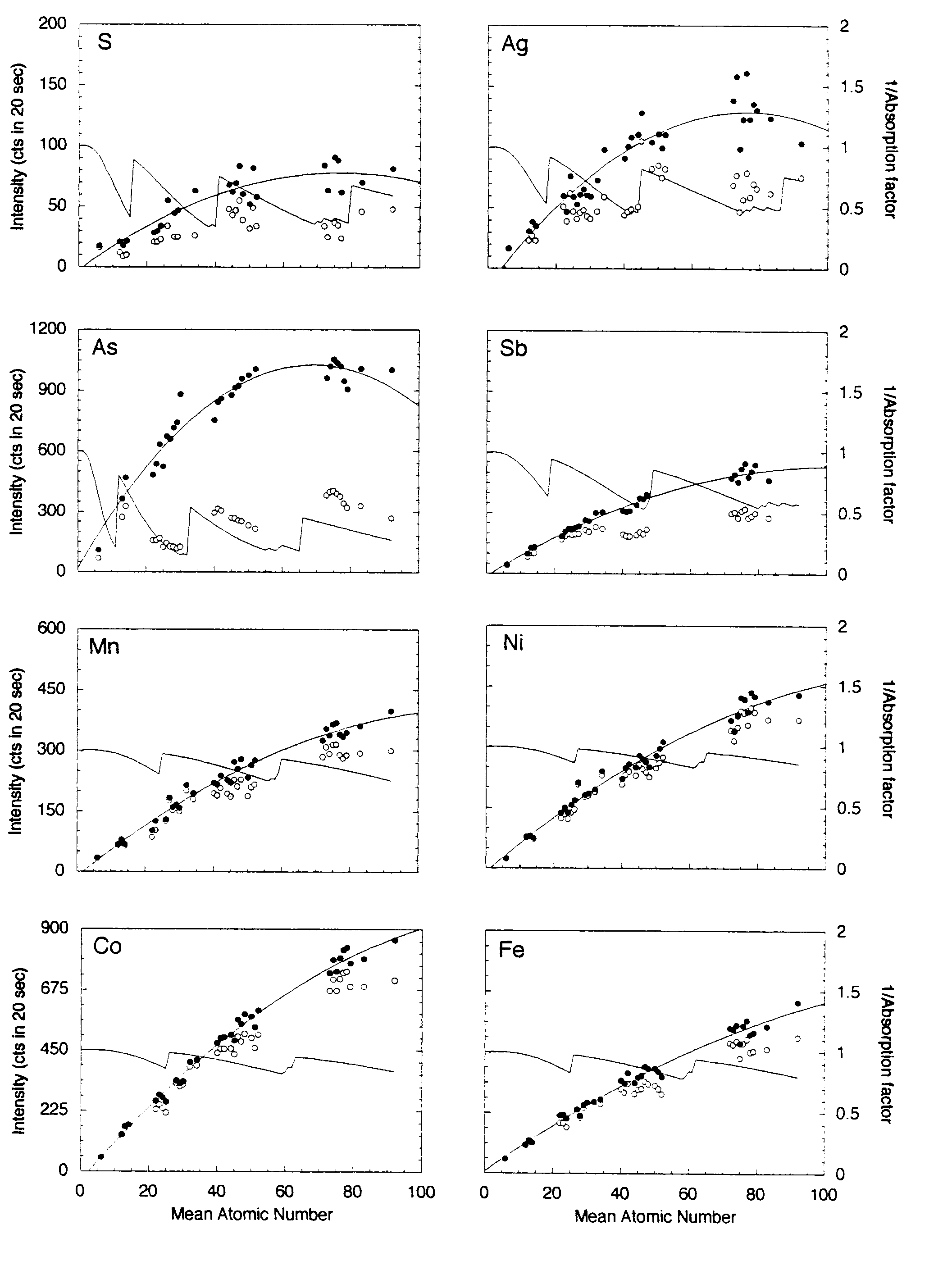
Table I
Instrument configuration for 10-element silicate setup for data shown in Fig. 2. Accelerating voltage was 15 KeV and the take-off angle was 40°. |
||||||
Element |
X-ray line |
Analyzing Crystal |
Detector |
|||
Na |
ka |
TAP |
Gas-flow thin window | |||
Mg |
ka |
TAP |
Gas-flow thin window | |||
Al |
ka |
PET |
Gas-flow thin window | |||
Si |
ka |
PET |
Gas-flow thin window | |||
K |
ka |
PET |
Sealed Xe | |||
Ca |
ka |
LiF |
Sealed Xe | |||
Mn |
ka |
LiF |
Sealed Xe | |||
Fe |
ka |
LiF |
Sealed Xe | |||
Ti |
ka |
LiF |
Sealed Xe | |||
Cr |
ka |
LiF |
Sealed Xe | |||
Table II
Instrument configuration for 15-element sulfide setup for data shown in Fig. 3. Accelerating voltage was 20 KeV and the take-off angle was 40°. |
||||||
Element |
X-ray line |
Analyzing Crystal |
Detector |
|||
S |
ka |
PET |
Gas-flow thin window | |||
Mn |
ka |
PET |
Sealed Xe | |||
Fe |
ka |
LiF |
Sealed Xe | |||
Co |
ka |
LiF |
Sealed Xe | |||
Ni |
ka |
LiF |
Sealed Xe | |||
Cu |
ka |
LiF |
Sealed Xe | |||
Zn |
ka |
LiF |
Sealed Xe | |||
As |
la |
TAP |
Gas-flow thin window | |||
Ag |
la |
PET |
Gas-flow thin window | |||
Sb |
la |
PET |
Gas-flow thin window | |||
Pt |
ma |
TAP |
Gas-flow thin window | |||
Au |
ma |
TAP |
Gas-flow thin window | |||
Hg |
ma |
PET |
Gas-flow | |||
Pb |
ma |
PET |
Gas-flow | |||
Bi |
ma |
PET |
Gas-flow | |||
Back To Department of Earth and Planetary Science Home Page