Chapter 12: Solids What are Solids? We know what we mean when we say something is a solid. We recognize a bar of lead, a rock (olivine), a crystal, a wall are solids, and that the ocean is not solid, the air in this room is not solid, and so on. In this Chapter, we consider what a solid is and some properties of solids. There are two types of solids, ones similar to ones shown in the left, are known as crystalline solids and are things like metals and other regular solids. The ones presented on the right are known as amorphous solids such the obdisian glass and ordinary window glass. The bottom schematic in each panel shows crystalline solids which have long-range order (very nice regular structure) while amorphous solids do not show large-range order.

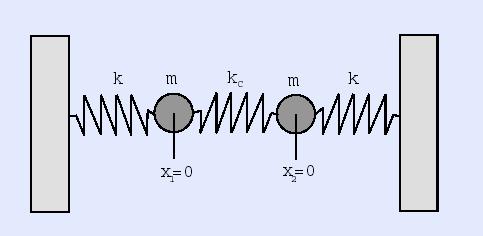
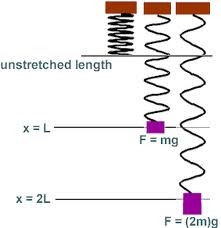
What makes things solids? Is it the chemical make-up of the object (the elements out of which it is composed) or is it something else? (We discuss this later in more detail when we talk about phase changes in the Heat and Thermodynamics secetion, but it is clearly not determined by the chemical make-up of the material as water exists as a solid (ice), a liquid (the oceans), and as a gas (steam).) Crystalline solids solid show regular structures where the atoms, molecules, nuclei, or ions are held rigidly in place, free only to vibrate about their locations. In amorphous solids, the atoms, molecules, nuclei, or ions are maintained in a structure but the structures can distort as the materials are able to flow (e.g., glass will flow); this motion is in addition to vibrations. In both cases, however, the particles interact through electrical forces where we know that the strength of the force falls off with distance. The particles thus try to arrange themselves so that the average electrical repulsion between them is minimized and so settle into distinct structures. In some solids, the electrons are able to migrate through the structure while in others, the electrons are bond more tightly to the individual sites in the structure. In the first case, heat and electrical charge (current) can flow easily through the solid while in the latter case, heat and electrical charge will not flow easily.

Tension and Compression When a solid is shortened, it is under compression When a solid is stretched, it is under tension The strength of the tension and compression are measured by the stress, the tension and/or compression force over the cross-sectional area of the beam. How strongly a material resists compression and tension depends on the details of the material. Despite this, we can make general observations about tension and compression and see applications of the ideas in our everyday lives. In the top right panel, we see that when we bend a material, there is tension (upper surface) and compression (lower surface). In between, there is a layer which is neither stretched nor compressed, the neutral layer (or axis). In the bottom right panel, we see two bends, the same except for orientation. The top configuration is where the weight is supported by tension. In the bottom configuration the weight is supported by compression.

Bridges and Arches The simple beam above is easy to amke, but cannot be made very long before stress causes it to fail. The stress arsies from tension/compression of the beam, the supports tend mainly to hold the beam up and not give it structural support. There are ways to make bridges stronger; one is to divert the stress into a stronger element or to dissipate the stress by spreadiing it out over a larger area.

Directs the stress into the supports

uses cables and pillars to absorb stresses

I Beam Steel is a rigid substance and can profitably be used as supports for large structures. We an more efficiently make beams as suggested by the right. Because the neutral layer carries little stress while the upper and lower surfaces carry the tension and compression, we can make a beam whose cross-section is shaped like an I (as shown to the right). This configuration is nearly as strong as a solid beam but requires much less material and is much lighter.

	Catenary An interesting shape is known as a catenary. This particular shape is that which a flexible chain, rope, or what not is held at its end and allowed to hang. The shape assumed is such that the tension and compression follow the shape of the curve. This is the most efficient shape to divert tension/compression into a stronger structure.

Scaling Laws and Giant Ants

THEM (1954)

Surface Area versus Volume Recall the relationship between stress and tension/compression. To lower the effects of tension/compression, we can try and spread it out which lowers the stress but leaves the tension/compression the same. It is the stress that is important. This is why scaling is important. Let's consider the scaling exhibited by the three large blocks of cubes to the right. The first block sets the stage. There is 1 cube in the block and so the force that results from gravity is determined by 1 cube. The compression arising from the gravity is spread over the bottom face of the 1 cube. The second block of cubes is doubled in size, and contains 8 cubes ===> the force on the block that arises from gravity is 8 times larger. The compression is now delivered to the the bottom of the block. The stress is then 2 times as large for the 1 cube block. The largest block is 3 x 3 x 3 cubes and is then composed of 27 cubes ===> the force that arises from gravity is 27 times larger than for the single cube block. The compression that arises from gravity is spread over the 9 cube faces on the bottom of the blockand the stress is now 27/9 (=3) times larger than for the single cube block. The simple example shows that as we proportionately make the blocks larger, the resultant stress actually gets larger and the successively larger blocks become more stressed and thus more likely to collapse. If an ant is scaled up in size proportionately to a monster size, it would likely not be able to support itself. To make an ant monster-sized requires that we also increase the relative size of its supports (its limbs) to support its increased mass (much as elephant legs are not as delicate as ant legs).

Elephants