Chapter 13: Liquids How do Liquids Compare to Solids? We know what we mean when we say something is a solid. We recognize a bar of lead and a rock (olivine) are solids, and that soft drinks, the oceans, and rivers are liquids, and so on. In general terms, we recognize that solids are rigid and/or malleable structures while liquids can flow. (Recall the comment about amorphous solids in this case; Are amorphous solids, solids or liquids?) In this Chapter, we consider how liquids differ from solids, in a physical sense, and some properties of liquids in everyday life. In the top left we see two examples of water (the molecule composed of two hydrogen atoms and one oxygen atom, H2O). To the left, the bottom compares two forms of water. The right hand model shows the well-structured solid form of water, ice, and the left hand model shows a more disorgainized collection of water molecules, a liquid. Interestingly, water expands when it goes from liquid to solid and liquid water has a density of 1 gram per cubic centimeter (1 gram per sugar cube) while solid water (ice) has a density of 0.92 grams per cubic centimeter (0.92 grams per sugar cube)! Solid water is less dense than liquid water which, as we point out later, means that ice floats in liquid water (see the iceberg to the left).

What makes things liquids? In a solid, the interaction between the molecules or ions is very strong and forces them to settle into a rigid structure where they arrange themselves to try and minimize this interaction. We can break down this structure by heating the solid (raising the temperature of the solid) which causes the molecules and ions to start to vibrate faster (to gain kinetic energy). Eventually, this motion allows the molecules and ions to overcome the electrical interactions with their neighbors allowing them to break free of the rigidly defined structure. The molecules and ions are free to start moving. In a liquid, although able to move, the molecules and ions are still not completely free as they still feel the pull of their neighbors. The molecules and ions tend to move but they do not change their volume (the total amount of space which they occupy--however, recall water). As we note later, for a gas, the particles are essentially able to move freely over space.

Atmospheric Pressure and Pressure Underwater Atmospheric pressure arises from the weight of the air sitting above the observer. The mass of air in the column above the head of the observer (see the upper panel on the right) is pulled down by the gravity of the Earth and exerts a force (and pressure) on the observer. At the surface of the Earth the pressure is 14.7 pounds per square inch (1 atmoshphere, 101,000 Pascals, 1 kPa, 1 bar). At higher altitudes, less air sits above an observer and so there is a smaller atmospheric pressure (see the bottom panel on the right). 14.7 pounds per square inch is a lot. A shot put weighs 16 pounds. Why don't we feel this pressure?

Pressure Underwater The pressure underwater works the same as for atmospheric pressure. The pressure exerted underwater depends on the amount of water overhead. The density of water is about 1 gram per cubic centimeter, which is around 800 times that of air so that the pressure underwater changes much more quickly with depth than the atmospheric pressure changes with height. By a depth of 32.8 feet (around 10 meters), the water above the fish leads to a pressure of 1 atmosphere or 101,000 Pascals (101 kPa). At this depth, however, this is not the total pressure because we excluded the pressure exerted by the atmosphere. The total pressure at this depth is that due to the water, 1 atm, and that due to the atmosphere, 1 atm, for a total pressure of 2 atm, twice that at the surface of the ocean where the pressure felt is dominated by the atmospheric pressure. Water is nearly incompressible (cannot squeeze or make it expand easily [by changing the pressure] and so water's density does not change with depth). This means that for every change of 32.8 feet (or ~10 meters) in depth, the pressure increases by 1 atm (101 kPa). This is remarkable. The rate at which the pressure increases as one descends in the ocean, does not depend on the depth. At a depth of 1,000 meters then, the pressure a fish feels is around 100 times the pressure that it feels at the surface of the ocean. The pressure at 1,000 meters is huge, it corresponds to a pressure of around 1,470 pounds per square inch squeezing the fish. As a sobering comment, Venus is the essentially the Earth's twin in that it has a mass roughly the same as that of the Earth, a diameter roughly the same as that of the Earth, and basic composition and placement in the Solar System roughly the same as that of the Earth but, today, has a surface temperature greater than 800 Farenheit (480 Kelvin) and an atmospheric pressure at its surface of 90 atmospheres (9,000 kPa). This is like living at a depth of 900 meters in the Earth's oceans. This is remarkable. (The sobering aspect of this is that given the strong similarity between the basic natures of Earth and Venus, why are they so different today?)

Water Seeks its Own Level In the middle panel, a U-tube is set-up where the water levels differ in each arm. In the right column the pressure produced at the bottom of the U is due to the atmosphere plus the overalying water. In the left column, there, again, is atmospheric plus now a deeper layer of water and so the pressure at the bottom of the U is greater than that produced by the right column. The consequence of this is clear. [Comment--the pressure at a given depth is the same, regardless of the shape of the container.] Now, what about the more complex system on the far right, Pascal's Vase? What happens if liquid is poured into the vase?

Buoyancy and Flotation We next consider buoyancy and some examples of buoyancy. In the left hand panel below, a rock is submerged in a body of water. Will the rock float, sink, or maintain its depth? To determine what happens, we must consider the forces acting on the rock. In the middle panel, we illustrate the effects of pressure. The bottom of the rock is at greater depth than is the top of the rock and so feels a larger pressure due to the surrounding water. The upward push exceeds the downward push and the net force is the buoyancy. To determine the fate of the rock we determine the downward gravitational force. if the force of gravity exceeds the upward push due to to pressure, the buoyancy, then the rock sinks if the force of gravity exceeds the upward push due to to pressure, the buoyancy, then the rock rises (moves upward) if the forces are equal, then the rock maintains its position The general result which will be argued later is that: If the density of the rock is larger than the density of the liquid (in this case water) then the rock will sink. If the density of the rock is smaller than the liquid then the rock is buoyant and will rise. If the density of the rock is the same as the liquid then the rock floats neither rising nor sinking.

Archimedes' Principle Archimedes' treatise On floating bodies states that: Any object, wholly or partially immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object (Archimedes of Syracuse) with clarifications that for a sunken object, the volume of displaced fluid is the volume of the object, and for a floating object on a liquid, the weight of the displaced liquid is the weight of the object. In short, buoyancy = weight of the displaced liquid. If the displaced weight is the same as the object, then buoyancy balances gravity and the object feels neither an upward or downward push If the displaced weight is larger than the object's weight, then buoyancy overcomes gravity and the object rises If the displaced weight is smaller than the object's weight, then buoyancy cannot overcome gravity and the object sinks This translates to the relationship between the density and sinking/rising/floating given above.

density of typical rock in crust, ~ 3.3 gram per cubic centimeter

density of pumice < water, density of obsidian 2.6 gram per cubic centimeter

density of clownfish fish ~ same as water

Flotation From Archimedes' treatise On floating bodies, proposition 5, states that: Any floating object displaces its own weight of fluid (Archimedes of Syracuse). Although made of metal, the interior of the buoy is hollow and so its density is low allowing it to float.

even if the ship is steel, the relevant density must consider the volume of the ship interior to its outer skin.

Supertanker: DWT 318,000 tons, but floats!

Hydraulics For a closed U-tube, where the two mouths have different sizes (different areas), we can find an interesting result. To understand what happens, consider Pascal's Principle: Pressure applied to an enclosed fluid is transmitted undiminished to every part of the fluid, as well as to the walls of the container. So, if I place a weight on the left hand arm of the U-tube it leads to an increased pressure. This increased pressure is transmitted through the entire U-tube so that there is an increased pressure on the right hand mouth of the U-tube as well. This has an interesting consequence. Because the area of the right hand mouth is greater than the left hand mouth, the total applied force on the right will be larger than the applied force on the left The force is multiplied! A large weight can be supported by a small weight in this U-tube.

An interesting application of this result is the hydraulic lift. The important point is that pressures must balance (the applied forces per area) not the applied forces themselves.. If the mouths of the U-tube differ in size from arm-to-arm, then the total force applied to the smaller area arm needed to raise the car will be smaller than the total weight of the car supported by the larger area arm. With only a moderate applied force, a very heavy object can be lifted. The catch is that as the person on the left mush push the fluid much farther than the heavier object is rasied. Regardless, however, heavy objects can be lifted with only moderate applied forces.

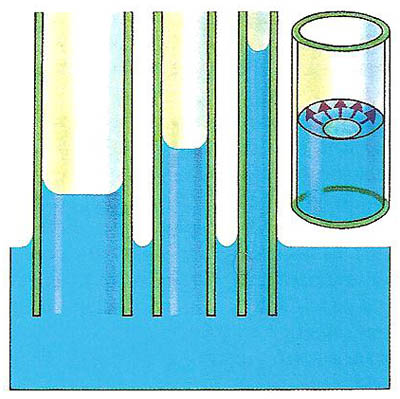
Surface Tension In a liquid, the ions or molecules attract each other (known as cohesion) for the like particles in the liquid. In the body of the liquid because the particles are all around the this attraction tends to average out. At the surface, however, the cohesion pulls the molecules into the liquid, trying to contract the surface. This inward pull is the Surfae Tension. Drop Formation Capillarity Menisci