 Violin
Grand Piano
|
|
 Violin
Grand Piano
|
|
|
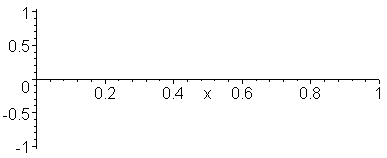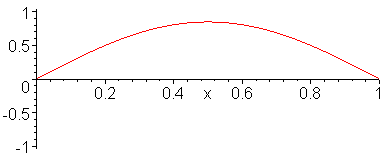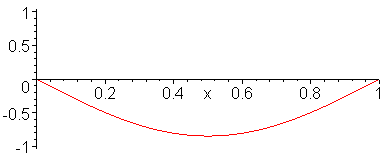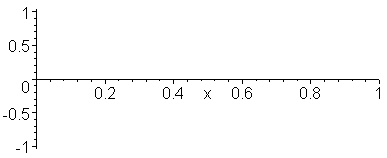
Different Modes of Oscillation (different wave frequencies). Again notice that the nodes are stationary. The crests peaks of the combined waves are Antinodes. |
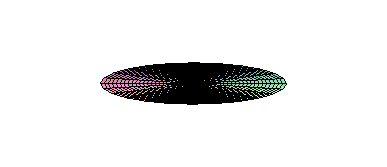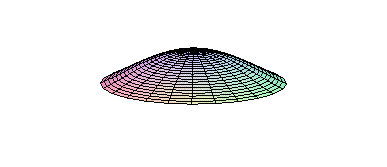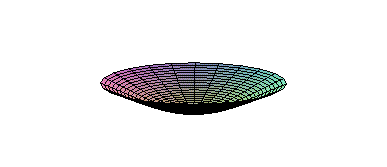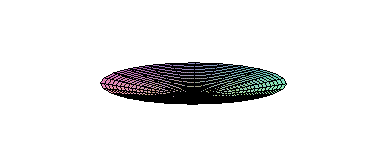
Modes of Oscillation (different wave frequencies) on a drumhead. There are now stationary lines where the wave amplitude is zero . |
|
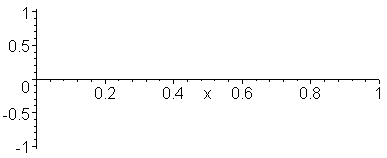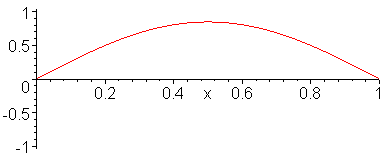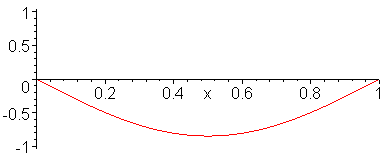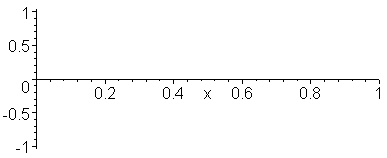
|
|
 |
In wind instruments, the waves are supported by the air in the tube; the wave speed is
The wave speed is then simply determined by the temperature of the air. This is an issue because this means that the pitch depends fairly strongly on the temperature in the room. The wavelength of the mode is again set by the length of the pipe, and so the frequency (pitch) of the mode depends mainly on the length of the pipe. The harmonic content is determine by the boundary conditions on the pipe and so the quality is affected by whether the pipe is open or closed. |