Due: end of Dec 5, 2022, Write-up example
Local noon is when the Sun reaches its highest point in the sky above the horizon. Local noon, in general, not the same time as clock noon. In this exercise you will determine the time of local noon in Eugene for a given date. To do so:
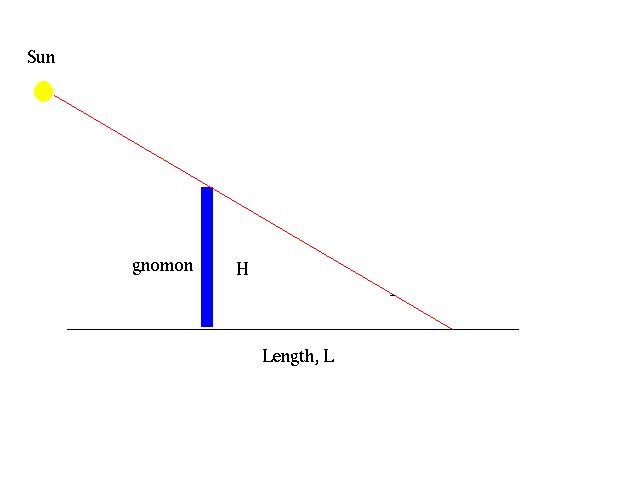
1. find a flat spot and place a stick (pole) into the ground. Make sure that the stick stands vertically. The vertical stick is referred to as a gnomon (see below). We will measure the length of the shadow cast by the gnomon as various times to accomplish our goal.

Date:
Location (city is good enough):
Gnomon Height, H:
Between the times say, 11 am and 3 pm, measure the length of the shadow cast by the gnomon. Record your measurements in the table below:
|
|
|
|
2. Plot your data on the graph below:
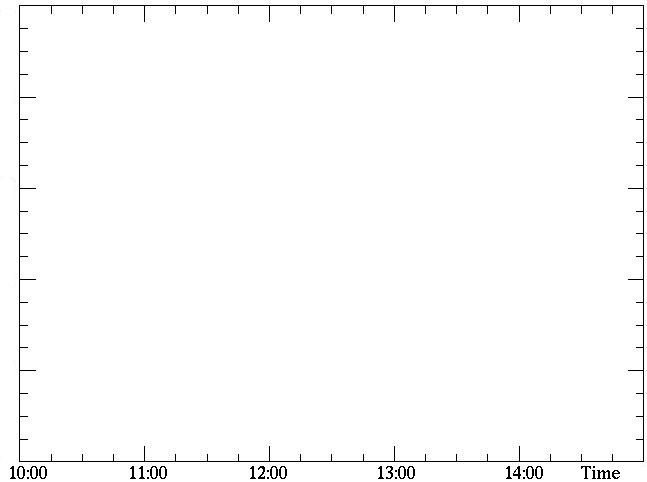
At what time is local noon? ________ Does local noon lead or lag clock noon at this time of year? ________
3. What is the maximum altitude above the horizon reached by the Sun (on the day you performed your observations)? ________ Use the table below to estimate your answer. (For a more precise result note that the Altitude A = tan-1 (H/L), that is, the altitude is the inverse tangent of the ratio (H/L).) The longer the shadow (the smaller the H/L), the lower the altitude of the Sun.
|
|
|
4. In which direction (NSEW) does the shadow cast by the Sun point at local noon? How does this direction compare to the direction as determined by a compass?