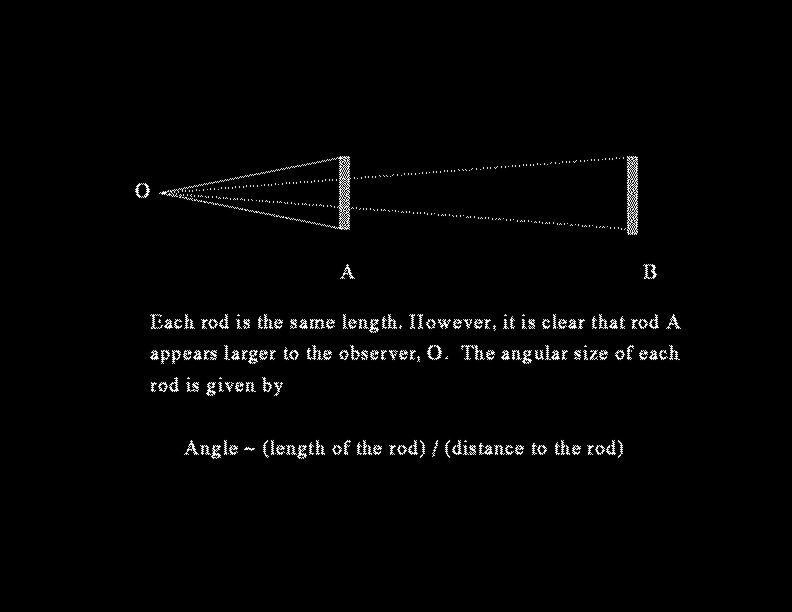
Before moving on, I need to make some remarks about how astronomers measure angles. The size of the angle subtended by an object depends upon how far away the object is from us. The greater the distance, the smaller is the angle (e.g., railroad tracks converge in the distance).

For most astronomical measurements, the angle is proportional to s/D, where s is the size of the object and D is the distance to the object. The proportionality constant depends upon the units used to measure the angle. The most familiar unit for angles is the degree. There are 360 degrees in a circle. A more natural unit is what is known as a Radian. There are 2 pi Radians = 6.28 Radians in one circle.

Why are Radians natural units?

The angular size can be found from

angle = 57.3 (s/D) degrees

Under most astronomical conditions, angles are very small, much smaller than 1 degree. Because of this, different measures for angles are used.

The idea is similar to what we do for time. We have many units for time --1 year = 365 days; 1 day = 24 hours; 1 hour = 60 minutes; 1 minute = 60 seconds. We choose the most convenient unit depending upon the situation. It is silly to talk about how old you are in seconds; you use years. By the same token you do not talk about how long this class in terms of centuries; you use minutes or hours. You usually try to choose the units to match the size of the thing you are measuring.

For angles, because most astrophysical angles are tiny, smaller units for angles are used;

• 1 degree = 60 arc minutes
• 1 arc minte = 60 arc seconds

The typical astronomical angle is on the order of arc seconds (i.e., 1/3600 of a degree!!!). This is an impressively small number. The average human being can resolve an angle on the order of one arc minute.

Comment--what does resolution mean? Well, return to the railraod track. We know that up close the rails on a railroad track are parallel. However, as the track moves off into the distance, the rails appear to get closer and closer together and that somewhere near the horizon we cannot make out that there are two tracks; we can only see (resolve) one track. What resolution measures is the smallest angle that we can see with our eyes.

So, what is Annual Trigonometric Parallax?

Now, what effect does the Earth's motion produce or more precisely, how large are typical parallax angles (that is, how large are the typical annual shifts in the positions of stars)? The astronomical unit is around 93,000,000 miles or 1.5 x 10⁸ kilometers. Outside of the Sun, the closest star to the Earth, Proxima Centauri, is at a distance of 10¹⁴ kilometers (4.3 light years). The parallax angle is then

P = 57.3^o (1.5x10⁸km/10¹⁴km) ~ 0.0001^o

which is ~ 1/3 of one arc second which is << than the resolving power of the human eye.

Because of the astronomical distances to even the closest stars, parallax is not detectable with the unaided human eye.