
A series of concentric circular waves moves away from the disturbance. |
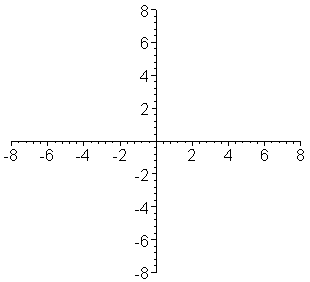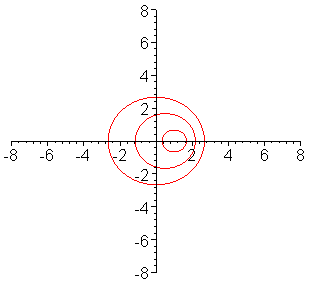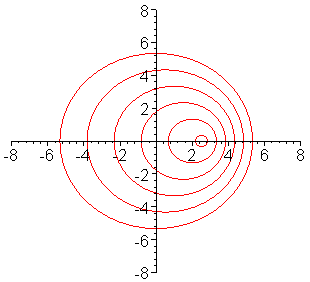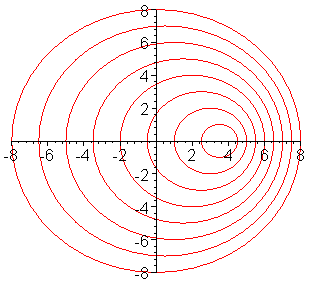
Circular waves are still produced but the distances between the crests of the waves depends upon where you sit. |
Doppler shifts are part of the phenomenology of waves (here, we treat the light we receive from stars as a wave-like phenomenon). To understand why this is important for planet detection, let us look at the analogous classical Doppler phenomenon. First, consider what happens to a pan full of water if I drop a rock into it (or disturb it in any manner). I would generate a pulse that moves out from the point of disturbance in all directions.
Next, suppose I move the point at which I tap the water. For example, suppose I start tapping the water at the center of the pan but for each successive tap, I move a short distance to the right. This is the case shown to the right.

A series of concentric circular waves moves away from the disturbance. |
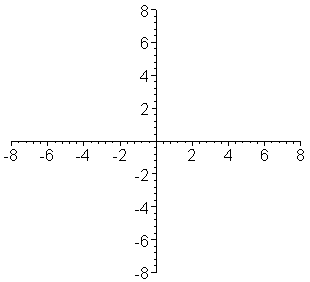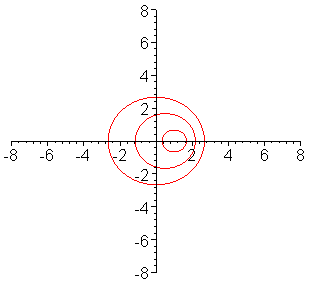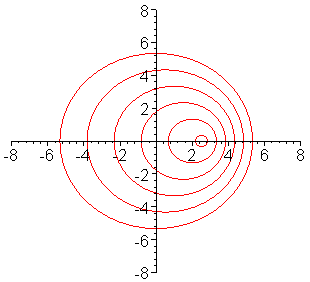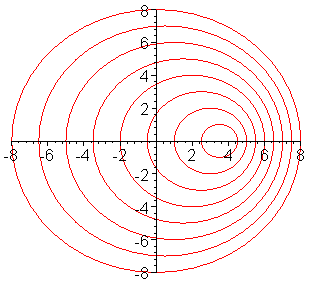
Circular waves are still produced but the distances between the crests of the waves depends upon where you sit. |
For the picture on the left, it doesn't matter where I sit while I watch the wave. Whether I sit on the right, on the left, at the top, or at the bottom, the rate and distance between the passing crests is the same, I see the same wavelength for the wave wherever I sit.
Q: What if I sat on the right hand side of the picture on the right, how would the wavelength I measure compare to the wavelength that I would measure if I sat on the left side of the picture?
Q: How does the size of the Doppler shift depend on the speed that the source is moving?
