Radiometric Age Dating Radioactive elements provide accurate clocks. If one can measure the relative abundances of a radioactive element (parent) and its decay product (daugher), the age of the rock may be inferred based on its half-life. The half-life of an element is the time it takes for one-half of the parent to decay to the daughter. See the plot to the right. Some useful radioactive decays are Uranium 238 to Lead 206 + heliums + electrons, t1/2 = 4.5 By Uranium 235 to Lead 207 + heliums + electrons, t1/2 = 713 My Thorium 232 to Lead 208 + heliums + electrons, t1/2 = 13.9 By Plutonium 241 to Bismuth 209 + heliums + electrons, t1/2 = 2.4 My Potassium 40 to Argon 40 + positron + neutrino, t1/2 = 1.3 By Rubidium 87 to Strontium 87 + electron + anti-neutrino, t1/2 = 47 By

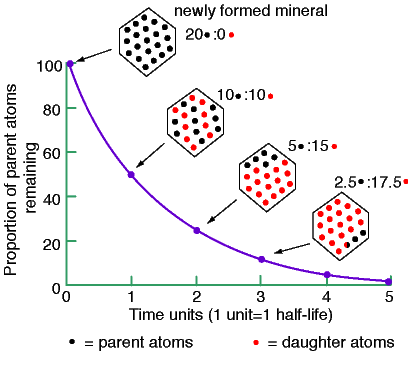
At birth, the rock has 20 parent atoms and zero daughter atoms. (1) After 1 half-life, half of the parents decay to 10 daughters; (2) After another half-life, half of the remaining parents decay to daughter atoms, that is, 5 atoms decay. At this point, we have 5 parents left and 15 daughters. (3) The decays continue until no parents are left to decay. Using the ratio of parent to daughter atoms allows us to determine the age of the rock. (a) If we have equal numbers of parent and daughter atoms, the rock is 1 half-life old. (b) If the ratio of the number of parents to daughters is one-third, the rock is 2 half-lives old. (c) If the raio of the number of parents to daughters is one-seventh, the rock is 3 half-lives old. (d) The age can be estimated until all of the parent atoms decay.