ARE WE UNIQUE?

A good resource on extra-Solar System solar systems

The current belief is that the process of Solar System formation is one of many natural outcomes of star formation. That is, it is simply one way in which the collapse of a rotating ISM cloud may turn out. Other outcomes are the formation of binary star systems (or other multiple star system)-- cases where the components have masses more in line with each other. This notion is supported by the fact that over 50 % (perhaps up to 80 %) of all stars are contained in multiple star systems. Given this motivation and the simple desire to know if we are unique has pushed many people to look for other solar systems in our Galaxy.

The types of searches can be broken down into direct planetary searches and indirect planetary searches.

• Indirect searches are based on the fact that the objects in a solar system do not orbit about the star, but rather orbit about the center-of-mass of the system. This means that the star also moves which may be detectable.

• Direct planetary searches look for eclipses of stars due to the motions of the planets (although this is very difficult) and searches are geared to locating other Solar Nebulae.

Here, we consider the following strategies:

• astrometric searches (ID)
• spectroscopic searches (ID)
• pulsar-type searches (ID)
• occultation searches (D)
• solar nebulae searches (D)

Before we go into each method in more detail (and discuss the successes of each method), let me state that there are only two unambiguous results; one due to the pulsar-type search technique and the other due to the spectroscopic search technique.

INDIRECT SEARCHES

In orbital systems, the bodies move around the center-of-mass of the system. The center-of-mass of a system is located a distance D from object 1 (mass = M) and a distance d from object 2 (mass = m). The relationship between

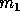
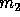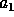
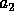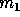
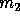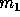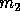That is, if then . In extra-solar systems, we will always have , where is the mass of the star and is the mass of the planet and so 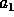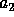and the motion of the star will be very small. In our Solar System, the dynamics are dominated by the Sun and Jupiter and so,

and

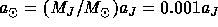
The distance of the Sun from the Solar System center-of-mass is therefore around 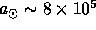kilometers

The radius of the Sun is around 7 x 10 kilometers and the Sun orbits about a point a little bit outside of its radius. The orbital period is roughly 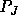= 11.9 years ( Why?) so that the orbital speed is roughly 13 meters per second, the speed of a running human (albeit a fast one).

Indirect planetary searches look for the small changes in the position of the star ( astrometric searches) and for effects due to the fact that the star is undergoing a slow orbital motion ( spectroscopic searches and pulsar-type searches).

1. Astrometric Searches

To get a feel for the difficulty of astrometric searches, suppose that we lived on the nearest star to the Earth (excluding the Sun), Proxima Centauri. Could we see our Solar System? Proxima Centauri is a distance of 4.3 light years = 1.3 parsecs = 4.2 x 10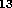 kilometers from the Earth. This is a long way away -- 1 Astronomical Unit = 1.5 x 10 kilometers!!!

Jupiter orbits around the Sun in an orbit of size 5.2 A. U. with a period of 11.9 years. The size of the Sun's orbit is 8 x 10 kilometers. From Proxima Centauri this would correspond to an angular size of angle = 8 x 10 km / 4 x 10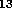 km = 2 x 10 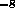Radians = 0.004 arc seconds

Given current technology for ground-based observatories, this is right near the limit of what is do-able. It is possible that Jupiter-sized planets may be detected in this manner for the nearest stars.

Note that astrometric searches are sensitive to how close the stars are to the Earth. The technique only works for nearby stars. The farther away the star, the smaller the angular size of its orbit.

There are currently no good candidates. The most famous one is Barnard's star, however, the results are ambiguous and seemingly not repoducible. In the future, we will develop space-based experiments which will have pointing accuracies of better than 0.00001 arc seconds and will thus be able to see nearby planetary systems if they xbmst. The limits of the search are 30 light years to detect planets > 10 times the mass of the Earth. There are roughly 1,000 suitable stars in this neighborhood of the Earth.

2. Spectroscopic Searches

Spectroscopic searches try to detect evidence of the motion of the star. In order to understand what is done, we need to discuss the phenomenon of Doppler Shifts

Doppler shifts are part of the phenomenology of waves (here, we treat the light we receive from stars as a wave-like phenomenon). To understand the Doppler phenomenon, consider what happens to a pan-full of water if I drop a rock into it (or, in fact, disturb it in any manner).

I define the wavelength of this phenomenon as the distance between the wave-crests.

Now, let us consider a slightly different physical situation. I apply periodic disturbances (that is, I still tap the water every second), but instead of tapping the water at the same spot (e.g., at the center of the pan), I move the point at which I tap the water. For example, I start tapping the water at the center of the pan but for each successive tap, I move a short distance out from the center.

Schematically,

Depending upon where I sit, the wavelength of the disturbance will either be smaller or larger than for the nonmoving case.

The size of the contraction or stretching depends upon how fast the object moves

The results can be stated more precisely by noting that if I sit on the side of the tank where the point of distrubance is approaching, the wavelength is shorter. If I sit on the side of the tank where the point of disturbance moves away from me, then the wavelength is larger. It is direction of motion which is the key. In fact, if I sit on the side of the tank, then the wavelengths will be the same as for the stationary case (I cannot a stretching or contraction of the wavelength).

The preceding phenononom is the Classical Doppler Effect. An analogous effect occurs for the light produced by a star. In this case, the size of the effect (the amount of stretching or contraction) is given by

Here 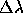is the how much the wavelength of the light is changed by the motion, 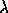is the wavelength of the light, c is the speed with which light travels given by c = 300,000 kilometers per second and v is the orbital speed of the star.

So, how large of an effect is this expected to be? Again, use our Solar System as a typical system. The size of the orbit of the Sun is 8 x 10 kilometers and the orbital period is 11.9 years. Therefore, the orbital speed of the Sun is v = 2(8x10 meters)/(11.9 years x 3.1 x 10 seconds per year)

The orbital speed of the Sun is on the order of 14 meters per second. To observe this effect, we need to be able to observe something like a fast person running in the extra-solar system. The rather amazing thing is that with current technology this is possible! (The shift due to the orbital motion leads to a change in the wavelength of 4 x 10 .)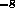

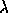Note that spectroscopic searches are fairly insensitive to how far away are the stars. All you need to do is to detect the shift in the wavelength of the light. This is independent of the distance. The only requirement is that you be able to "see" the star. This allows you to use the spectroscopic method even for very distant stars.

A recent exciting discovery concerns planets around 51 Pegasus.

There are at least two other systems people are following up on: 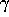-Cephei and HD1145762. These systems contain solar mass stars, and possibly contain objects on the order of Jupiter. However in the latter system, the orbit has a radius of 0.4 A. U. and given what we know about solar system formation, this does not seem likely (but recall 51 Peg). The former case has an orbit of around 2 A. U., which again is a little small for comfort. In the future there are large diameter (7-10 meters) earth-based telescopes coming on line which will pursue this problem. The large telescopes will allow

much higher accuracy to be attained and thus allow much more sensitive searches to be carried out.

3. Pulsar-Type Searches

There are objects in the Universe known as pulsars. Pulsars are actually a manifestation of the exotic stars known as neutron stars. neutron stars are interesting beasts in that they are roughly the mass of the Sun and therefore composed of 10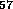 or so neutrons (and a few protons and electrons). The amazing thing is that they are roughly the size of Eugene (i.e., they have diameters on the order of 20 - 30 kilometers). This means that they have huge densities. Their densities are in fact roughly the same as that of the nuclei of atoms and so, in a sense, neutron stars are simply huge nuclei held together by gravity.

An interesting property of neutron stars is that they have intense magnetic fields and that many of them rotate very quickly. The fastest spinning ones in fact spin around over 600 times a second!! This behavior manifests itself in an interesting way. The magnetic field leads to the formation of hotspots on the surface of the neutron star which are carried into and out of the line-of-sight to an observer by the rotation. This causes the light from such stars to vary periodically. Such neutron stars are referred to as pulsars. The important thing about pulsars is that their pulsation periods are rock-solid stable and that over time scales longer than a year, they can be much more stable than the best Terrestrial clocks. In fact, it is the accuracy of the Terrestrial clocks which holds them back. The extremely high accuracy of the pulsing allows very sensitive tests for orbital motion to be made. This sensitivity is utilized when people search for planets around pulsars.

Pulsars are used to search for planets in a manner analogous to the spectroscopic method. In fact, I could use the same pictures to demonstrate the technique. To understand this, simply replace the omnipotent observer who disturbed the water with a pulsing neutron star. The time between the pulses will depend upon whether the neutron star approaches or recedes from the observer. The change in arrival time is again dependent upon the speed of the motion of the neutron star 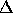period/period = v / c

Again, for a star like Proxima Centauri, the change in the period is 4 x 10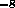 of the period. That is, we must be able to measure the period of the pulsar to better than an accuracy of 1 ten-billionth of a second if the pulsar period is a few milliseconds. This is amazing and yet quite possible. The fastest pulsar has a period of around 1.56 milliseconds and we know the period to an accuracy of better than 10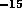 period!!! Using the pulsar search technique we can detect planets as small as the Earth. This is a huge improvement (the Earth is only 0.003 the mass of Jupiter).

The pulsar method is also independent of the distance to the star. It only demands that you measure the differences in the arrival times of the pulses.

PSR 1257+20, a millisecond pulsar system, has been reported to harbor three planets. The planets have orbital periods of 67 d, 98 d, and 25 d and planetary masses on the order of the mass of the Earth. These are thus reasonable parameters given what we understand about solar system formation. However, the catch is that the star in this system is a neutron star, an exotic star which is the remnant of some past catastrophic event. It is believed that most neutron stars were formed in supernova explosions. In any event, neutron stars are not normal stars. The key point of the discovery of planets around a neutron star is that planets can form in even the most extreme environments and therefore it is likely that the planetary formation process is not improbable and thus there are most likely many planetary systems in the Universe.

DIRECT SEARCHES

The obvious problem with direct detections of planets is that stars are very bright and planets are very faint. This means that it is very difficult to see planets in the glare of the stars. Further, because planets are small,

eclipses of stars by planets are not likely to lead to large changes in the light output. This, again, makes direct detections of planets difficult.

• There are no direct detections of planetary system searches which are underway and have reported results.
• There are reports, however, of pre-solar system objects (protoplanetary disks). Examples are,

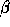  • Pictoris. These are large, 100 A. U. dust disks which may be the first stages in solar system formation (or perhaps star formation).

  • Proplyds in the Orion Nebula

Non-Solar Mass Stars?

Most estimates made above were based upon stars the same mass as the Sun. Suppose that the star had a different mass, how would things change? Why should things change?

Mass Dependence

Consider two cases. Oh, still use a star at the distance of Proxima Centauri and a Jupiter-sized planet in the estimates.

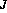• Consider a planet in an orbit with period P = 11.9 years
• Consider a planet which forms where ice can first become solid

Constant 11.9 year Orbital Period

Recall that Kepler's 3rd Law is P = a / M. So, if we take a constant orbital period of 11.9 years, then we see that for more massive stars, the size of the orbit must be larger. ( Explain why this is true).

Orbital Properties

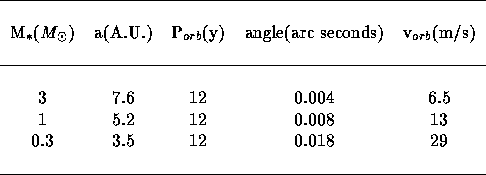
Hmmm. Why is the angular shift smaller for the more massive stars? After all, the total size of the orbit is larger. Anyway, we see that for the lower mass stars, it is easier to see planets for both the spectroscopic and astrometric methods.

Ice Solidification Criterion

If we assume that the planet forms where ice can first solidify (T - 150 F) then we can infer the structure of the solar system. We can argue that more massive stars should be hotter (and thus brighter). So, the radius where ice can solidify is larger for more massive stars. Based on these types of ideas, we find the following table.

Orbital Properties

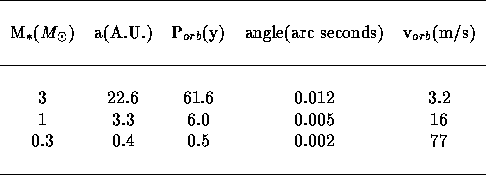
We see that for the lower mass stars, it is easier to see planets using the spectroscopic method but that for higher mass stars, it is easier to use the astrometric method. However, none of the cases shown is easy. It will take quite an effort to detect other planetary systems.