Earliest models were built by the Greeks. They were Earth-centered, or geo-centric. Note that what this means is they attached physical meaning to the Celstial Sphere construction. They not only used the notion that the Earth was sitting in the center of a large sphere, but they thought that this was how the Universe worked. They had reasons for believing this idea, e.g., lack of parallax and some conclusions based on faulty physics. The Greeks were not completely arbitrary.
The geo-centric models reached their pinnacle in the work of Ptolemy (~ 140 A.D.), who described his model in the Almagest. The model worked well enough in that the observational data was not accurate enough to show that the model was wrong!!
Copernicus (1473-1543) championed the idea of a Sun-centered helio-centric Universe. He published his work on his deathbed in the book, de Revolutionibus Orbium Celestium. The model was not immediately embraced for various reasons, some of the best were that it did not work any better than the geo-centric model and it had no foundation in physics. (For much the same reasons, the similar model proposed by Aristarchus of Samos [310-230 B.C] was rejected by the Greeks).
The assumptions of the Copernican model are:
2. All orbital motions are circular
3. Sun-centered; all planets orbit about the Sun.
2. the correct explanation for retrograde motion
3. the cause for the variable brightnesses of the planets
4. the phases of the planets
5. ....
A nice thing that Copernicus did was to deduce the scale of the Solar System. He did not figure out how big the Solar System was in kilometers, but he did figure out the relative size based on the size of the orbit of the Earth (i.e., on the Astronomical Unit). See Figures.
Results are amazingly good. However, despite the nice features of the helio-centric model, it was not accepted. Better data so that more compelling arguments could be made were needed.
The first great optical observer. His primary contribution to astrophysics was the precise data he collected on the motions of the celestial bodies. His data were accurate to within 1/60 of one degree, i.e., to within 1 arc minute. The data were accurate enough to allow people to rule out theories of the motions of the celestial bodies. The result of his (and other people's) studies was to show that neither the Ptolemaic nor the Copernican models were acceptable. Both models were not consistent with the data!!!
Comment--A simple thing which Tycho did which greatly improved his accuracy was to make several measurments of quantities and to then average his results in order to arrive at his final answer. This is standard practice today, but was highly unusual during Tycho's time.
Kepler worked with Tycho and with Tycho's data (after the death of Tycho). He developed the first accurate model for the motions of the planets, Kepler's Laws of Planetary Motion. As we will discuss later, Kepler's laws are based on Newtonian physics and are, in fact, easily generalized so that, in suitable form, Kepler's laws apply to any system of objects bound together by their mutual gravitational attraction. For example, Kepler's laws apply to binary star systems, to the orbit of the Moon about the Earth, to the orbits of the moons of Jupiter about Jupiter, ... .
The most radical thing that Kepler did was to remove the assumption of circular motions, a motion viewed by the Greeks and Copernicus as sacred. This simple generalization allowed Kepler to make a model which was consistent with the data acquired by Tycho.
Law III: Harmonic Law
(years) = a
(A.U.).
)/(1+e
cos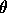
)
]]
.
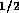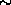1/2 D x d so that
D'
d' = D
d
v'
time = D
v
time
v' = D
v
v' / v = D / D'
v(perihelion)/v(aphelion) = (1+e)/(1-e)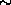 
1 + 2e
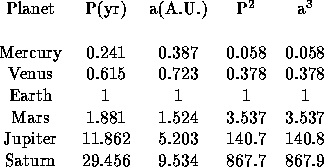
Note that the last two entries in the above table are odd.
It's clear that the orbital periods are shorter for the inner planets, but is it also true that the orbital speeds are larger for the inner planets? How does the orbital speed depend on a?
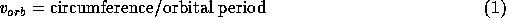
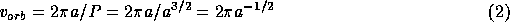
20 miles per second.
What is the orbital speed for Saturn?
In the early 1600's Galileo Galilei (1564-1642) made extensive observations with one of the first astronomical telescopes. He discovered several significant things: (1) the phases of Venus; (2) blemishes in the heavens {sunspots, lunar craters, lunar maria ("seas"); (3) Saturn had "ears"; (4) the four large satellites of Jupiter (the Galilean satellites); (5) ... .
All of these discoveries were interesting in their own right, but here we consider the Galilean moons (Io, Europa, Ganymede, and Callisto) because of what they show about Kepler's Laws of Planetary Motion.
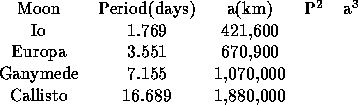
We could calculate P
and a
using the above numbers, however
things would not be obvious. Let's scale the results just as we
did for the Solar System. For the Solar System, we chose to use the
Earth as our preferred object. That is, we chose to measure the
P's and a's in terms of the Earth's period and orbital size. Let's do
something similar for the Galilean moons. We will measure
everything in terms of Io. To do so, we simply divide all periods
by the period for Io, P = 1.769 days and we divide all orbital sizes by
the orbital size for Io, a = 421,600 km. This leads to
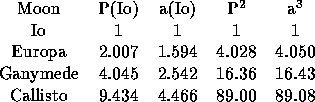
As advertised, the Galilean moons obey Kepler's Laws of Planetary Motion. They, in this sense, form a mini-Solar System. As we will argue later, the Galilean moons also mimic the Solar System in terms of the compositions of the moonns.
This suggests that Solar System formation is a natural process
Titius-Bode Law. A simple mnemonic for remembering the sizes of the orbits of the planets is given by,
a = (3 N + 4 ) / 10 Astronomical Units
where we set N = 0, 1, 2, 4, 8, 16, 32, and so on. For Mercury, N = 0 and so a = (0 + 4 ) / 10 A. U. = 0.4 A.U. Pretty close to the correct answer. For Venus, N = 1 and so a = 0.7 A. U., hmmmm. For Jupiter, N = 16 and so a = 5.2 A.U. The law works well for some planets. Further, an interesting prediction was made when the law was proposed. There was no planet for N = 8, i.e. for a = 2.8 A.U. However, subsequent work showed that there was a belt of small rocky objects near a = 2.8 A.U. (the asteroid belt). This is probably the planet predicted by the Titius-Bode relation.
Astronomers used to ignore the Titius-Bode relation as only an interesting quirk of numerics. However, although there is (as of today) no physical explanation for the law, there is probably physical content in the law. My guess is that the Titius-Bode relation contains information on the stability properties of the orbital arrangement of the planets.
Newton developed the physical theory which led to an understanding of Kepler's Laws. Galileo began the studies which culminated in Newton's work, however, here I concentrate on Newton because he tied things together and essentially started a new science, Physics. Newton published his work on mechanics and optics in the book, Philosophiae Naturalis Principia Mathematica
on the urging of his friend, Edmund Hillary. In the Principia, Newton states his three laws of motion:
This is in contrast to Aristotilean (Greek) physics where the natural state of a body was at rest (this notion was based on the observation that friction eventually brings everything to rest).
A modern re-statement of Newton's first law is known as the
Conservation of Linear Momentum
What is linear momentum?
Schematically, we have that
change in momentum 
applied force
This is then re-phrased as
change in momentum = change in ( mass x velocity )
Since Newton assumed that the mass does not change, we have that
change in momentum = mass x change in velocity
Newton defined the change in the velocity as acceleration. Given these definitions, Newton's second law is concisely stated in the more familiar form,
Force = mass x acceleration
F = m a
Comments:
1. The second law gives us a way to define what mass measures. Mass measures the inertia, the resistance to a change in the state-of-motion of an object. A massive object is harder to accelerate (move) than a less massive object. It is easier to push a mosquito than to push an elephant. We define
Mass (inertial) = Force / acceleration
2. What about motion in a circular orbit?
3. F = m a. Hmmmmm. Let us re-write this as F = m (change in velocity) / (time interval) = change in momentum / time interval. So, if there is no applied force, then the change in momentum is 0 and the linear momentum of the object is constant. So, in this sense, Newton's second law of motion also contains the information present as Law I.
This law is also a consequence of the conservation of linear momentum and can be re-stated as, the total momentum of a system is constant in time unless the system is acted upon by some outside force.
Examples:
1. Hitting a baseball
2. moving around on ice
3. astronaut in space
4. rocket
Let's reconsider the moving around ice example in more detail. At time = 0, a person stands holding a rock on a frozen pond. Because no one is in motion, neither the rock nor the person has any momentum. The initial state of affairs is then
.
The person and the rock comprise the system. Now suppose the person throws the rock in a direction horizontal to the ground. What happens? Well, the rock goes in one direction and the person moves off in the opposite direction. Note that since the person and the rock form a system and no outside force was applied to the system (nothing outside of the system applied a force to the system, that is) nothing happened to change the total momentum of the system. We must then still have
because of the Conservation of Linear Momentum. That is, p
=
- p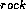
and so we have that the change in momentum is
If the push applied to the rock took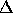 
t seconds, we re-write this
expression as
Now, using the definition of force from Law II:
Ah ha, the person felt a force, equal but opposite to the force applied to the rock. So from our analysis of the ice mover problem in terms of momentum conservation, we see that Newton's third law is simply a re-statement of the notion of the Conservation of Linear Momentum.
In one form or another, all of Newton's laws have to do with the conservation of linear momentum. This should suggest that this conservation law is important. It is quite important and is one of the basic tenets of physics on all levels.
Interestingly, there have been experiments where it appeared that the conservation of linear momentum failed. In particular, an experiment in the middle part of this century which studied the decay of certain radioactive elements did not appear to conserve momentum. A nucleus which was initially at rest (i.e., the system had zero momentum) decayed and the momentum of the resultant particles were measured. Surprisingly, based on the momentum of the detected particles, linear momentum was not conserved!! Given this experiment, one could either conclude that conservation of momentum was violated or that some unknown "invisible" particle was produced which carried off the momentum. Because of the reverence with which conservation of momentum was (and is) held, the choice was to suggest that some undetectable particle carried off the momentum!! A particle was invented to preserve the law! In this way, the neutrino was predicted. It was eventually discovered later in the 1950's.