Daily Motions

DAILY MOTIONS


The daily (diurnal) motion of the celestial objects is caused by the rotation of the Earth on its axis. We see the stars rise in the east, set in the west, and then rise again in the east every 23 hours 56 minutes and 4.091 seconds (the sidereal day (in a sense, this is the time it takes for the Celestial Sphere to rotate once on its axis).



The stars appear to be fixed to the Celestial Sphere and since we are interested only in relative motion, we can imagine that the Earth is stationary and that the Celestial sphere is turning. The resultant motions are then rather simple. Because the stars do not move on the Celestial Sphere, they maintain constant distances from the rotation axis and so simply trace circles on the sky centered on the projection of the axis of rotation of the Earth onto the Celestial Sphere (that is, the North or South Celestial Pole).

These daily paths (the circles) are referred to as diurnal circles.

The daily motions of all celestial objects (the stars, the Sun, the Moon, and the planets) follow this pattern. Note that the objects move from east-to-west across the sky which means that the Earth spins from west-to-east. Or, as viewed from the NCP, the Earth rotates in the CCW-sense.



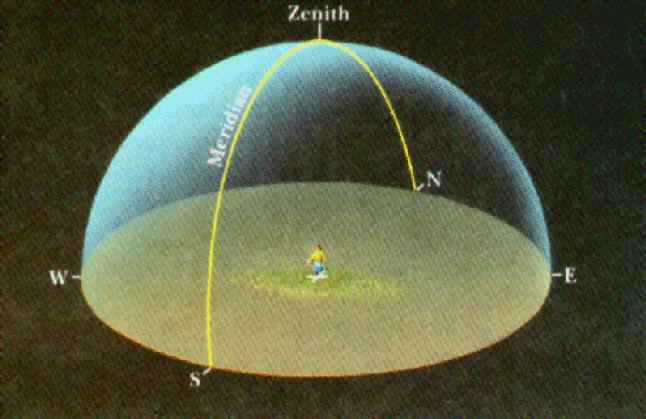
How does the appearance of the sky change as we move in latitude on the Earth?



To answer this question, we first define the horizon. Because we cannot look through the Earth, we can only see that part of the sky which is above the ground.

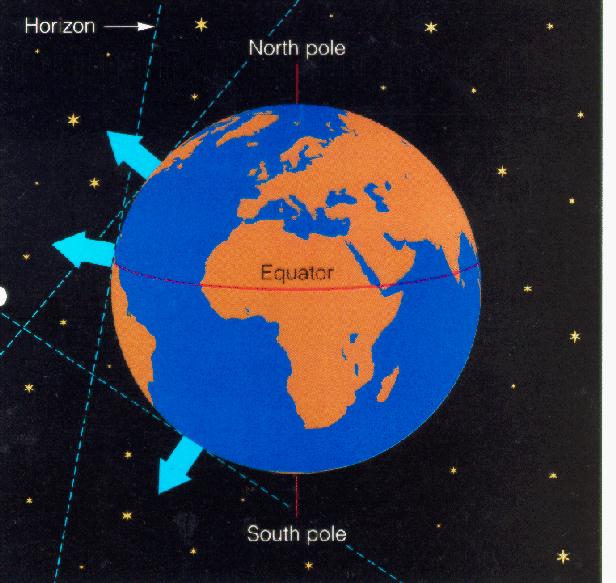
The point directly above the head of the observer is referred to as the zenith. The point directly below the feet of the observer is referred to as the nadir. The circle that passes through the north point on the horizon, the zenith, the south point on the horizon, and the nadir is referred to as the meridian. The horizon is 90 degrees down from the zenith. Note that every observer has his or her own zenith and horizon; it is a purely locally defined system. Everyone in this room has roughly the same zenith and horizon, but they are not precisely the same. The zenith and horizon for an observer changes as he or she moves (in latitude) on the surface of the Earth.

The Sky at Different Latitudes

North Pole (latitude=90 degrees):

    the zenith and the NCP coincide and the horizon coincides with the Celestial Equator. A general result which is easily shown is that

    the altitude of the NCP = the latitude of the observer and that the Celestial equator makes an angle of 90o - the latitude of the observer,

    consequently, all diurnal circles are parallel to the horizon. All visible stars don't rise or set; all stars are circumpolar. For a given latitude,

      whether a star is circumpolar is determined by how close it is to the NCP or SCP. Stars closer than the latitude of the observer to the pole are circumpolar.

Equator (latitude=0 degrees):

    the NCP sits on the North point of the horizon while the Celestial Equator passes through the east point on the horizon, the zenith and west point on the horizon. The diurnal circles are roughly perpendicular to the horizon near the east and west points on the horizon. All stars rise and set; no stars are circumpolar.


Intermediate Latitudes

    Note that the altitude of the NCP above the horizon is 90 degrees at the North Pole and 0 degrees at the equator. At intermediate latitudes, the diurnal circles are tilted with respect to the horizon. Stars that are within the latitude of the observer from the NCP never set. In Eugene, the NCP has altitude around 44o so that stars within 44o of the NCP are circumpolar in Eugene.

Today, Polaris, the North Star, sits right near the NCP. There is no comparable star near the SCP in the southern hemisphere.


Time: The Solar Day versus the Sidereal Day

The sidereal day is 23 h 56 m 4.091 s. The sidereal day is defined as the time it takes a star to make a complete trip around the sky. The Solar day is defined as the time it takes the Sun to make two successive crossings of the meridian:

If the Earth were stationary, then the Solar Day and the Sidereal Day would be precisely the same. However, we know that the Earth also revolves about the Sun. How does this affect the Solar Day?

Because the Earth roughly moves at a rate of (360 degrees)/(365.25 days) ~ 1 degree per day, the Earth will have moved 1 degree after 1 day. This means that in order for Sun to return to the Celestial Meridian, the Earth must turn roughly 1 more degree. That is, the Earth must turn ~1/365-th of the way around again to have the Sun reappear on the Meridian. This means that the Solar Day will be roughly 1/365-th times longer than the Sidereal Day.

If the Earth's orbital motion were steady with respect to the Celestial Equator, then this would be the entire story. Unfortunately, the Earth's orbital speed is not constant; it varies throughtout the course of the year because of the elliptical shape of its orbit and the mis-alignment of the ecliptic and the Celestial Equator. Consequently, the length of the Solar Day also varies throughout the course of the year. From a timekeeping standpoint, this is not acceptable and so the Mean Solar Day was defined to be the basis for timekeeping. The Mean Solar Day is the average length of the true Solar Day. The Mean Solar Day defines the clock day.

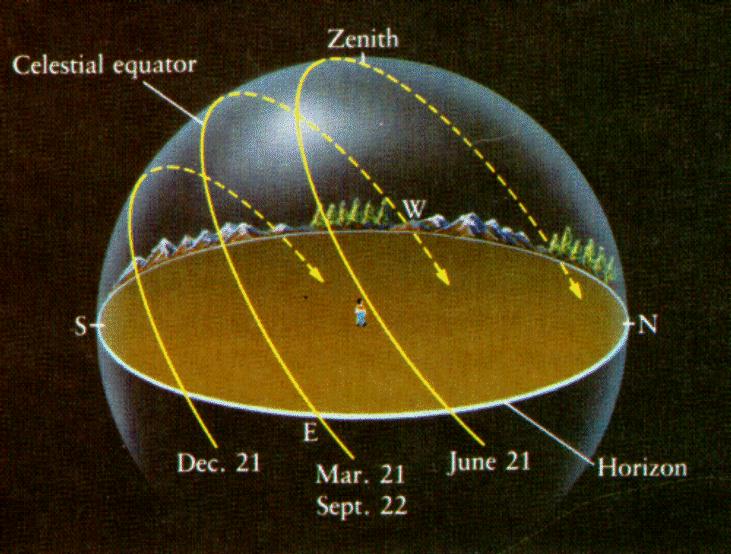
This is why the Sun sometimes appears to be late and sometimes appears to be early with respect to clock time. By early and late, I mean that the Sun does not cross the Meridian at the same time every day! This information is carried in the analemma (note the diurnal circles of Sun).