Hubble Law and Expansion of Universe II
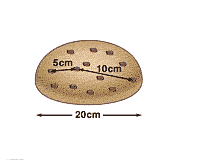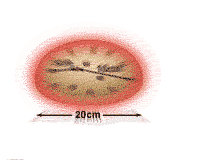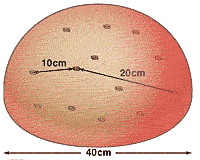
Imagine a very large universe in the form of an uncooked loaf of raisin bread.
Here, the universe could be very large but
fixed in shape with the raisins embedded in the loaf. Now cook the raisin
bread so that it doubles in size from 20 cm to 40 cm. As the raisin bread
doubles in size, the distance between every raisin also doubles in size.
That is, the raisin that was initially 5 cm away is now 10 cm away and the
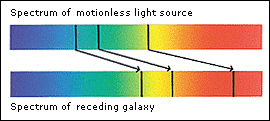
raisin that was 10 cm away is now 20 cm away. This means that if a wave
stretched between each of these raisins, the wavelength of each will have
doubled because of the expansion. Alternatively, it also means that it
would appear that the more distant
the raisin initially, the faster it would appear to move away from us!
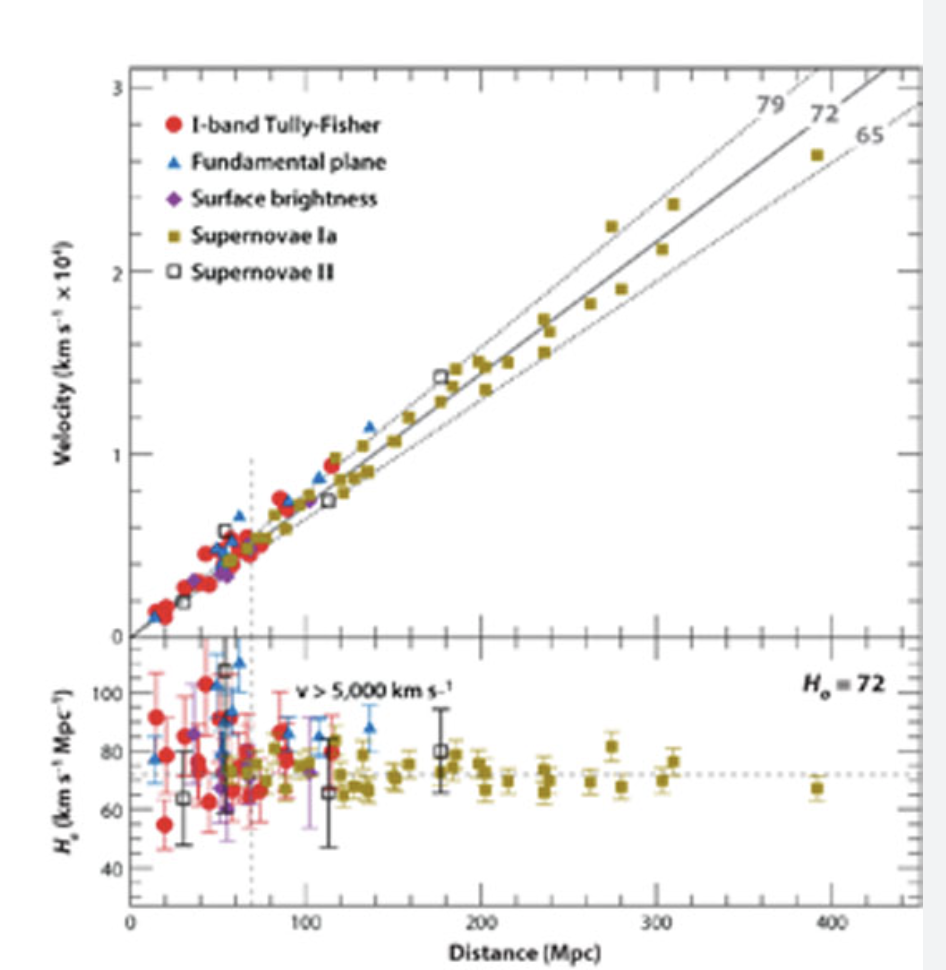
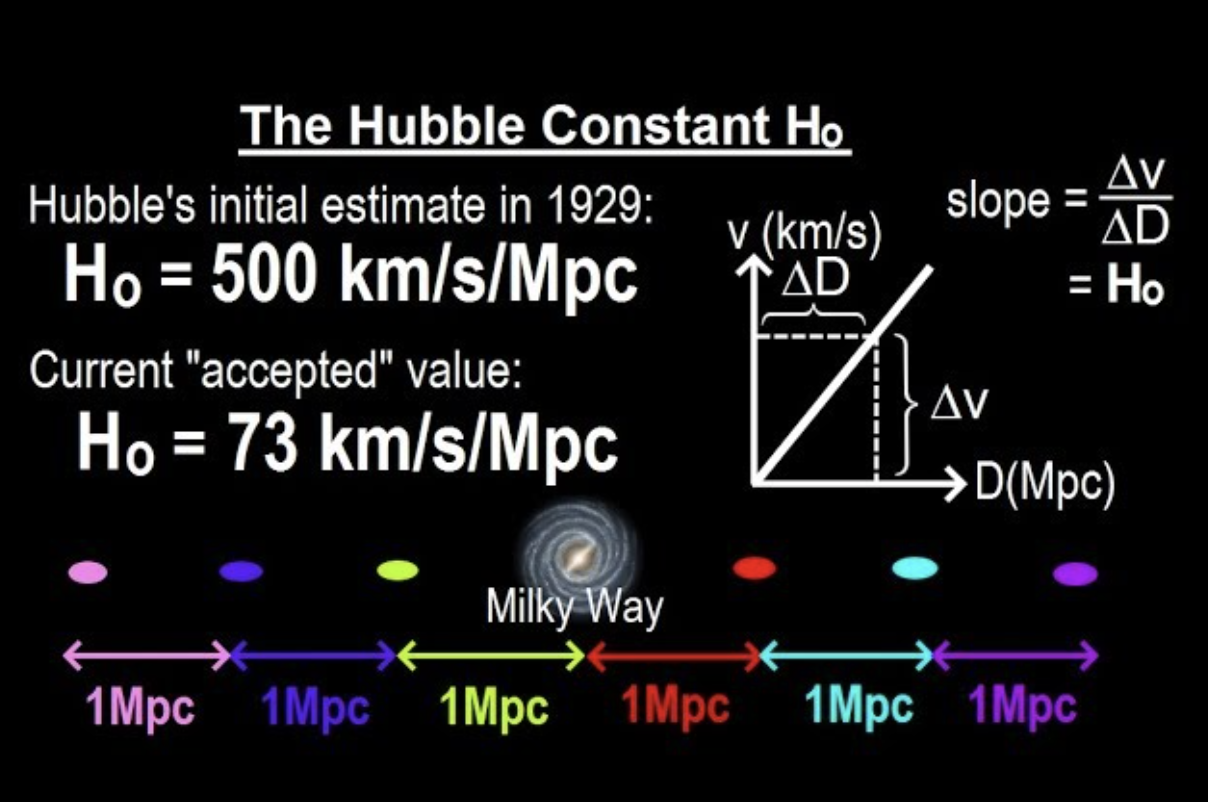
→ This again is Hubble's Law
Note that if the universe is sufficiently large and
we change our reference raisin, this same result would also hold,
that is, the new raisin would also observe Hubble's Law. In fact,
any arbitrary raisin
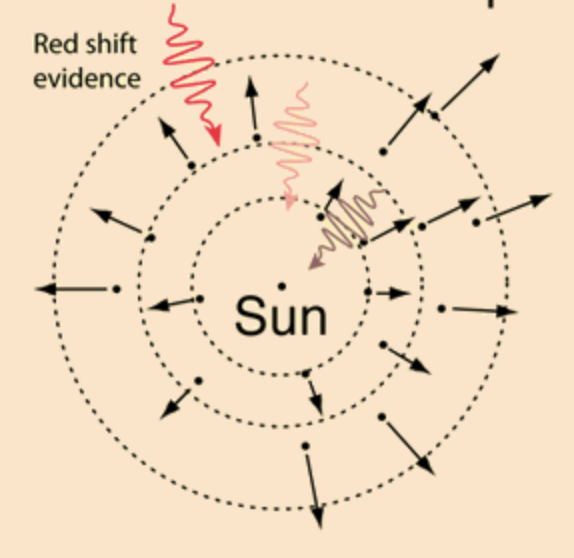
in the raisin bread universe would see every other galaxy
running away from them as well
thus making each look as if they were at the center of
an expanding universe, as long as the universe was sufficiently large.
|
 |