Mass of the Milky Way

Mass of the Milky Way Galaxy

The mass of an object is one of the most fundamental properties of the object. As such, reliable ways to measure mass are exceedingly important.

One way is to simply measure the optical emission (luminosity of a galaxy) and to (independently) determine the average mass of a star in the galaxy. This will then lead to an estimate for the mass of the galaxy if all of the luminosity is in fact due to the stars and all material radiates in a similar manner. This method has problems because it is sometimes difficult to know whether all mass produces radiation.

Another way to determine masses is to use our knowledge of physics (in particular, gravity). Since all mass is expected to interact gravitationally whether or not we can see it, we should be able to measure the mass of objects even if they are invisible to our eyes by their effects on nearby objects. This is the tact we now pursue.

Rotation Curves ===> Masses

Recall

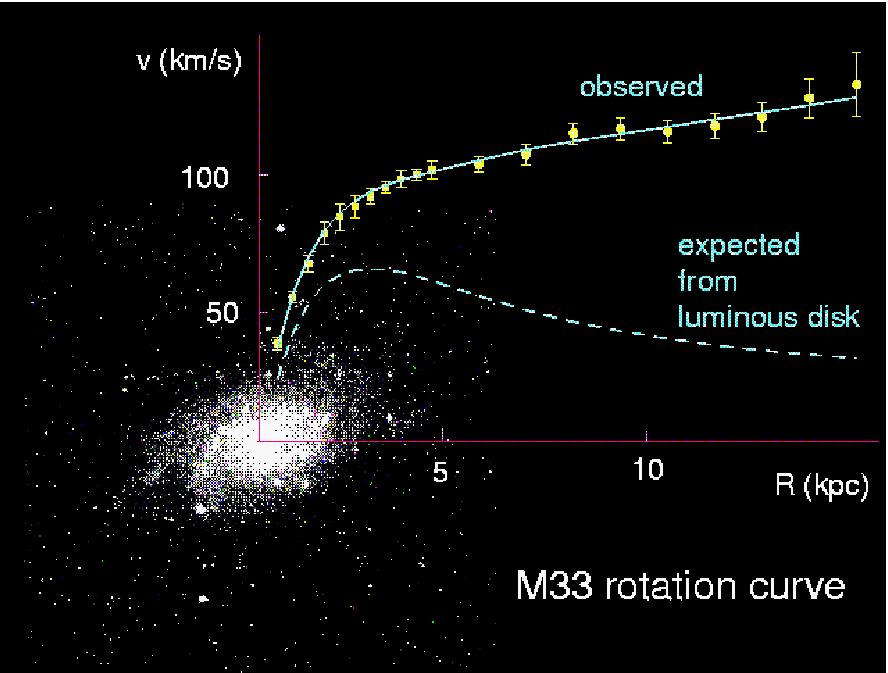
The gist of the method is to note that all objects are in orbit around the center of our Galaxy. To see how this allows us to infer the mass of our Galaxy, consider orbital motion. First, consider orbits about the Earth.

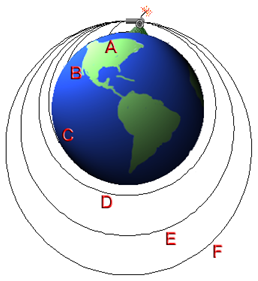A cannon fires a cannoball horizontal to the surface of the Earth. The Earth's gravity pulls the cannonball toward the center of the Earth.
If the cannonball has a small horizontal velocity, it is pulled to the ground before it has had much chance to move, Path A.
If the cannon shoots the cannonball at a higher speed, then it will travel further in the horizontal diretion before it is pulled to the ground, Paths B anc C.
Now, here is the key, because of the curvature of the Earth, the ground falls away from the cannonball. If the cannonball is given the correctvelocity, then the rate at which it falls and the rate at which the ground falls aways from it can be made the same and the cannonball never strkes the ground; it goes into orbit, Paths D, E, and F.
The critical speed required to go into orbit is determined by how hard the Earth pulls on the cannoball, F = - G(M_Em_ca)/R²

A similar situation arises for the Earth as it orbits the Sun.

The gravitational attraction between the Earth and the Sun tries to pull the two together.
The Earth overcomes this by orbiting around the Sun with just the right speed so that the centrifugal force just balances the attractive tug of gravity, ===> Gravity + Centrifugal Force = -GM_Sunm_E/d² +m_Ev_orb²/d = 0
The mass of the Sun and Earth and the distance between the Earth and Sun determine the strength of the gravitational attraction. The speed of the Earth's motion and the distance of the Earth from the Sun determine the strength of the centrifugal force. For a given size orbit, the mass of the Sun determines how fast the Earth must move to stay in orbit. To turn this around, note that if we can measure how fast the Earth moves in its orbit and the size of its orbit, then we can infer the mass of the Sun! The simple expression for the mass of the Sun is Mass of the Sun = M_Sun = v_orb²d/G where G is the gravitational constant, v_orb is the orbital speed, and d is approximately the distance from the Earth to the Sun.

This is the basis of the method used to determine the mass of the Milky Way galaxy (and other disk galaxies). However, before we move on, we have one further tweak to consider.

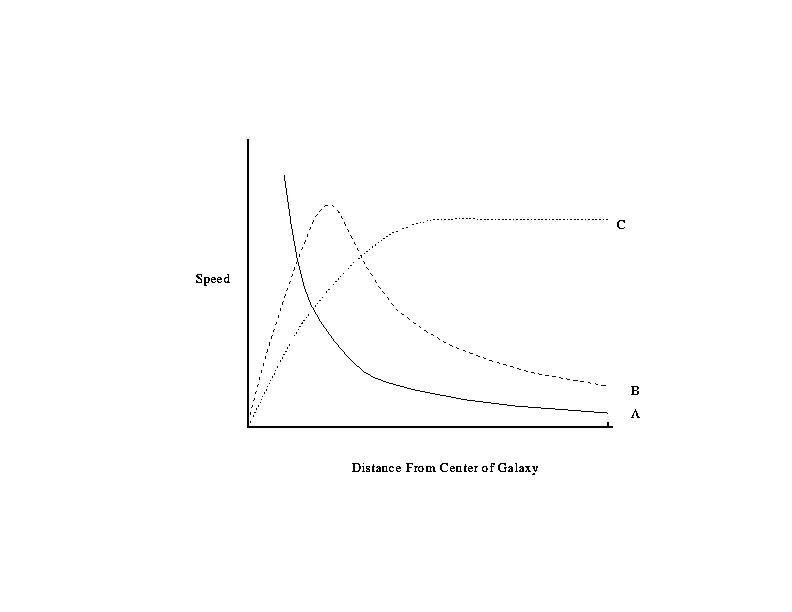
Orbits Outside the Body
In the Solar System, the planets orbit about the Sun. None of the planets orbit within the body of the Sun. The planets closer to the Sun feel stronger gravitational tugs due to the Sun and thus must travel faster to maintain their orbits. For example, the Earth travels with a speed of ~30 km per second. Pluto travels with a speed of ~4.6 km per second. This is typical of a sytem where bodies orbit outside of the attracting mass. This is shown by curve A.

Orbtis Inside the Body
Suppose we lived in a spherical system where the mass was spread out and we orbited inside of the body. Newton showed that only the mass contained within our radius contributed to the gravitational force on us. Note that although there is mass behind us and in front of us, the effect of gravity from these two sources cancel exactly!
So, as we approach the center of the object, the gravitational force we feel weakens and then vanishes. In such extended objects, orbital speeds do not fall-off as quickly (as in our Solar System) as one moves away from the center of the object. In fact, the orbital speed could stay the same and even possibly increase. These possibilities are shown by Curves B & C in the above figure.

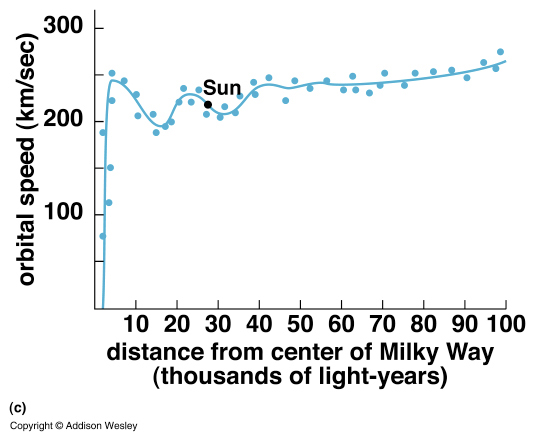
For the Milky Way, we find that the orbital speed increases and then remains roughly constant. This implies that we are still within the body of the Milky Way, even at the largest distances from the center of the Milky Way. We have not yet located the edge of the Milky Way; the Milky Way extends much further than the edge of the disk of stars (the visible disk)!

Recasting the equation given above (for the determination of the mass in a galaxy), we find
Mass = 9x10¹⁰(speed/220 km/s)²(orbit/25,000 ly) Solar masses

The mass contained in the Milky Way galaxy (in its visible disk) is then 2x10¹¹ Solar masses. Note that if we count up the visible stars to get the luminous mass, we find that we can only account for 30 % of the mass; 70 % of the mass in the visible disk of our Galaxy must be Dark Matter.

the mass contained in the Milky Way galaxy (out to as far as we can see HI gas) is 6x10¹¹ Solar masses.

Oh my, the mass where we can see stars is only 1/3 of the mass of the entire Galaxy of which only 30 % is normal luminous matter. This suggests that a lot of mass in the Milky Way is in some form which does not radiate large amounts of light (Dark matter). This interesting result will keep popping up

throughout the rest of the course as we discuss the mass of the Universe.

Return to Lecture 2