Dynamical Tests

WEIGHING THE UNIVERSE

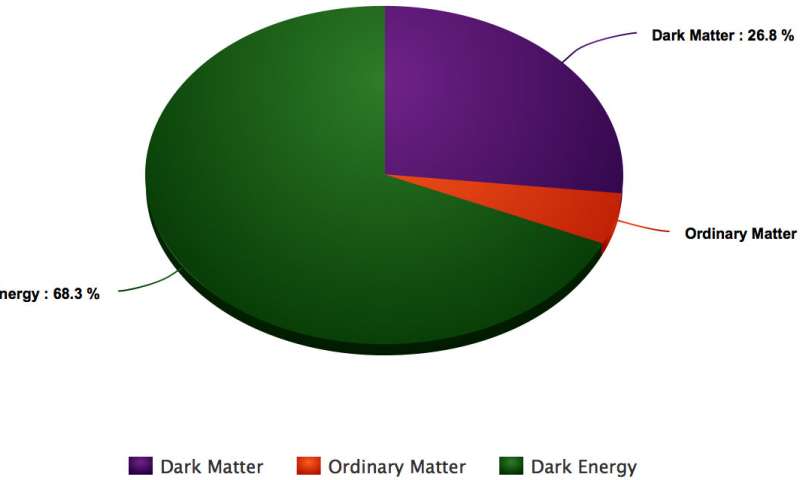
Before we go on, let's remind ourselves of the current composition of the Universe. We will deal with how much stuff that there is in the Universe. Not shown are the photons which make up much less than 1 % of the Universe.

There are obvious contributions to the density of the Universe, e.g., planets, galaxies, ... , however, there are also other not so obvious contributions. We need

total mass density = baryons + neutrinos + photons + dark energy + ...

Using the above, we define

So the issue becomes what are all of these contributions to Ω?

Before we go on, photons are in there, but why? Aren't photons massless?

The neutrinos (ν) are problematic.

The dark energy is more problematic; it is difficul to measure the dark energy with small z observations, but we'll mention some ideas later.

We can figure out how much of the mass of the Universe is contained in galaxies and galaxy clusters. Define

OUR PLAN IS TO MEASURE Ωgalaxy

The above is a deep field image taken by the Hubble Space Telescope (HST) in which is shown vast numbers of galaxies. By current count it is estimated that the Universe contains around 2 trillion galaxies with, on average, each galaxy containing around 100 billion stars.

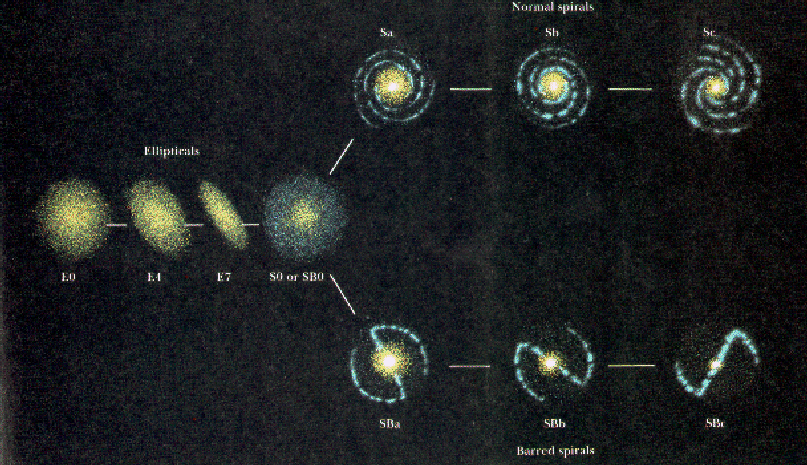
Galaxies are divided up into different types. There are Elliptical galaxies, and the disk-like galaxies which include Normal Spirals, Barred Spirals and Lenticulars which include normal S0s and barred SB0s . The galaxies were classified by Hubble forming his so-called Hubble Tuning Fork Diagram:

The different types of galaxies have different masses, and, in principle, we can find the mass in galaxies by adding the contributions from all galaxies in the Universe. Our galaxy, the Milky Way galaxy is classified as a barred Spiral galaxy with intermediately tightly wound spiral arms, in particular, we are an SBb galaxy. The SB stands for barred spiral and the b indicates the Milky Way has an intermediate sized bulge and mild winding for its spiral arms.

INDIVIDUAL GALAXIES

Dynamical methods are used to find galaxy masses (as already discussed). In dynamical methods, we rely on Newton's laws of motion and gravity. (Dynamical methods are applied on all scales -- from individual galaxies to pairs of galaxies to clusters of galaxies to clusters of clusters of galaxies and so on ... .)

Galaxy Rotation Curves (1970s)

Consider individual disk galaxies. We imagine that the stars and the gas in the disks of spiral galaxies orbit about the centers of the disk. In this case, gravity is balanced by the centrifugal force and we have that

M(galaxy) = Rv2/G

So, if we say, pick out a star and then measure how far it is from the center of the galaxy and how fast it is moving → mass contained within the orbit of the star (if the mass of the galaxy is distributed spherically). This is a powerful method, for example,

  • Measure rotation curves (Milky Way rotation curve) → R(Sun) ~ 25,000 light years ~ 2.5 x 1022 cm and V(Sun) ~ 220 km/s = 2.2 x 107 cm per second

    → M(Milky Way) ~ 1011 M(Sun) !

The Milky Way shows a flat rotation curve to large distances from its center. This is interesting because in our Solar System, the farther away from the Sun is a planet, the slower it moves in its orbit. This is easy to understand because the force of gravity weakens the further you are from the Sun.

    The fact that the orbital speed does not decrease indicates gravity does not weaken as quickly it does in our Solar System. This is naturally understood to mean that objects in our Galaxy have not yet moved out of the Milky Galaxy, we are still in the body of the Galaxy. The further out the rotation curve remains flat, the larger must be the Milky Way galaxy!

    Our galaxy has a thin disk of stars whose diameter is around 30,000 parsecs (100,000 light years) and thickness is 600 parsecs (2,000 light years). The disk is embedded in a large roughly spherical halo dominated by dark matter.

    The halo has a diameter of at least 100,000 parsecs based on the flat rotation curve of the Milky Way galaxy. It may be as large as 600,000 parsecs in diameter, which is just outrageous. The distance to Andromeda, M31 is around the same distance, that is, it is suggested that the Milky Way may stretch half-way to the Andromeda galaxy!

The Milky Way rotation curve is typical of other spiral galaxies. This is a nice way to measure the masses of galaxies in general ( rotation curves of some other galaxies.) The curves are all flat at large radii. Interestingly, when rotation curves are superimposed on pictures of the galaxies, we always see

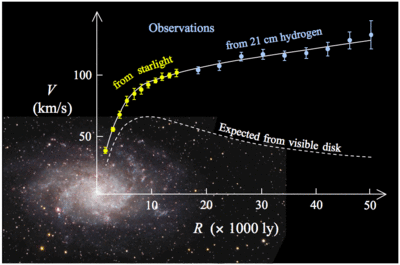
The above figure for the spiral galaxy M33 shows that the rotation curve is flat well outside the visible disk of the galaxy. This shows that there is unseen mass (Dark Matter) well outside the disk of stars in M33.

Dark Matter dominates Normal Matter (visible star stuff) in M33 (and other spiral galaxies).

Based upon studies of the rotation curves of many spiral galaxies, one is led to the same conclusion, the dark matter in the halos of the galaxies contributes at least 3 - 10 times the mass composing the luminous parts of the galaxies → Ω > 0.02 --> 0.07

CLUSTERS OF GALAXIES (1930s)

Coma Cluster

rich cluster with more than 1,000 galaxies, Radius ~ 3 Mpc, Distance ~ 99 Mpc

For one galaxy (roughly speaking), its motion is like orbital motion and we can infer the mass of the entire cluster of galaxies. Result:

M(total) ~ v2 {average R} / G → Ωcluster ~ 0.1 - 0.3

The method above gave the total mass of the galaxy cluster, but how does this compare to the ordinary visible mass? The ordinary matter radiates through starlight and also, because it is very hot, 10-30 million Kelvin, radiates in the x-ray as well. Below, we show images for the Coma cluster in the optical and in the x-ray.

The left hand image is an optical image of Coma taken by the Hubble Space Telescope. The right hand image is an x-ray image taken by Chandra X-ray Telescope. Note the triangular grouping in three galaxies near the center top in both figures. The optical light comes from the galaxies while the x-rays come from everywhere (actually from the gas in-between the galaxies). The optical emission and x-ray emission measure different pools of material. The hot x-ray emitting gas conatins 6 times the mass as tied up in the stars. However, the total amount of mass in the gas and stars is still only 1/10 of the total measured mass.

Dark Matter dominates the Visible Matter in clusters of galaxies

Peculiar Motions

The techinques about which I've talked, lead to Ω < 1. However, how did we get these values? Well, we had do some estimating. Because galaxies and clusters of galaxies are overdense regions of the Universe (much higher densities than the average universe), we needed to figure the size of boxes over which to average masses of the galaxies and clustes of galaxies.

It is apparent that on small scales the Universe is not isotropic and homogeneous, e.g., the Solar System is clearly lumpy. Thus, the question is On what scale does the Universe become smooth?, because it is on this scale and larger that we measure the average density of the Universe.

So far, the measurements of the mass (density) for the Universe have relied on galaxies and clusters of galaxies. Our measurements are thus local in that we measure the mass of the Universe where we can easily see mass. What are the consequences of this procedure?

If we start measuring the mass of the Universe on length scales greater than on the order of clusters of clusters of galaxies, then maybe we can start to feel fairly confident that we are actually measuring the average mass of the Universe.

MASS ESTIMATES BASED ON LARGE LENGTH SCALE ESTIMATES

Peculiar Velocities

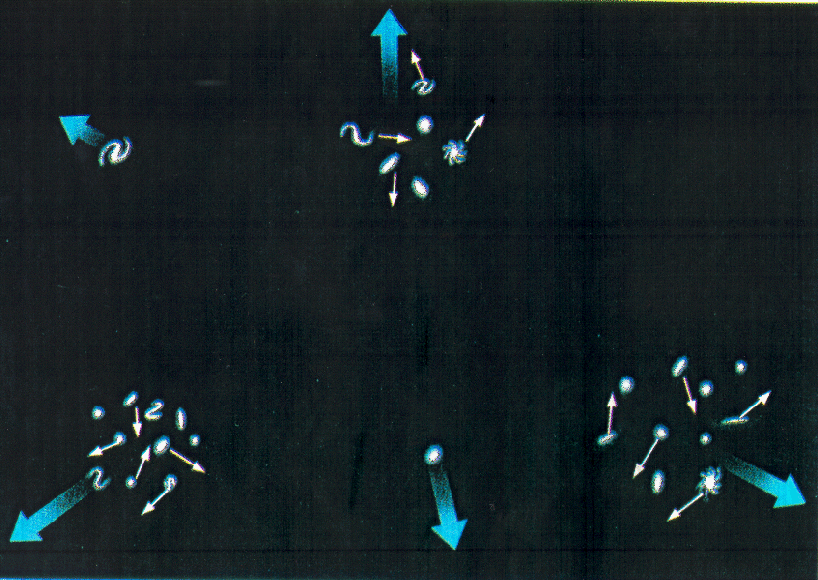
The overall Universe participates in the expansion, the Hubble flow, shown in the right panel. However, superimposed on the uniform expansion are smaller scale motions due to interactions between galaxies, clusters of galaxies, .... . These motions are referred to as peculiar velocities, streaming motions, ... . This is shown as the internal motions of the galaxies in the figure.

The significance of the peculiar velocities is that in order for them to have persisted over the lifetime of the Universe, they must be driven by something. If they were not being driven then they would have decayed away. The simplest explanation is that there are mass concentrations in the Universe which causes material to move around. For example, consider the

Anisotropy in the CMBR

Anisotropy is naturally interpreted as due to a peculiar velocity of the Milky Way galaxy. The motion has a speed of 600 kilometers per second in the direction of the Hydra-Centaurus supercluster on the sky.

Further (controversial) work showed that the Hydra-Centaurus cluster was also moving in the same direction at 800 kilometers per second and that more distant objects were actually approaching the same point. How did they know this? Well, consider the following Hubble plot. At d < D, the galaxies appear to have higher velocities than the Hubble relation. For d > D, the galaxies appear to have lower velocities than suggested by the Hubble relation.

How can we interpret this result? Well, imagine that there is a large mass concentration at D (the so-called, Great Attractor). This mass will then pull nearby objects toward it. So, things with d < D, will have enhanced velocities and objects with d > D will have decreased velocities compared to their Hubble flow values. More recent results have, however, shown that although we are pulled toward the Great Attractor, we, as well as the Great Attractor are also pulled toward the Shapley Supercluster. Our peculiar motion is thus driven by both the Great Attractor and the Shapley supercluster. This more recent result suggested that the Great Attractor's mass was less than originally estimated.

Results: G.A. at 130 Mly and M(GA) ~ 1016 M(Sun).

  • Estimates of Ωmass from Peculiar Velocities

    The peculiar velocities are due to mass concentrations which pull on things causing deviations from the Hubble flow. It is clear that the size of the perturbation (the size of the peculiar velocities) will depend upon how much mass pulls on the object. Results are uncertain but suggest that Ωmass may be as large as 1, but probably not.

    Gravitational Lenses

    Due to the curvature of space caused by concentrations of mass, light-rays bend as they pass by stars, galaxies, cluster of galaxies, ... . The bending makes masses act like lenses. A recent release from the HST of a lens produced by Abell 2218. The amount of bend is determined by the mass of the lensing object.

    Abell 1689 (shown to the left), lenses background objects. The HST's Advanced Camera for Surveys found that Abell 1689 lenses 34 different background objects. Redshifts provide distances for 24 of the objects. Using a model for Abell 1689, researchers matched the pictures to predictions made by models for the Universe that included our best guesses for how things work (see WMAP analysis of the CMB). Assuming a flat Universe and cold, dark matter, researchers found Ωmass ~0.3 and Ωdark energy ~ 1 with somewhat large uncertainties. They found at a 99 % confidence level, that the matter density is between 0.23 and 0.33, consistent with the WMAP results.

    Although uncertain, these observations suggest Ω = 1 (the Universe is flat) so that Dark Energy, Ωdark energy, dominates Matter, Ωdark energy+Ωbaryons, in the Universe.

    • IS DARK MATTER REAL?

    Up till now, dark matter and normal matter were only observed together (that is, they seemed to occupy the same spatial space). There was a suggestion that because of this, maybe dark matter was not actually real but the need for dark matter arose because there was something we did not understand about how gravity worked. It has then proposed that maybe we needed to modify gravity, and something called MOdified Newtonian Dynamics (MOND) was developed to explain all of the observed effects.

    BULLET Cluster. Two galaxy clusters collided. The gas content of the clusters (normal matter) shocked and heated up to millions of Kelvin and radiated x-rays, the reddish color in the image. The DARK MATTER interacting only weakly continued moving concentrating in the bluish regions to the right and left of the hot gas. This shows a clear separation between the Dark matter and the normal (baryonic) matter in the bullet cluster. This was important because previous observations were that the dark matter and normal matter occupied the same space which left open the possibilty that we simply didn't understand how gravity worked. The Bullet Cluster results strongly suggest that

    DARK MATTER is REAL

    Youtube video of Bullet cluster

    What is the Dark Matter?

    Due to the curvature of space caused by concentrations of mass, light-rays bend as they pass by stars, galaxies, cluster of galaxies, ... . The bending makes masses act like lenses.

    The above image is based on the gravitational lensing of objects behind the bullet cluster. The works shows where the mass is concentrated; it is clearly not where the x-rays are produced.

    Is our Dark Matter Halo Normal (baryonic) Matter?

    MAssive Compact HAlo Objects (MACHO), EROS, and OGLE. Experiments which viewed the Magellanic clouds to search for MACHOs in the galactic halo. Used gravitational lensing to search for MACHOs. Looked for stellar-like objects that did not radiate strongly, objects like small black holes, planets, rocks, and other compressed objects, not smoothly distributed particles.

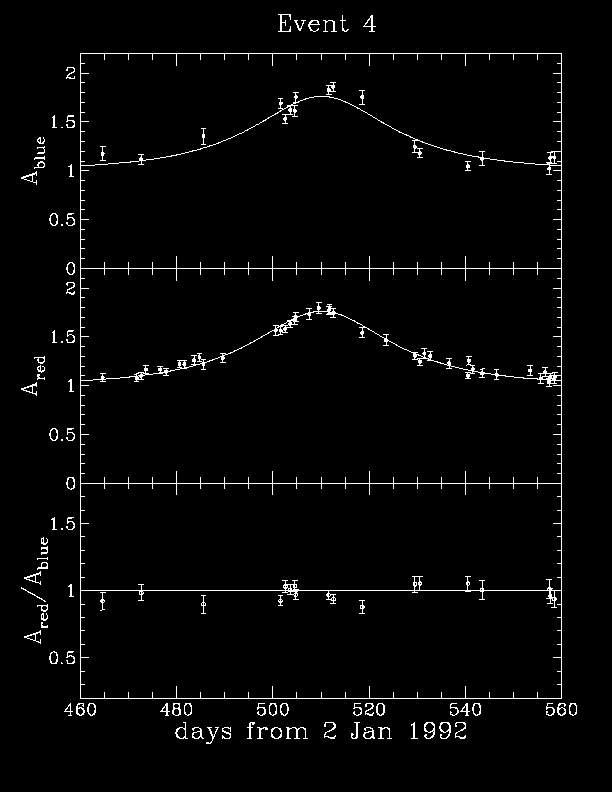
    MACHO, EROS, and OGLE each observed events, however, results were not consistent. MACHO found that perhaps 16 % of the halo were MACHOS, but OGLE and EROS were consistent with < 10-25 %, that is, consistent with 0 %. In any event,

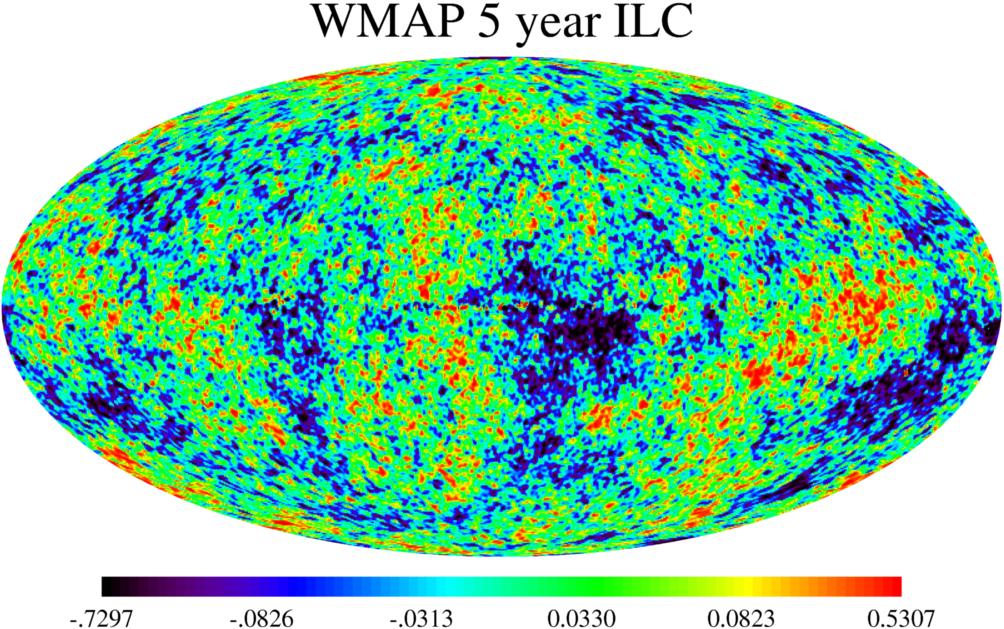
    MACHOs cannot explain all of the DARK MATTER

    →

    The fluctuations in the CMB at recombination eventually develop into the structure we see in the Universe today. The development of the structure is driven by gravity and may be modeled with a fair degree of confidence. We can thus pin down how large must be the fluctuations in the CMB. The fluctuations of the CMB have their origin much earlier in the Universe's history and are for the most part are DARK MATTER fluctuations. Modeling suggests that the properties of the DARK MATTER must be that they are

    Weakly Interacting Massive Particles (WIMPS) and cold (CDM), they move at speeds much slower than the speed of light.

    We know how DARK MATTER behaves, the trick is to find a particle which exhibits these properties. The search is an active research field in particle physics involoving theorists as well as experimentalists at the largest acclerators in the world, for example, the LHC at CERN, the European accelerator laboratory,

    Return to the Expansion of the Universe