Annual Trigonometric Parallax

---

Annual Trigonometric Parallax was first proposed by the ancient Greeks as a test of the helio-centric theory for the Solar System. They did not detect Annual Trigonometric Parallax and so assumed that the Solar System was earth-centered, geo-centric. Their result was correct in that they were unable to detect parallax because of limitations in technology. It was until 1838 that Bessel actually detected an annual trigonometric parallax.

---

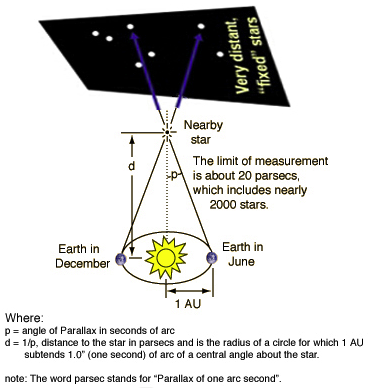
So, how large are expected parallaxes? Our nearest neihbor star, proxima Centauri, has distance 4.3 light years. This leads to a parallax angle of

angle = 1 Astronomical Unit / 4.3 light years = 0.0002^o

This is a tiny angle. We invent a new measure of angles to better describe parallax angles. Divide 1 degree into 60 parts (60 arc minutes) and then further divide 1 arc minute into 60 parts (60 arc seconds). This means that we divide 1 degree into 3,600 arc seconds.

---

The distance to proxima Centauri has a parallax angle of about 0.7 arc second. By the way, this is where the somewhat arcane unit of 1 parsec (1 parallax second) comes from. A parsec is the distance a star would have if it had a parallax angle of 1 arc second.

---

From Earth the best we can do is accuracies of around 0.01 arc seconds limiting our view to rather close to the Earth around 100 light years from Earth. The game changer came with the launches of the Hipparcos satellite in 1989 and the Gaia satellite in 2013. The Gaia satellite can measure parallax angles so small that distances to stars within 30,000 light years from Earth can be measured. Gaia measures parallax angles as small as 0.00002 arcsecond (20 microarcseconds).

---