The Masses of the Sun and Stars |

|
The Masses of the Sun and Stars |

|
The most reliable way in which to determine the masses of celestial objects is to study objects which are in binary systems. For example, the mass of the Sun can be determined by studying the motion of the Earth about the Sun; the Earth does not fall into the Sun because of its orbital motion. The gravitational pull of the Sun is counteracted by the centrifugal force generated by the orbital motion of the Earth. The stronger the pull of gravity, the faster the Earth must move in order to keep from falling into the Sun. This is illustrated by the figure to the right (modeled after one found in Newton's Principia). Imagine a cannon fired from a mountaintop. As the cannonball moves around the Earth, the Earth pulls it downward. However, as it falls downward, the ground, simultaneously, falls away from it. If the cannonball falls at the same rate as the ground falls away, then the cannonball never hits the ground and the cannonball orbits the Earth. |

|
Because the pull of the Sun's gravity depends upon its mass and how far we are away from the Sun (the A.U.), we can use the speed of the Earth to infer the mass of the Sun. Formally, we use Newton's formulation of Kepler's Third Law of Planetary Motion, i.e.,
where P is the orbital period of the planet, π = 3.14, a is the semi-major axis of the planet's orbit and G is the gravitational constant. The semi-major axis a is the average of the closest and fartheset approach of the stars about the center-of-mass of the system, where the center-of-mass is defined below,
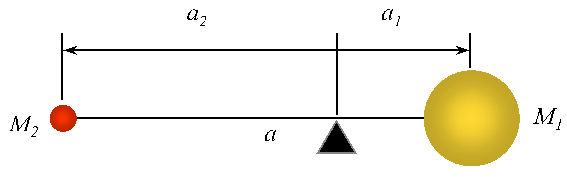 .
.
This method is also used to determine the masses of nearby binary stars.