We determine the temperatures of stars from an analysis of their light (spectra). Spectral analysis is an important topic and so we will spend a fair amount of time on it. We will consider:

• how stellar spectra are formed
• how stellar spectra are used to infer the surface temperatures of stars
• how stellar spectra are used to give the chemical compositions of the atmospheres of stars

Both the continuous and absorption line spectra of stars can be used to infer the surface temperatures of stars. To understand continuous vs. line spectra, consider the spectrum of the Sun (left panel).

If a more efficient tool is used to break up the Solar radiation into its constituent colors, we would, for example, see a continuous plus complicated line spectrum (right panel). The above plot shows how bright (how much power is carried by the photons) the Sun is at particular wavelengths (spectrum). The peak brightness shows at which wavelength (color) the star appears brightest. More on this below.

---

Continuous Spectrum and Temperature

Blackbody Radiation

The continous part (the smooth part) of the spectrum of most stars resembles the spectrum of idealized radiators known as blackbodies. Blackbodies are materials which are perfect absorbers of energy. Material such as soot are very black and nearly blackbody in character. However, interestingly, it may be the Universe itself which forms the most perfect blackbody we have yet detected (The Cosmic Microwave Background radiation has a nearly perfect blackbody spectrum).

The emission spectrum of a blackobdy is easily calculated because of its simple nature. Their spectra are referred to as blackbody spectra or Planck curves. They are exceedingly simple in character; their emission is characterized by only their temperature T .^*Nothing else matters, their shapes, sizes, what they are made of, and so has no bearing on how they radiate! The extremley happy circumstance is that stars radiate in a manner which can roughly be described as blackbody. We use this fact, below and later.

(1) A simple measure of the temperature of a star is based on its color because we know from studies on blackbodies in Terrestrial laboratories and theoretical musings, that the spectra of blackbody radiators of different temperatures look like;


The higher the temperaure of a blackbody, the more radiate it radiates at all wavelengths but the bluer (the shorter the wavelngth) at which its peak emission falls. The color of a star (blackbody) is then determined by its temperature. Cooler stars produce relatively larger amounts of red light compared to blue light than do hotter stars.

(2) In addition to simply using the color of a star to infer its temperature, we can also use the information contained in Wien's law,

λ_max = 0.3 centimeters - Kelvin / T(K),

to infer temperatures of stars. In the above T(K) is the temperature as measured in Kelvin. The wavelength inferred from the Wien Law is in centimeters if the above expression is used. Wien's Law says that the wavelength at which a blackody radiator is the brightest is determined by the inverse of its temperature.

Below, we show the Solar spectrum. The Sun is indeed fairly well-represented by a blackbody spectrum:

In the above, the example blackbody shown has temperature T = 5,250 C + 273 C = 5,523 Kelvin.

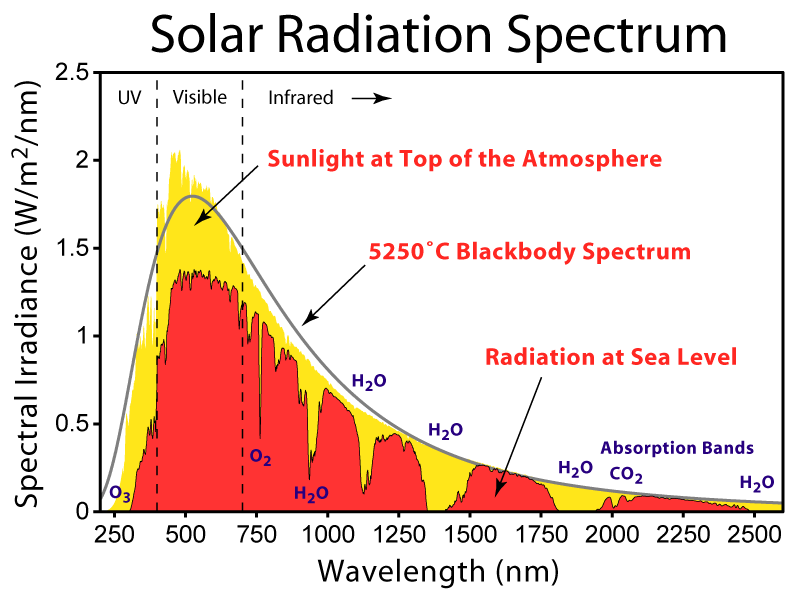
Let's estimate the temperature of the Sun using Wien's Law, λ = 0.3 cm-K / T(K). Looking at the spectrum we see that the Sun is the brightest at a wavelength of 5x10^-5 cm (see the above plot but note that the wavelengths are measured in nm = nano-meters = 10^-9 meters = 10^-7 cm). Then the temperature of the Sun is given by

T(K) = 0.3 cm-K / λ = 0.3 cm-K / 5x10^-5 cm = 6x10³ K

---

STEFAN-BOLTZMANN LAW Another property of a blackbody radiator is described by the Stefan-Boltzmann law. The Stefan-Boltzmann law tells us how much power a blackbody radiates per unit area of its surface. For a blackbody of temperature T, the power radiated per unit area (flux) is f = σ T4

---

Using the Stefan-Boltzmann Law we can understand why sunspots appear dark even though they are exceedingly hot, Sunspots have temperatures of 4,500 K. A comparison of the power radiated per unit area of a Sunspot and the surrounding surface of the Sun can be made using the Stefan-Boltzmann Law. We have (Brightness of Sun)/(Brightness of Sunspot) = (5,800 K/4,500 K)4 = 2.8 that is, the Sun is roughly 2.8 times as bright as a Sunspot.

---

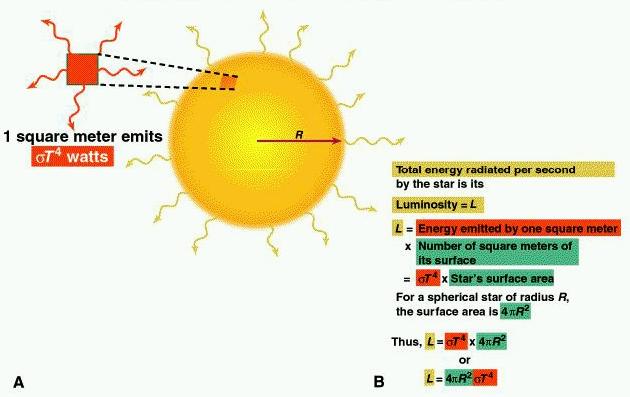
By itself, the Stefan-Boltzmann law is interesting but when used in conjunction with other known quantities, it can be used to infer properties of a star. For example, if a star radiates like a blackbody, then the luminosity of the star can be written as

L = (Surface Area of the Star) x (power per unit area produced by the star) = 4π R² σ T⁴

So, if we know certain information (obtained through independent means) about a star, we can infer other properties. For example,

• If we know the luminosity and temperature, we can infer the radius of the star;
• If we know the luminosity and radius of a star, we can infer its temperature;
• If we know the radius and temperature of a star, we can infer its luminosity

The point is, we cannot use the Stefan-Boltzmann law to infer properities of a star based on an observation, unless we have already certain (independently obtained) information in hand. It is not a way to directly measure properties of a star.

---