Atomic Physics

Atomic Physics

Atomic Physics

Based on the experiments of Bunsen and Kirchhoff, it was known that the wavelengths (energies) of the spectral lines for particular elements were the same every time they were measured and the patterns of the lines were unique to one element. The lines thus serve as fingerprints for atoms.

The element to which a given atom corresponds is defined by the number of protons it contains in its nucleus. The number of electrons and neutrons is irrelevant in terms of the determination of the type of chemical element.
The number of protons in an atom (nucleus) is given by the Z of the nucleus. We have

Element
Number of Protons in Nucleus, Z

hydrogen

1

helium

2

lithium

3

berylium

4

and so on

For the rest of the periodic table, see here.
So, how do the neutrons fit into this scheme? Whether an atom contains zero neutrons or many neutrons in its nucleus does not affect the type of element it is; it is the number of protons which determines the chemical element. The neutrons do affect the mass of the atom (its atomic weight, A). To set the jargon, consider hydrogen with Z = 1 (1 proton).

A hydrogen can have 0 neutrons, and its weight is A = Z + # of neutrons = Z = 1
A hydrogen can have 1 neutron, and its weight is then A = 2 (and is called deuterium).
A hydrogen can have 2 neutrons, and its weight is then A = 3 (and is called tritium). Tritium is highly radioactive (unstable).
All of the above are isotopes of hydrogen.
The mass of a proton is ~1,836 times that of an electron while neutrons and protons have roughly the same mass ===> the mass of an atom is contained in its nucleus while the nucleus is only

(1 fermi)³/(1 A)³ ===> 10^-15 of the volume of the atom.

Atoms are mostly empty space.
If we make an analogy with the Solar System, we can imagine that the nucleus is the Sun, and the electrons are the planets. The electrical force plays the role of gravity. This analogy is useful, however, there are important differences between how our Solar System works and how an atom works.

In our Solar System, the planets can, in principle, move about the Sun in orbits of any size.

In an atom, the electrons cannot orbit about the the nucleus in any old orbit. There is a set of well-defined orbits in which electrons can move ===> electrons can exist only with well-defined amounts of energy in an atom.

The above properties of atoms are not intuitive and it wasn't until the twentieth century when they were reasonably well-understood and could be modeled. The physics used to model these and other related phenomena is referred to as Quantum Mechanics. We will have more to say about Quantum Mechanics in the future. For now consider the following representation for the structure of an atom:

We will use the well-type picture to represent an atom.

Hydrogen

The hydrogen atom is particularly attractive to theorists because of its simplicity. Its most common form (isotope) contains one proton and one electron. Here are some facts about hydrogen atoms

The energy needed to strip an electron from the lowest level is 2.2x10^-18 Joules. This is a tiny number and so a different unit is used the electron volt. There are around 6x10¹⁸ electron volts in one Joule!! In terms of electron volts, the energy required to remove an electron from the bottom level of a hydorgen atom is 13.6 electron volts. (The process of removing an electron from an atom is known as ionization.)

The energy needed to strip electrons from higher levels in the well is easily found. Bohr showed that the energy needed was given by

Energy = 13.6 eV / n²

where n is the level. The lowest level is n = 1, the next higher level is n = 2, and so on.

electrons exist only in certain levels (energy states), an atom cannot absorb photons with arbitrary energies. Due to conservation of energy, an atom can only absorb an amount of energy which just promotes an electron to a higher level. (What does this say about the production of absorption and emission lines?) The energy of a photon capable of inducing a transition between levels n = 1 and n = 2 is

Energy = 13.6 eV/1¹- 13.6 eV/2² = 10.2 eV

Because the strength of the electrical force depends upon the charge of the nucleus (number of protons) and the number of electrons, different atoms have different energy structures.

Absorption and Emission of Photons

Note that the largest transitions (longest arrows) require the highest energy photons, particles of light, because the transitions have the largest changes in energy. The photons which produce the largest transitions therefore involve the photons with the shortest wavelengths (since E = hc/W = hf).

If an electron jumps to a higher energy level, it must absorb energy and this corresponds to an absorption line

If an electron drops to a lower energy level, it must get rid of energy and this corresponds to the production of a photon (an emission line is produced).

If the electron leaves the atom, the atom is ionized.
Comment: (i) A neutral atom is denoted by I. An atom which has lost 1 electron is denoted by II. An atom which has lost 2 electrons is denoted by III, and so on. For example, neutral hydrogen is HI; singly ionized hydrogen is HII.
Comment: (ii) To ionize an atom, all we require is that the photon have enough energy to lift the electron out of the well. If the photon has more than this threshold energy, it simply gives the excess energy to the electron (as kinetic energy). So, in terms of the appearance of the spectrum, we find that there is a threshold where ionization begins followed by a broad trough which extends to shorter wavelengths (higher energies). Such ionization edges are seen in the spectra of many stars.

If an electron is captured by an atom, we say that a recombination has taken place

Some definitions:

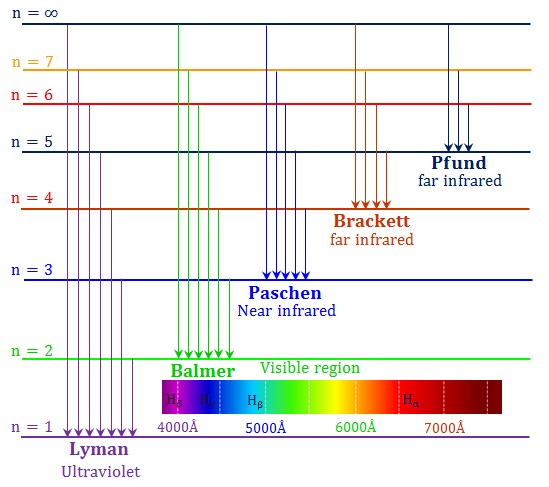
Lyman line: An electron starts from n = 1 and jumps to a higher level or an electron drops from a higher level to n = 1,
Balmer line: An electron starts from n = 2 and jumps to a higher level or an electron drops from a higher level to n = 2,
Paschen line: An electron starts from n = 3 and jumps to a higher level or an electron drops from a higher level to n = 3,
Brackett line: An electron starts from n = 4 and jumps to a higher level or an electron drops from a higher level to n = 4,
Pfund line: An electron starts from n = 5 and jumps to a higher level or an electron drops from a higher level to n = 5,

Lyman lines fall in the ultraviolet. Balmer lines fall in the optical. Paschen, Brackett, and Pfund lines fall in the infrared.