Tying Things Together: Hertzsprung-Russell Diagram, Mass-Luminosity Relation, Mass-Radius Relation, Luminosity Function

Hertzsprung-Russell Diagram

We know masses, radii, luminosities, surface temperatures, colors, distances, spectra, ... of many stars.
Question: How do we make sense of the plethora of available data?

The first step is to graph the data. The reason we go through this exercise is because plots can indicate whether properties of different stars are correlated, that is, if there is seems to be a physical relationship (connection) between the different properties.

H-R Diagram
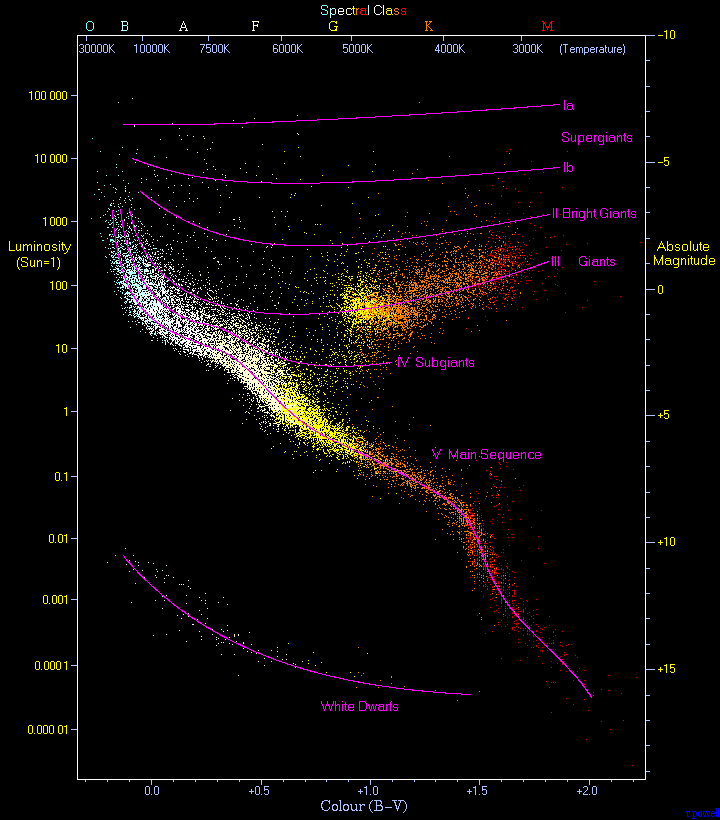
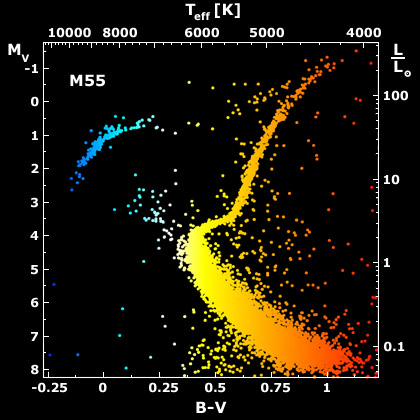
In the early 1900's, Ejnar Herstzprung and Henry Norris Russell independently made the discovery that the luminosity of a star is related to its surface temperature. The resulting plot is amazing. A Hertzsprung-Russell diagram (compiled primarily from Hipparcos data) is shown to the right. A Hertzsprung-Russell diagram for the old cluster M55 (Mochejska & Kaluzny, see APOD, 2001 Feb 23) is the top panel on this page. The Hertzsprung-Russell (HR) diagram was one of the most important astronomical discoveries of the twentieth century.
Hertzsprung and Russell used the spectral class (which is related to the surface temperature and color of the star [which is related to B-V]) and the magnitude in the V band (or B band) in their plots. They ordered the stars as O, B, A, F, G, K, and M. Since O stars are the hottest stars, this means that the temperature axis in the HR diagram is odd in that the temperature decreases as one moves to the right. The veritcal axis is the luminosity of the star, it increases upward. The axis is in magnitudes and so is logarithmic (mimicing the human eye).

Stars are confined to specific regions in the HR diagram. This tells you that there is some physical relationship between the luminosity and temperature of a star. To make this point clear, let's look at people. People have many defining characteristics, not all of which are related. What if we plotted some properties of people? Consider, a

plot of weight versus IQ. It will be a scatter diagram ===> there isn't a physical relationship between weight and IQ.

A plot of weight versus height for a sample of people shows a correlation ===> that there is something in the structure of people which makes weight and height correlated.

The simple exercise of plotting teaches us something about people. We did not learn in detail how people are put together but we did learn that the height and weight of people are somehow related. It is up to theorists to explain the how and why of the physical connection between the height and weight of the people population.
Similarly, the HR diagram is not telling us about how stars are put together. It is, again, up to the theorists to tell us what is going on. However, for now, let's ignore the role of the theorist and just examine the HR diagram to see what we can deduce about stars.

Some Inferences Based on the Hertzsprung-Russell Diagram

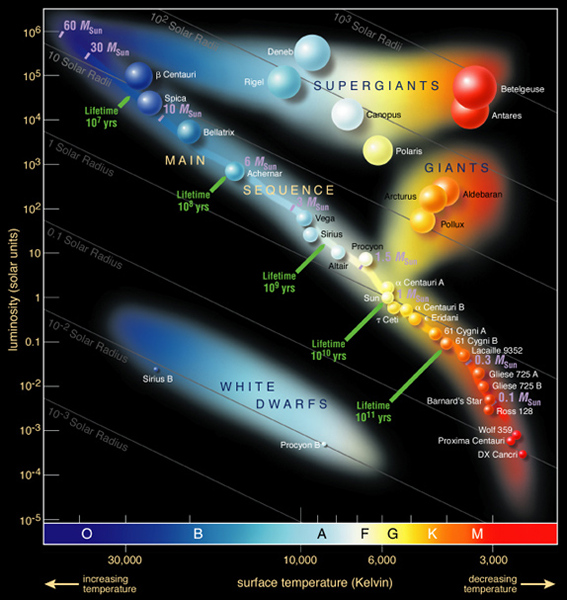
Luminosity Classes
I -- Super-Giants
II -- Bright Giants
III -- Normal Giants
IV -- Sub-Giants
V -- Main Sequence Stars

Question: What can we deduce from the HR diagram?

Address the names of the different groupings of stars, i.e.,, Main Sequence, Giants, Super-Giants,, and White Dwarfs. (By the way, these groups are also referred to as Luminosity Classes). Without having actually measured the radii of all of these stars, How did I know that the stars in the upper right hand corner of the diagram were big, while the stars in the lower left hand corner were small? (from Stefan-Blotzmann Law)

In a random sample of stars, roughly 85-90 % of the stars fall along the Main Sequence and the bulk of the other stars are White Dwarfs or Giants.

In a cluster of stars (e.g., M55), we see the following HR diagram:

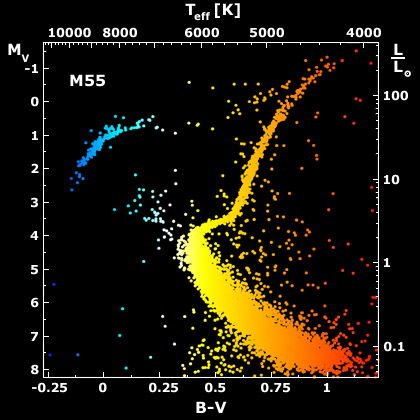
Question: What is this be telling us about stellar evolution?

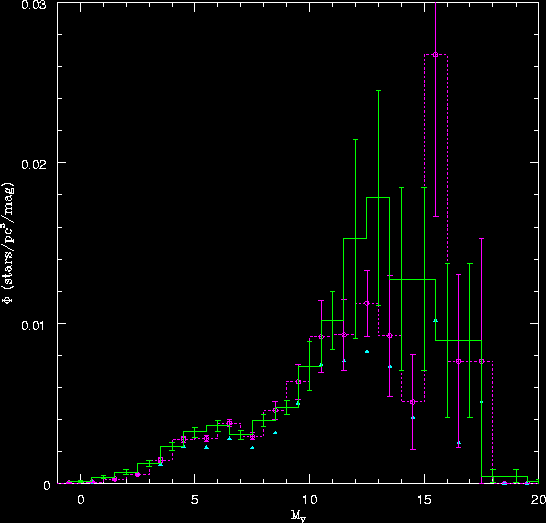
Luminosity Function
Even along the Main Sequence, stars are not distributed smoothly. There are many more low luminosity stars than there are high luminosity stars. A plot of this distribution is referred to as the Luminosity Function. The plot is for the Solar Neighborhood, but it is representative of stars in our Galaxy. Note that for stars the luminosity of our Sun, that there is around 1 stars every 1,000 cubic parsecs. That is, there is one Sun-like star in every cube whose sides are 10 pc long. Sun-like tars are roughly 10 parsec apart (30 light years) in the Solar Neighborhood. The number of stars increases strongly with decreasing luminosity. We find stars around 1 % the luminosity of the Sun, are separated by distances of around 1 parsec (3.3 light years).

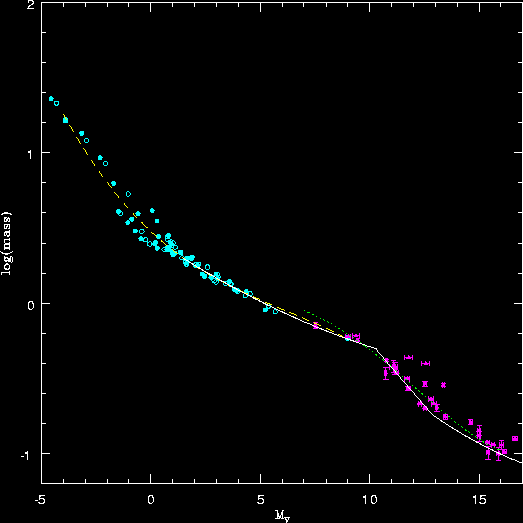Mass-Luminosity Relation for Main Sequence Stars
When we consider Main Sequence stars, is there any hint about whether an individual star evolves along the Main Sequence or whether a star once on the Main Sequence does not change its position? We believe that stars do not move along the Main Sequence. That is, Main Sequence stars with particular L have the same properties. This can be seen from the Mass-Luminosity relationship for Main Sequence stars.

Mass-Radius Relation for Main Sequence Stars
Radii of Main Sequence stars depend only weakly on mass. Although stars do not move along the Main Sequence, the mass-radius relation becomes uncertain because stars evolve even when on the Main Sqauence. We see this from the Mass-Radius relationship for Main Sequence stars.