512 | NATURE | VOL 534 | 23 JUNE 2016
LETTER
doi:10.1038/nature18322
The first gravitational-wave source from the isolated
evolution of two stars in the 40-100 solar mass range
1
,
2
,
1
&
3
The merger of two massive (about 30 solar masses) black holes
has been detected in gravitational waves
1
. This discovery validates
recent predictions
2–4
that massive binary black holes would
constitute the first detection. Previous calculations, however, have
not sampled the relevant binary-black-hole progenitors—massive,
low-metallicity binary stars—with sufficient accuracy nor included
sufficiently realistic physics to enable robust predictions to better
than several orders of magnitude
5–10
. Here we report high-precision
numerical simulations of the formation of binary black holes via the
evolution of isolated binary stars, providing a framework within
which to interpret the first gravitational-wave source, GW150914,
and to predict the properties of subsequent binary-black-hole
gravitational-wave events. Our models imply that these events
form in an environment in which the metallicity is less than ten
per cent of solar metallicity, and involve stars with initial masses
of 40–100 solar masses that interact through mass transfer and a
common-envelope phase. These progenitor stars probably formed
either about 2 billion years or, with a smaller probability, 11 billion
years after the Big Bang. Most binary black holes form without
supernova explosions, and their spins are nearly unchanged since
birth, but do not have to be parallel. The classical field formation of
binary black holes we propose, with low natal kicks (the velocity of
the black hole at birth) and restricted common-envelope evolution,
produces approximately 40 times more binary-black-holes mergers
than do dynamical formation channels involving globular clusters
11
;
our predicted detection rate of these mergers is comparable to that
from homogeneous evolution channels
12–15
. Our calculations
predict detections of about 1,000 black-hole mergers per year with
total masses of 20–80 solar masses once second-generation ground-
based gravitational-wave observatories reach full sensitivity.
We study the formation of coalescing black-hole binaries using
the StarTrack population synthesis code
16,17
. This method has been
updated to account for the formation of massive black-hole systems
in isolated stellar environments. The new key factors include an obser-
vationally supported star-formation rate, chemical enrichment across
cosmic time and a revised initial condition for evolution of binary stars.
Hitherto, simulations have been unable to achieve the desired predic-
tive power because of the limitations on the input physics (for example,
limited metallicity range) and numerical accuracy. To ensure the dom-
inant contribution from intrinsically rare low-metallicity star-forming
environments are adequately sampled, we use a dense grid of metallic-
ities (32 metallicities) with high precision (20 million binaries each).
Although binary population synthesis is dependent on a number of
uncertain physical factors, there has been recent progress in reducing
this uncertainty and understanding how it affects predictions. In light
of this, we consider the following three models to encompass major
sources of uncertainty (Methods): M1 represents our ‘standard’ classical
formation model for double compact objects composed of two black
holes (BH–BH), two neutron stars (NS–NS), or one of each (BH–NS);
M2 is our ‘optimistic’ model, in which Hertzsprung-gap stars may ini
-
tiate and survive common-envelope evolution, leading to many more
binaries being formed; and M3 is our ‘pessimistic’ model, in which
black holes receive large natal kicks, which disrupts and thereby reduces
the number of BH–BH progenitor binaries.
For each generated double compact object merger, with its intrin-
sic component masses and the redshift of the merger, we estimate
the probability that such a merger would have been detectable in the
first observing run (O1) of the Laser Interferometer Gravitational-
Wave Observatory (LIGO) advanced detectors. We adopt a self-
consistent model of evolution of stellar populations in the Universe
3,4
,
and we take the representative noise curve for O1 (https://dcc.ligo.
org/LIGO-G1501223/public) and assume 16days of coincident
science-quality observational time
1
.
In Fig. 1 we show the formation and evolution of a typical binary
system that result in a merger with similar masses and at a similar
time to GW150914. Stars that form such mergers are very massive
(40M
⊙
–100M
⊙
; M
⊙
is the mass of the Sun), and at the end of their
lives they collapse directly to form black holes
18
. Because there is no
associated supernova explosion, there is also no mass ejection. We
allow 10% of the collapsing stellar mass to be emitted in neutrinos.
If natal kicks are associated with asymmetric mass ejection (as in
our standard model), then our prediction is that these massive black
holes do not receive natal kicks and that their spin directions are the
same as that of their progenitor collapsing stars. The binary evolu-
tion removes the hydrogen-rich envelope from both binary compo-
nents, making both stars compact and luminous Wolf–Rayet stars
before they collapse to black holes. The first binary interaction is a
dynamically stable Roche-lobe overflow phase, whereas the second
interaction consists of a common-envelope phase that produces a
compact binary. After the common-envelope phase, the progeni
-
tor binary resembles two known high-mass X-ray binaries hosting
massive black holes: IC10X-1 and NGC300X-1 (ref. 19). A mas-
sive BH–BH binary (each with a mass of approximately 30M
⊙
) is
formed in approximately 5Myr of evolution, with a relatively wide
orbit (semi-major axis a ≈ 50R
⊙
; R
⊙
is the radius of the Sun), leading
to a long time to coalescence of t
merger
≈ 10Gyr. The accretion onto
the first black hole in the common-envelope phase is only modest
(approximately 1.5M
⊙
), whereas accretion from stellar wind of its
companion is rather small (less than 0.1M
⊙
).
To investigate general aspects of the formation history of GW150914,
we select a population of GW150914-like BH–BH mergers with a total
redshifted mass of M
tot,z
= 54M
⊙
–73M
⊙
, and then further restrict our
sample to binaries that would be detectable in O1. The formation
channels typical for these massive BH–BH mergers are summarized
in Extended Data Table 1.
We find that the most likely progenitor of GW150914 consists of a
primary star in the mass range 40M
⊙
–100M
⊙
and a secondary in the
mass range 40M
⊙
–80M
⊙
. In our standard model, the binary formed
1
Astronomical Observatory, Warsaw University, Ujazdowskie 4, 00-478 Warsaw, Poland.
2
Enrico Fermi Institute, Department of Physics, Department of Astronomy and Astrophysics, and Kavli
Institute for Cosmological Physics, University of Chicago, Chicago, Illinois 60637, USA.
3
Center for Computational Relativity and Gravitation, Rochester Institute of Technology, Rochester, New York
14623, USA.
© 2016 Macmillan Publishers Limited. All rights reserved
23 JUNE 2016 | VOL 534 | NATURE | 513
Let ter
reSeArCH
in a low-metallicity environment (Z < 0.1Z
⊙
; Z
⊙
is the metallicity of
the Sun; see Extended Data Fig. 1) and either in the early Universe
(2Gyr after the Big Bang) or very recently (11Gyr after the Big Bang).
The distribution of birth times of these massive BH–BH mergers is
bimodal (Fig. 2 and Extended Data Fig. 2), with a majority of systems
originating from the distant past (55% of binaries; about 2Gyr after
the Big Bang, corresponding to z ≈ 3) and a smaller contribution from
relatively young binaries (25%; formed about 11Gyr after the Big Bang,
corresponding to z ≈ 0.2). This bimodality arises from two naturally
competing effects: on the one hand, most low-metallicity star formation
occurs in the early Universe; on the other hand, in contrast to previous
work
3,4
, significantly more low-metallicity star formation is currently
expected to occur in the low-redshift Universe
20
. Therefore, as is the case
with binary neutron stars, we anticipate a significant contribution to
the present-day binary-black-hole merger rate from binary black holes
formed in low-redshift, low-metallicity star-forming regions. The delay-
time distribution of BH–BH binaries in our simulations follows a 1/t
distribution. The birth times therefore naturally pile up at low redshifts
(z ≈ 0.1–0.3) and this gives rise to a low-z peak (Extended Data Fig. 2a).
However, the low-metallicity (Z < 0.1Z
⊙
) star formation responsible for
the production of massive BH–BH mergers peaks at a redshift of z ≈ 3
(Extended Data Fig. 2b). The convolution of these two effects produces
the bimodal birth-time distribution (Extended Data Fig. 2c).
These massive GW150914-like mergers consist of black holes with
comparable masses. The vast majority (99.8%) of mergers are found
with mass ratios in the range q = 0.7–1.0 (Extended Data Fig. 3), with
the mass ratio of GW150914 (
=.
−.
+.
q 082
021
016
) falling near the centre of
the expected region. The formation of low-mass-ratio objects is sup-
pressed because low-mass-ratio progenitors tend to merge during the
first mass-transfer event when the more massive component overfills
its Roche lobe
21
. However, with decreasing total merger mass, the mass
ratio extends to lower values. In particular, for the lower mass bin of
M
tot,z
= 25M
⊙
–37M
⊙
, mass ratios as low as q = 0.3 are also found.
We now use our full sample of double compact object mergers to
make predictions for the merger-rate density, detection rates and
merger mass distribution. The results are shown in Fig. 3 and Extended
Data Table 1, in which we compare them to the measured values
inferred from O1 LIGO observations. We find an overall detection
rate that is consistent with the detection of one significant candidate
(GW150914) during the principal 16-day double coincident period
(when both LIGO gravitational-wave interferometers are operating
simultaneously) for our standard model (M1), but that is inconsistent
for our other two models (optimistic M2 and pessimistic M3; more
detail below).
The BH–BH merger rates inferred from the 16days of O1 LIGO
observations are in the range 2–400Gpc
−3
yr
−1
(ref. 22). For compar-
ison, we estimate the rate density of binary black holes from our popu-
lation synthesis dataset. We consider the full population of binary black
holes within a redshift of z = 0.1 (that is, not weighted by their detec-
tion probability) and calculate their average source-frame merger-
rate density. We find a value of 218Gpc
−3
yr
−1
for our standard model
(M1), which is in good agreement with the inferred LIGO rate
22
. By
contrast, our optimistic model (M2) predicts too many mergers, with
a rate density of 1,303Gpc
−3
yr
−1
, and our pessimistic model (M3)
Time (Myr)
0.0000
3.5445
3.5448
3.8354
3.8354
5.0445
5.0445
5.3483
5.3483
10,294
MS
HG
He star
BH
BH
BH
BH
BH
96.2M
գ
92.2M
գ
42.3M
գ
39.0M
գ
35.1M
գ
35.1M
գ
36.5M
գ
36.5M
գ
36.5M
գ
a (R
գ
) e
60.2M
գ
59.9M
գ
84.9M
գ
84.7M
գ
84.7M
գ
82.2M
գ
36.8M
գ
34.2M
գ
30.8M
գ
2,463
2,140
3,112
3,579
3,700
3,780
43.8
45.3
47.8
0
0.15
0.00
0.00
0.00
0.03
0.03
0.00
0.00
0.05
0.00
MS
MS
MS
MS
MS
CHeB
He star
He star
BH
Roche-lobe overflow
Zero-age main sequence
Direct collapse
Direct collapse
Merger
HG
or
CHeB
Common envelope
Figure 1 | Example binary evolution leading
to a BH–BH merger similar to GW150914.
A massive binary star (96M
⊙
(blue) + 60M
⊙
(purple)) is formed in the distant past (2 billion
years after Big Bang; z ≈ 3.2; top row), and after
5 million years of evolution forms a BH–BH
system (37M
⊙
+ 31M
⊙
; second-last row). For the
ensuing 10.3 billion years, this BH–BH system
is subject to loss of angular momentum, with
the orbital separation steadily decreasing, until
the black holes coalesce at redshift z = 0.09.
This example binary formed in a low-metallicity
environment (Z = 0.03Z
⊙
). MS, main-sequence
star; HG, Hertzsprung-gap star; CHeB,
core-helium-burning star; BH, black hole;
a, orbital semi-major axis; e, eccentricity.
© 2016 Macmillan Publishers Limited. All rights reserved
514 | NATURE | VOL 534 | 23 JUNE 2016
Let ter
reSeArCH
is at the very bottom end of the allowable range with a predicted rate
of 6.6Gpc
−3
yr
−1
. In our models, the BH–BH merger-rate density
increases with redshift (Extended Data Fig. 4). This increase is modest;
our predicted source-frame BH–BH merger-rate density would double
if the cut-off redshift was increased from z = 0.1 to z = 0.6.
The merger-rate density for the model with an optimistic
common-envelope phase (M2) is an order of magnitude larger than
the rate estimate from LIGO. This implies that unevolved massive stars
(during main sequence and Hertzsprung gap) do not initiate/survive
the common-envelope phase
9,23
. In our classical BH–BH formation
scheme, only evolved stars (during core helium burning) with well-
developed convective envelopes are allowed to initiate and survive the
common-envelope phase.
Our predictions for the pessimistic model (M3) imply that large natal
kicks (with average magnitudes of more than about 400kms
−1
) are
unlikely for massive black holes. This model predicts that an event such
as GW150914 would happen only 1% of the time, with the detection
of any BH–BH system happening less than 10% of the time (Table 1).
In principle, this conclusion applies to the formation of only the first
black hole in the binary, because large natal kicks lead to disruption of
BH–BH progenitors while the binaries are wide. During the formation
of the second black hole, the progenitor binaries are on very close orbits
(Fig. 1) and are not disrupted by natal kicks. In Extended Data Fig. 4 we
show a sequence of models with intermediate black-hole natal kicks;
future observations may allow us to discriminate between these models
and to constrain the natal-kick distribution. Future observations con
-
verging on M1 would indicate no natal kicks nor supernova explosions
in massive black-hole formation
18
. A striking ramification of this is the
prediction that hot and luminous Wolf–Rayet progenitors of massive
black holes
24
should disappear from the sky as a result of direct collapse
to a black hole (that is, with no supernova explosion). Targeted observa-
tional campaigns to search for such phenomena are already underway
25
.
Figure 3 shows the relative contribution to the overall merger-rate den-
sity associated with each bin of total redshifted merger mass M
tot,z
. For
comparison, Fig. 3 also shows the fiducial sensitivity (see Methods) as
a function of mass, assuming equal-mass zero-spin binary black holes.
Figure 3 demonstrates that the intersection of the strongly mass- dependent
sensitivity and the intrinsic detectable mass distribution strongly favours
sources with total redshifted masses of 25M
⊙
–73M
⊙
, consistent with
recent work
4
and total redshifted mass of GW150914 (M
tot,z
= 70.5M
⊙
).
In our simulations, the maximum intrinsic mass of a merging BH–BH
binary is M
tot
= 140M
⊙
. When accounting for cosmological redshift
0246810 12 14
0
0.5
1.0
1.5
2.0
2.5
Cosmic time (Gyr)
dR
det
/dt
birth
(yr
–1
(0.1 Gyr)
–1
)
Birth times of
massive BH–BH progenitors
Merger
Birth
Redshift
00.10.51.02.015
Figure 2 | Birth times of GW150914-like progenitors across cosmic time.
dR
det
/dt represents the contribution to the detection rate from binaries in a
given 0.1-Gyr bin of birth time. Half of the binaries that form BH–BH mergers
detectable in O1 with total redshifted mass in the range M
tot,z
= 54M
⊙
–73M
⊙
were born within 4.7Gyr of the Big Bang (corresponding to z > 1.2). The
birth and merger times of the binary depicted in Fig. 1 are marked in blue;
this binary follows the most typical evolutionary channel for massive
BH–BH mergers (BHBH1 in Extended Data Table 1). The merger redshift of
GW150914 is z = 0.088. The bimodal shape of the distribution originates from
a combination of the BH–BH delay-time distribution and the low-metallicity
star-formation history (see Extended Data Fig. 2 for details).
020
10
3
10
2
10
1
10
0
10
–1
10
–2
10
3
10
2
10
1
10
0
10
–1
10
–2
40
Total redshifted binary mass (M
գ
)
Merger-rate density (Gpc
–3
yr
–1
)
60 80 100 120 140 160 180
Upper limits
ab
GW150914
LIGO
BH–BH
M2
M1
M3
Table 1 | Expected detection rate and number of detections
Model Merger type O1 detection rate (yr
−1
)
Number of detections in
16 days of O1
M1 All 63.18 2.770
NS–NS 0.052 0.002
BH–NS 0.231 0.010
BH–BH 62.90 2.758
GW150914 11.95 0.524
M2 All 476.1 20.87
NS–NS 0.191 0.008
BH–NS 0.796 0.035
BH–BH 475.1 20.83
GW150914 110.0 4.823
M3 All 1.985 0.087
NS–NS 0.039 0.002
BH–NS 0.014 0.001
BH–BH 1.932 0.085
GW150914 0.270 0.012
The first column indicates the model: standard (M1), optimistic common-envelope phase (M2),
and large black-hole kicks (M3). The third column lists the expected detection rate R
det
per unit
double coincident time (both LIGO detectors operating at appropriate sensitivity), for a network
comparable to O1, for different classes of mergers (indicated in the second column). The fourth
column shows R
det
T, where T = 16days is the analysis time relevant for the rate estimate for
GW150914 (ref. 22). Entries for merger type ‘GW150914’ are for the subpopulation of BH–BH
mergers with total redshifted mass in the range M
tot,z
= 54M
⊙
–73M
⊙
.
Figure 3 | Comparison of merger rates and masses with O1 LIGO
results. Results are shown for standard (M1; red solid lines), optimistic
common-envelope phase (M2; pink dash-dotted lines) and pessimistic
large black-hole kicks (M3; green/black solid/dash-dotted line) models.
a, Distribution of total redshifted binary mass. The merger-rate density of
GW150914 (70.5M
⊙
) is indicated by the blue square (with 90% confidence
interval in mass, and its vertical position arbitrary). The blue solid line
shows the fiducial estimate of the sensitivity (or upper limits) of the 16-day
O1 run. A comparison of the shapes of the blue and red lines suggests
that the most likely detections for M1 are BH–BH mergers with masses in
the range 25M
⊙
–73M
⊙
. NS–NS mergers (first bin) and BH–NS mergers
(next five bins) are well below the estimated sensitivity and thus detections
in O1 are not expected. The rate densities are in the detector rest frame.
b, Comparison of the LIGO estimate of the BH–BH merger rate with
our models. The LIGO value of 2–400Gpc
−3
yr
−1
(90% credible range)
compares well with our standard (M1) and large black-hole natal kicks (M3)
models. The rate densities are in the source rest frame. An updated version
of Fig. 3, including additional gravitational-wave detections as they occur,
can be found at http://www.syntheticuniverse.org/stvsgwo.html.
© 2016 Macmillan Publishers Limited. All rights reserved
23 JUNE 2016 | VOL 534 | NATURE | 515
Let ter
reSeArCH
(M
tot,z
= (1 + z)M
tot
) and taking into account the advanced O1 hori-
zon redshift for this most massive binary (z = 0.7), the highest possible
observed mass within O1 would be approximately 240M
⊙
.
Spin magnitudes and directions of merging black holes are poten-
tially measurable by LIGO
1
. The second-born black hole in a BH–BH
binary does not accrete mass, and its spin at merger is unchanged
from its spin at birth. The first-born black hole, on the other hand,
has a chance to accrete material from the stellar wind of the unevolved
companion or during common-envelope evolution. However, because
this is limited either by the very low efficiency of accretion from
stellar winds or by inefficient accretion during common-envelope
evolution
26,27
, the total accreted mass onto the first-born black hole
is expected to be rather small (about 1M
⊙
–2M
⊙
). This is insufficient
to significantly increase the spin, and thus the spin magnitude of the
first-born black hole at merger is within about 10% of its birth spin.
In our modelling, we assume that stars that are born in a binary have
their spins aligned with the angular-momentum vector of the binary.
If massive black holes do not receive natal kicks (for example, in our
standard model M1), then our prediction is that black-hole spins are
aligned during the final massive BH–BH merger. We note that our
standard model includes natal kicks and mass loss for low-mass black
holes (less than about 10M
⊙
), and therefore BH–BH binaries with one
or two low-mass black holes may show misalignment. Alternatively,
binaries could be born with misalignment and retain it, misalignment
could be caused by the third body or by interaction between the radia-
tive envelope and the convective core
28
, or misalignment could result
from a large natal kick on the second-born black hole. Several binaries
are reported with misaligned spins
29
. Therefore, spin alignment of
massive merging black holes suggests isolated field evolution, while
misaligned spins do not elucidate formation processes.
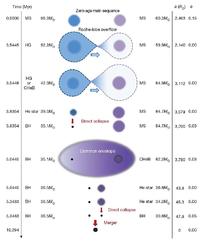
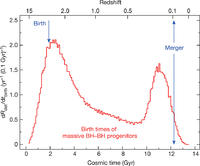
As shown in Fig. 1, we find that the formation of massive BH–BH
mergers is a natural consequence of isolated binary evolution. Our
standard model (M1) of BH–BH mergers fully accounts for the observed
merger-rate density and merger mass (Fig. 3), and for the mass ratio of two
merging black holes (Extended Data Fig. 3) inferred from GW150914.
Our standard formation mechanism (M1) produces significantly more
binary black holes than do alternative, dynamical channels associated
with globular clusters. A recent study
11
suggests globular clusters could
produce a typical merger rate of 5Gpc
−3
yr
−1
; our standard model (M1)
BH–BH merger-rate density is about 40 times larger: 218Gpc
−3
yr
−1
.
However, one non-classical isolated binary evolution channel involving
rapidly rotating stars (homogeneous evolution) in very close binaries
may also fully account for the formation of GW150914 (refs 12–15).
In particular, typical rates of 1.8 detections in 16days of O1 observations
are found
13
, which is comparable to our prediction of 2.8 (Table 1). Only
very massive BH–BH mergers with total intrinsic masses of more than
about 50M
⊙
are formed in this model
12,13
, whereas our model predicts
mergers with masses in a broader range, down to greater than about
10M
⊙
. Future LIGO observations of BH–BH mergers may allow us to
discriminate between these two very different mass distributions/models.
Online Content Methods, along with any additional Extended Data display items and
Source Data, are available in the online version of the paper; references unique to
these sections appear only in the online paper.
Received 21 February; accepted 11 May 2016.
1. Abbott, B. P. et al. Observation of gravitational waves from a binary black hole
merger. Phys. Rev. Lett. 116, 061102 (2016).
2. Belczynski, K. et al. The effect of metallicity on the detection prospects for
gravitational waves. Astrophys. J. 715, L138–L141 (2010).
3. Dominik, M. et al. Double compact objects. III. Gravitational-wave detection
rates. Astrophys. J. 806, 263 (2015).
4. Belczynski, K. et al. Compact binary merger rates: comparison with LIGO/Virgo
upper limits. Astrophys. J. 819, 108 (2016).
5. Tutukov, A. V. & Yungelson, L. R. The merger rate of neutron star and black hole
binaries. Mon. Not. R. Astron. Soc. 260, 675–678 (1993).
6. Lipunov, V. M., Postnov, K. A. & Prokhorov, M. E. Black holes and gravitational
waves: possibilities for simultaneous detection using first-generation laser
interferometers. Astron. Lett. 23, 492–497 (1997).
7. Nelemans, G., Yungelson, L. R. & Portegies Zwart, S. F. The gravitational wave
signal from the Galactic disk population of binaries containing two compact
objects. Astron. Astrophys. 375, 890–898 (2001).
8. Voss, R. & Tauris, T. M. Galactic distribution of merging neutron stars and black
holes – prospects for short gamma-ray burst progenitors and LIGO/VIRGO.
Mon. Not. R. Astron. Soc. 342, 1169–1184 (2003).
9. Belczynski, K., Taam, R. E., Kalogera, V., Rasio, F. A. & Bulik, T. On the rarity of
double black hole binaries: consequences for gravitational wave detection.
Astrophys. J. 662, 504–511 (2007).
10. Mennekens, N. & Vanbeveren, D. Massive double compact object mergers:
gravitational wave sources and r-process element production sites. Astron.
Astrophys. 564, A134 (2014).
11. Rodriguez, C. L., Chatterjee, S. & Rasio, F. A. Binary black hole mergers from
globular clusters: masses, merger rates, and the impact of stellar evolution.
Phys. Rev. D 93, 084029 (2016).
12. Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M. & Moriya, T. J. A new
route towards merging massive black holes. Astron. Astrophys. 588, A50
(2016).
13. de Mink, S. E. & Mandel, I. The chemically homogeneous evolutionary channel
for binary black hole mergers: rates and properties of gravitational-wave
events detectable by advanced LIGO. Mon. Not. R. Astron. Soc. http://dx.doi.
org/10.1093/mnras/stw1219 (2016).
14. Eldridge, J. J. & Stanway, E. R. BPASS predictions for Binary Black-Hole
Mergers. Preprint at http://arxiv.org/abs/1602.03790 (2016).
15. Woosley, S. E. The progenitor of GW150914. Preprint at http://arXiv.org/
abs/1603.00511 (2016).
16. Belczynski, K., Kalogera, V. & Bulik, T. A comprehensive study of binary
compact objects as gravitational wave sources: evolutionary channels, rates,
and physical properties. Astrophys. J. 572, 407–431 (2002).
17. Belczynski, K. et al. Compact object modeling with the StarTrack population
synthesis code. Astrophys. J. Suppl. Ser. 174, 223–260 (2008).
18. Fryer, C. L. et al. Compact remnant mass function: dependence on the
explosion mechanism and metallicity. Astrophys. J. 749, 91 (2012).
19. Bulik, T., Belczynski, K. & Prestwich, A. IC10X-1/NGC300X-1: the very
immediate progenitors of BH-BH binaries. Astrophys. J. 730, 140 (2011).
20. Hirschauer, A. S. et al. ALFALFA discovery of the most metal-poor gas-rich
galaxy known: AGC198691. Astrophys. J. 822, 108 (2016).
21. Bulik, T., Gondek-Rosinska, D. & Belczynski, K. Expected masses of merging
compact object binaries observed in gravitational waves. Mon. Not. R. Astron.
Soc. 352, 1372–1380 (2004).
22. Abbott, B. P. et al. The rate of binary black hole mergers inferred from
advanced LIGO observations surrounding GW150914. Preprint at
http://arxiv.org/abs/1602.03842 (2016).
23. Pavlovskii, K. & Ivanova, N. Mass transfer from giant donors. Mon. Not. R.
Astron. Soc. 449, 4415–4427 (2015).
24. Eldridge, J. J., Fraser, M., Smartt, S. J., Maund, J. R. & Crockett, R. M. The death
of massive stars – II. Observational constraints on the progenitors of Type Ibc
supernovae. Mon. Not. R. Astron. Soc. 436, 774–795 (2013).
25. Gerke, J. R., Kochanek, C. S. & Stanek, K. Z. The search for failed supernovae
with the Large Binocular Telescope: first candidates. Mon. Not. R. Astron. Soc.
450, 3289–3305 (2015).
26. Ricker, P. M. & Taam, R. E. The interaction of stellar objects within a common
envelope. Astrophys. J. 672, L41–L44 (2008).
27. MacLeod, M. & Ramirez-Ruiz, E. Asymmetric accretion flows within a common
envelope. Astrophys. J. 803, 41 (2015).
28. Rogers, T. M., Lin, D. N. C., McElwaine, J. N. & Lau, H. H. B. Internal gravity
waves in massive stars: angular momentum transport. Astrophys. J. 772, 21
(2013).
29. Albrecht, S. et al. The BANANA project. V. Misaligned and precessing stellar
rotation axes in CV Velorum. Astrophys. J. 785, 83 (2014).
Acknowledgements We are indebted to G. Wiktorowicz, W. Gladysz and
K. Piszczek for their help with population synthesis calculations, and to
H.-Y. Chen and Z. Doctor for their help with our LIGO/Virgo rate calculations. We
thank the thousands of Universe@home users that have provided their personal
computers for our simulations. We also thank the Hannover GW group for
letting us use their ATLAS supercomputer. K.B. acknowledges support from the
NCN grant Sonata Bis 2 (DEC-2012/07/E/ST9/01360). D.E.H. was supported
by NSF CAREER grant PHY-1151836. D.E.H. also acknowledges support from
the Kavli Institute for Cosmological Physics at the University of Chicago through
NSF grant PHY-1125897 as well as an endowment from the Kavli Foundation.
T.B. acknowledges support from the NCN grant Harmonia 6 (UMO-2014/14/M/
ST9/00707). R.O’S. was supported by NSF grant PHY-1505629.
Author Contributions All authors contributed to the analysis and writing of the
paper.
Author Information Reprints and permissions information is available at
www.nature.com/reprints. The authors declare no competing financial
interests. Readers are welcome to comment on the online version of the
paper. Correspondence and requests for materials should be addressed to
K.B. (chrisbelczynski@gmail.com).
Reviewer Information
Nature thanks M. Cantiello and the other anonymous
reviewer(s) for their contribution to the peer review of this work.
© 2016 Macmillan Publishers Limited. All rights reserved
Let ter
reSeArCH
METHODS
Our Monte Carlo evolutionary modelling is performed with the StarTrack binary
population synthesis code
16
. In particular, we incorporate a calibrated treatment
of tidal interactions in close binaries
17
, a physical measure of the common enve-
lope (CE) binding energy
30,31
, and a rapid-explosion supernova model that repro-
duces the observed mass gap between neutron stars and black holes (BHs)
18,32
. Our
updated mass spectrum of BHs shows a strong dependence on the metallicity of
the progenitor stars (Extended Data Fig. 5). In galaxies with metallicities similar to
the Milky Way (Z = Z
⊙
= 0.02), BHs that formed out of single massive stars (initial
mass M
ZAMS
= 150M
⊙
) reach a maximum mass of M
BH
= 15M
⊙
, whereas, for very
low metallicity (Z = 0.0001 = 0.005Z
⊙
), the maximum mass becomes M
BH
= 94M
⊙
.
The above input physics represents our standard model (M1), which is repre-
sentative of our classical formation scheme for double compact objects (BH–BH,
BH–NS and NS–NS).
We have adopted specific values for a number of evolutionary parame-
ters. Single stars are evolved with calibrated formulae based on detailed evolu-
tionary calculations
33
. Massive star winds are adopted from detailed studies
of radiation-driven mass loss
34
. For the Luminous Blue Variable phase, a high
rate of mass loss is adopted (1.5 × 10
−4
M
⊙
yr
−1
). Binary interactions and, in
particular, the stability of Roche-lobe overflow (RLOF) is judged on the basis
of binary parameters: mass ratio, evolutionary stage of donor, response to mass
loss, and behaviour of the orbital separation in response to mass transfer. The
orbital separation is additionally affected by gravitational radiation, magnetic
braking, and loss of angular momentum associated with systemic mass loss.
During stable RLOF, we assume that half of the mass is accreted onto the com-
panion, while the other half (1 − f
a
= 0.5) is lost with specific angular momentum
(dJ/dt = j
loss
[J
orb
/(M
don
+ M
acc
)](1−f
a
)dM
RLOF
/dt with scaling factor j
loss
= 1.0
where f
a
is the fraction of the mass accreted, J
orb
is the orbital angular momentum,
M
don
is the donor mass, M
acc
is the accretor mass, and dM
RLOF
/dt is the mass trans
-
fer rate; ref. 35). The CE is treated by considering the energy balance with fully
effective conversion of orbital energy into envelope ejection (conversion efficiency
α = 1.0), whereas the envelope binding energy for massive stars is calibrated by
a parameter λ, which depends on star radius, mass and metallicity. For massive
stars, λ ≈ 0.1 is adopted
31
. During CE evolution, compact objects accrete at 10%
of the Bondi–Hoyle rate as estimated by recent hydrodynamical simulations
26,27
.
Our CE evolution is instantaneous, so the time at the beginning and end of the
CE phase is exactly the same (see Fig. 1); the time duration of the CE phase has
no impact on our results.
We consider two extra variations of the input physics of binary evolution. In one
model (M2), we test highly uncertain CE physics
36
and we allow for Hertzsprung-
gap stars to initiate and survive CE evolution. This is an optimistic assumption,
because these stars may not allow for CE evolution
23
, nor survive as a binary if a
CE forms
9
. For comparison, in our standard model, we allow only evolved stars
with a deep convective envelope (core-helium-burning stars) to survive a CE phase.
In the opposite extreme, we use a model (M3) in which BHs receive large natal
kicks. In particular, each BH gets a natal kick with its components drawn from a
Maxwellian distribution with a one-dimensional root-mean-square σ = 265 km s
−1
,
independent of BH mass. Such large natal kicks are measured for Galactic pul-
sars
37
. This is a pessimistic assumption, because large natal kicks tend to disrupt
BH–BH progenitor binaries. This assumption is not yet excluded on the basis of
electromagnetic observations
4
. By contrast, in our standard model, BH natal kicks
decrease with BH mass. In particular, for massive BHs that form through direct
collapse of an entire star to a BH with no supernova explosion (M
BH
10M
⊙
for
Z = Z
⊙
, M
BH
15M
⊙
for Z = 0.1Z
⊙
and M
BH
15M
⊙
–30M
⊙
for Z = 0.01Z
⊙
), we
assume no natal kicks
18
. We also calculated a series of models with intermediate
BH kicks (see Extended Data Fig. 4): σ = 200 km s
−1
(model M4), σ = 130 km s
−1
(model M5) and σ = 70 km s
−1
(model M6).
For each evolutionary model we compute 2 × 10
7
massive binaries for each
point on a grid of 32 sub-models covering a wide range of metallicities: Z = 0.0001,
0.0002, 0.0003, 0.0004, 0.0005, 0.0006, 0.0007, 0.0008, 0.0009, 0.001, 0.0015, 0.002,
0.0025, 0.003, 0.0035, 0.004, 0.0045, 0.005, 0.0055, 0.006, 0.0065, 0.007, 0.0075,
0.008, 0.0085, 0.009, 0.0095, 0.01, 0.015, 0.02, 0.025 and 0.03. We assume that stellar
evolution at even lower metallicities proceeds in the same way as the evolution at
Z = 0.005Z
⊙
. However, stars with very low metal content (for example, Population
III) may evolve differently to metal-rich stars
38
.
Each sub-model is computed with initial distributions of orbital periods P
(proportional to [log(P)]
−0.5
), eccentricities e (proportional to e
−0.42
) and mass
ratios q (proportional to q
0
) appropriate for massive stars
39
. We adopt an initial
mass function that is close to flat for low-mass stars (proportional to M
−1.3
for
0.08M
⊙
≤ M < 0.5M
⊙
and to M
−2.2
for 0.5M
⊙
≤ M < 1.0M
⊙
) and that is top-heavy
for massive stars (proportional to M
−2.3
for 1.0M
⊙
≤ M ≤ 150M
⊙
), as guided by
recent observations
40
. The adopted initial mass function generates higher BH–BH
merger-rate densities as compared with the steeper initial mass function (propor-
tional to M
−2.7
for 1.0M
⊙
≤ M ≤ 150M
⊙
) adopted in previous studies
4,41
, because
there are more BH–BH merger progenitors in our simulations
42
.
A moderate binary fraction (f
bi
= 0.5) is adopted for stars with masses
M
ZAMS
< 10M
⊙
, whereas we assume that all more massive stars are formed in
binaries (f
bi
= 1.0), as indicated by recent empirical estimates
39,43
.
We adopt an extinction-corrected cosmic star-formation rate (SFR) based on
numerous multi-wavelength observations
44
:
⊙
()=.
(+)
+(+)/.
()
.
.
−−
z
z
z
MSFR0015
1
1[129]
Mpcyr
1
27
56
31
This SFR declines rapidly at high redshifts (z > 2). This may be contrasted with
some SFR models used previously
45
, which generated a greater number of stars
at high redshifts. This revision will thus reduce the BH–BH merger-rate densities
at all redshifts. Even though the formation of BH–BH binaries takes a very short
time (about 5Myr), the time to coalescence of two BHs may be very large (Fig. 1
and Extended Data Fig. 2).
In our treatment of chemical enrichment of the Universe, we follow the mean
metallicity increase with cosmic time (since Big Bang until present). The mean
metallicity as a function of redshift is:
∫
ρ
()=. +
(−).×(′)
(′)( +′)
′
Zz
yR z
HEzz
zlog[ ]05log
1978 10 SFR
1
d
z
mean
b
20
10
0
with a return fraction R = 0.27 (mass fraction of each generation of stars that is put
back into the interstellar medium), a net metal yield y = 0.019 (mass of new metal
created and ejected into the interstellar medium by each generation of stars
per unit mass locked in stars), a baryon density
⊙
ρ Ω=. ×
−
hM27710Mpc
b
11
b
0
2
3
with Ω
b
= 0.045 and h
0
= 0.7, a SFR given by Equation (1), and E(z) =
ΩΩΩ(+)+ (+)+
Λ
zz11
M
3
k
2
with Ω
Λ
= 0.7, Ω
M
= 0.3, Ω
k
= 0 and H
0
=
70.0 km s
−1
Mpc
−1
. The shape of the mean-metallicity dependence on redshift
follows recent estimates
44
, although the level was increased by 0.5dex to better fit
observational data
46
. At each redshift, we assume a log-normal distribution of
metallicity around the mean, with a standard deviation of σ = 0.5dex (ref. 47). Our
prescription (Extended Data Fig. 6) produces more low-metallicity stars than pre-
viously
41
. Because BH–BH formation is enhanced at low-metallicity
2
, our new
approach increases the predicted rate densities of BH–BH mergers.
Here we discuss caveats of evolutionary calculations. First, we consider only
isolated binary evolution, and thus our approach is applicable to field stars in
low-density environments. It is possible that dynamical interactions enhance
BH–BH merger formation in dense globular clusters
11
, offering a completely
independent channel.
Second, our predictions are based on a ‘classical’ theory of stellar and binary
evolution for the modelling of massive stars that we have compiled, developed
and calibrated over the last 15years. We do not consider exotic channels for the
formation of BH–BH mergers, such as the one from rapidly rotating stars in con-
tact binaries
48
.
Third, our modelling includes only three evolutionary models: a standard
model consisting of our best estimates for reasonable parameters (M1), as well as
optimistic (M2) and pessimistic (M3) alternative models. The optimistic model
consists of only one change from the standard model: we allow all stars beyond the
main sequence to survive the CE phase. Alternatively, the pessimistic model also
consists of only one change: larger BH natal kicks. We have not investigated other
possible deviations from the standard model (for example, different assumptions
of mass and angular-momentum loss during stable mass-transfer evolution) nor
have we checked inter-parameter degeneracies (for example, models with large BH
kicks and an optimistic CE phase). Precursor versions of these computationally
demanding studies have already been performed
49
, albeit with low statistics and
limited scope; these calculations indicate that our three models probably cover the
range of interesting effects.
Fourth, our observations are severely statistically limited. We are attempting to
draw inferences about our models on the basis of a single detection (GW150914).
In was argued
50
that the formation of GW150914 in isolated binary evolution
requires a metallicity lower than 0.5Z
⊙
. This argument was based on single stellar
models
51
; stars in close binaries are subject to significant mass loss during RLOF/
CE, and they form BHs with lower mass than BHs formed by single stars. Thus,
in binaries, the metallicity threshold for massive BH formation is lower than in
single stellar evolution. For example, formation of a single 30M
⊙
BH requires
Z < 0.25Z
⊙
(Extended Data Fig. 5, whereas formation of two such BHs in a binary
requires Z < 0.10Z
⊙
(Extended Data Fig. 1). The value of this threshold depends
on assumptions for the model of stellar evolution, winds and BH formation
© 2016 Macmillan Publishers Limited. All rights reserved
