Assignment 3
Age of the Universe and the Hubble Law
Due: 2017 May 1
Introduction
The Hubble Law is a fundamental piece of observational cosmology.
Here, we investigate how Hubble Law may be used to estimate
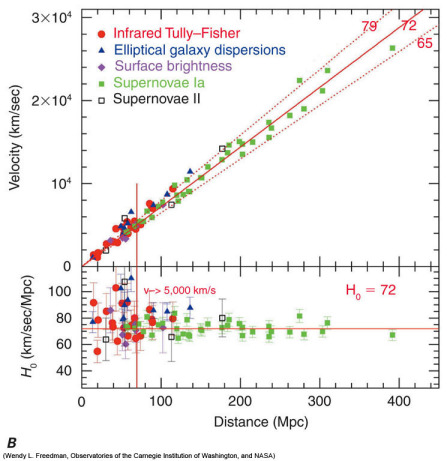
the age of our Universe. To the right is the Hubble Law determined
using several Standard Candles. The Hubble Law is the top panel,
the lower panel shows how well a straight line fits the observed galaxies.
Note that the best guess for the Hubble constant Ho is 72 km/sec
per Megaparsec or 22 km/sec per Million light years.
The distances are measured in Megaparsecs = 1 million parsecs = 3.2 million
light years = 3.1x1019 kilometers. The speeds are measured in units
of kilometers per second. |
 |
1. First, we will make a naive estimate for the
age of the Universe based on the Hubble
Law. The slope of the Hubble Law is
based on measurements made from the Earth, and
the Hubble constant quoted above
is the current best value for the expansion rate for
the Universe. Now, pick four galaxies on the plot, roughly
equi-spaced in distance interval from the Earth; choose one fairly
close to the Earth, another further away, a third one still further, and
a fourth at the largest distances. Draw circles
about each galaxy you have selected. Fill in the
following Table supplying the distances and velocities for the
galaxies you circled on the Hubble Law plot.
Be sure to convert values to the units indicated
in the Table. Use your chosen galaxies to infer
the age of the Universe, under the assumption
that at the birth of the Universe the Milky Way galaxy
and all other galaxies were sitting nearly on
top of each other.
When making your estimate for the age of
the Universe, assume that the rate of
expansion of the Universe has not changed over
the lifetime of the Universe.
Distance in Million parsecs (Mpc) |
Distance in kilometers
|
Speed in km/sec |
Expansion time
in seconds |
Expansion time
in years |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
2. What is the average age for the Universe based on the
data in your Table? How does your estimated
age compare to the currently accepted age of 13.7 billion years?
3. Sketch a plot of the scale factor R(t) for a Universe which has
expanded at a constant
rate (as per your assumption in Questions 1 and 2).
Next, suppose that the expansion rate of the Universe has been slowing
with time. Modify the portion of your plot of
the scale factor R(t) to show the expected changes.
Using this plot as guidance, surmise whether
your age estimate for the Universe
based on a constant expansion rate, is an overestimate or an
underestimate of the true of the Universe?

4. Indicate how your scale factor R(t) plot (in Question 3)
would change if the expansion rate of the
Universe was increasing as the Universe evolved.
For a universe whose
expansion rate increases with time,
is your age estimate an overestimate or an
underestimate?

