Assignment 2
Hubble Law
Due: August 19, 2010
Introduction
The Hubble Law is one of the fundamental pieces of observational evidence
upon which our modern theory (the Big Bang Theory)
of the structure and evolution of the Universe is built. Here, we investigate the
Hubble Law.
1. First determine the redshift of the objects.
 |
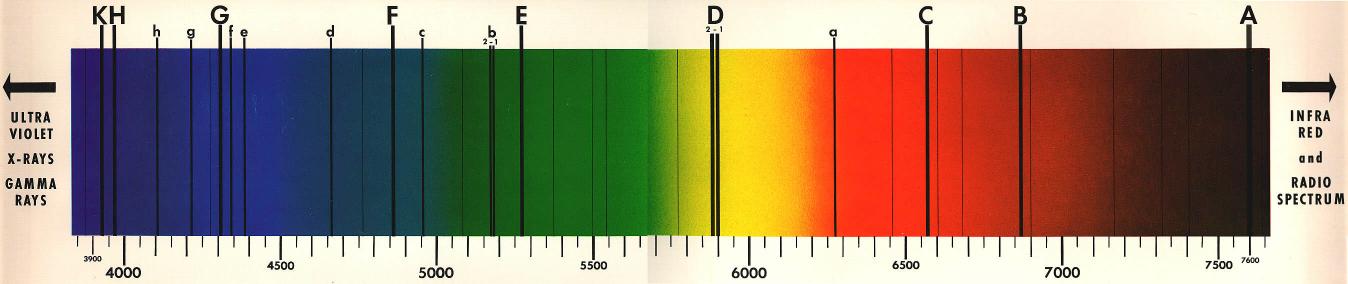
The above is a sample stellar spectrum. Because the light from galaxies (in the
visual part of the spectrum) is
roughly the sum of the light from billions of stars,
normal galactic spectra will resemble those of a set
of stars. For stars like the Sun,
the two lines produced by Calcium II (ionized calcium), known
as the
H and K lines, are very strong and are expected to appear
prominently in galactic spectra. The wavelengths of these two
lines are 0.3934 and 0.3968 microns (1 micron = 10-6 meters)
for K and H lines,
respectively. |
Get the redshifts for the following galaxy clusters
using the spectrum of the representative galaxy shown for each
cluster,
The observed K and H
lines are marked by the head of the arrow. The
location of the rest wavelength of the lines is marked
by the end of the arrow. The length of the arrow then gives
the change in the wavelength of the K and H
Ca II lines caused by the expansion of the Universe.
To calculate the redshift of each galaxy, first measure the
lengths of the arrows in centimeters. Next, note that the
positions marked by the letters a and e are
at wavelengths 0.3889 and 0.4472 microns so that points a
and e are separated by 0.4472 microns - 0.3889 microns
= 0.0583 microns. Use this information
to get the scale for the spectrum.
Using the lengths of the arrows and the scale for the
spectrum, find the change in wavelength of
the K and H Ca II lines in microns.
Fill in the
Change in K
and H wavelength, and Redshift
columns in the following Table. Recall that the
redshift z is given by
where the Greek letter lambda stands for wavelength. For the
rest wavelength, use the average of the Calcium II K and
H lines, 0.3951 microns.
Galaxy Cluster | Change in K and H wavelength | Redshift | Distance |
Virgo | | | 59,000,000 ly |
Ursa Major | | | |
Corona Borealis | | | |
Bootes | | | |
Hydra | | | |
2. We supplied the Distance to Virgo galaxy cluster
in the above Table. Under the assumption that all
galaxies have the same diameter, estimate the
distances to the other galaxies by comparing
how large they are in comparson to the size of M87 (the galaxy
shown for the Virgo cluster of galaxies).
Enter your estimates in the above Table.
3. Make a plot of the redshift versus distance
for the 5 galaxy clusters
using redshift as the vertical axis and Distance
for the horizontal axis. This plot forms Hubble's Law.
