 Nikolaus Copernicus |
Cosmological Principle |
 |
 Nikolaus Copernicus |
Cosmological Principle |
 |
We do not occupy a preferred place in the Universe (Copernican belief) and further, that at a given time, the Universe appears homogeneous and isotropic to all observers
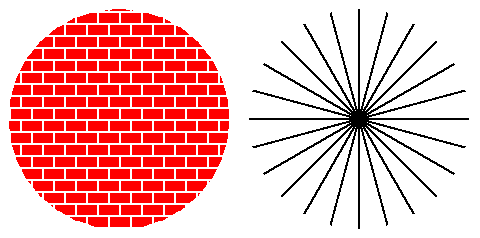 |
Homogeneous means that in some average sense, the Universe appears the same to all observers regardless of location. This is true for the left hand figure (the brick wall) but not for the right figure. Isotropic means that the Universe appears in all directions which one looks. If one is at the center of the figure on the right, this is true and so the Universe appears isotropic for an observer at the center of this Universe. The figure on the left does not appear isotropic for any observer! This remarkable suggestion is consistent with the smoothness of the CMBR, but more on this later. |
The question of the homogeneity and isotropy of the Universe cannot be answered until one specifies the size of the region which should be averaged over. For example, the Solar System is clearly inhomogeneous; there is a star at the center of the system which is surrounded by objects. The Solar System looks differently depending upon where you look. The scale upon which the Universe should appear homogeneous and isotropic is not well-defined, outside of the requirement that it is large (e.g., see Abell 2218 , Hubble Deep Field Photograph Great Wall),
There is structure in the Universe, but the argument is that it is small compared to the overall size of the Universe and so, in a sense, it can be averaged over ===> the Cosmologoical Principle is apparently valid.
The homogeneous and isotropic requirements are tough. Recall that the CMBR is homogeneous and isotropic but that regions in the Universe which are in opposite directions are not causally connected and so really have no reason why they should have the same properties. Why?
 |
|  |
|
 |
So, Why is the CMBR homogeneous and isotropic? This problem is known as the Horizon Problem.