|
World Views of the Universe
Reading: Chapter 26, Cosmology |

|
Cosmological Facts
- Expansion of the Universe
- Cosmic Microwave Background (CMBR)
- Hydrogen/Helium abundances
- mass of the Universe
- matter/anti-matter asymmetry
- large scale structure of the Universe
- Cosmological constant
- ....
The primary observational facts are the
first three results. The other results
will be discussed when appropriate. Before we move on to
the main topics, let us consider something known as
Olbers's Paradox
Models of the Universe
Based on Hubble's law and the CMBR, our world view of the Universe is rather
firm. On the assumption that Hubble's Law, v = Ho x D, is due
to an uniform expansion of the Universe, models have been constructed
based on Einstein's General Theory of Relativity
(GTR).
Einstein himself made models for the Universe (circa
1910-1920's). Unfortunately, he erred because he
believed in an homogeneous, isotropic, and
static Universe (on philosphical grounds).
- In a gravitating Universe, a static solution is not possible because
gravity is always attractive ---> it always tries to pull things closer
together
- To get around this problem, Einstein postulated the existence of a
large-scale repulsive force which could counteract gravity
- This force is parameterized by what is referred to as
The Cosmological Constant
(represented by the Greek letter capital
Lambda)
When Hubble's result became known (1929), Einstein immediately withdrew his
suggestion of a
Cosmological Constant as there was no need for
a large-scale repulsive force in a non-static Universe. Today,
however, the idea of a Cosmological Constant
has been revived. This does not
mean we believe in steady-state universes though; the basic models for the
Universe all consider models which are expanding. We will now consider the
properties of the proposed models.
Plan For Next 5 Weeks
I. I will first approach the Universe from a theoretical slant
II. I will next look at the observations relevant
to theory
III. Finally, I will consider our place in the Universe
I. Modern View of the Universe
After Einstein invented his General Theory of Relativity
, Alexander Friedman and Lemaitre developed
the first models for the (spacetime) structure
of universes based on Einstein's General Theory of
Relativity (GTR). (Lemaitre was the first to suggest that the
Universe came from an initial dense state, the
primeval atom and is therefore said to be
the father of the big bang, the term later coined by Fred Hoyle.)
Using GTR and assuming that
the Cosmological Principle
was valid for our Universe, Friedman found
three general types of universes,
flat, closed, and open each representing a different ultimate
fate for the Universe.

Sloan Great Wall |
Wait, recall that the Cosmological Principle
says that the Universe is homogeneous and isotropic for any observer
in the Universe. The appearance of the Universe can change with time, but
all observers must see the same Universe for any given time.
How is this consistent with the observed structure in
the Universe (structures more than 1 billion light years in size!)?
Despite the impressive sizes of these features
(e.g., the
Voids, and the Sloan Great Wall
--1.37 Billion light years across), these
structures are still less than 10 % of the distances to the farthest QSOs
(z ~ 6 ==> more than 25 billion light years away)
and thus fill less than 1 % of the volume of the Universe.
The Universe appears fairly bland on scales larger than these
observed features and the Cosmological Principle seems to hold for our
Universe.
|
To get a feel for Friedman's models, we demonstrate some properties of
Friedman universes using two-dimensional analogies.
Spacetime:
Recall that in order to determine the locations of
events in our Universe we must specify four things, the spatial location
(where)
and temporal location (when)
of the event ===> we must consider our
Universe to have four dimensions, the position and
time of an event. These define the spacetime coordinates of an event.
Note in our Universe although time is, in a sense, a simple coordinate
equivalent to position, time
occupies a preferred place in our
modeling in that we are not able to move arbitrarily in time
as we can through space.
|
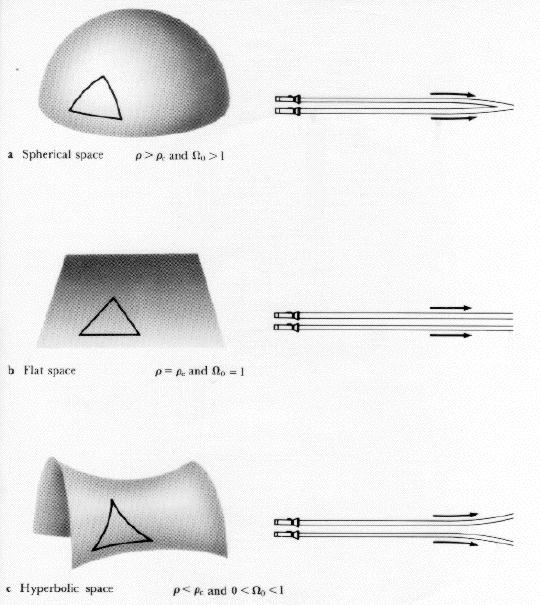
Interestingly, the framework upon which we
place these spacetime events
for the Universe can have different shapes and that the shape is
modified by the presence of mass (recall our discussion of black
holes, and singularities). In terms of spacetime, the Friedman models are
flat (Euclidean space, critical universe),
postive curvature (e.g.,
a sphere, the closed universe), and
negative curvature (e.g., a saddle, open universe)
universes. In two-dimensions, positive and negative cruvature spacetimes
look like
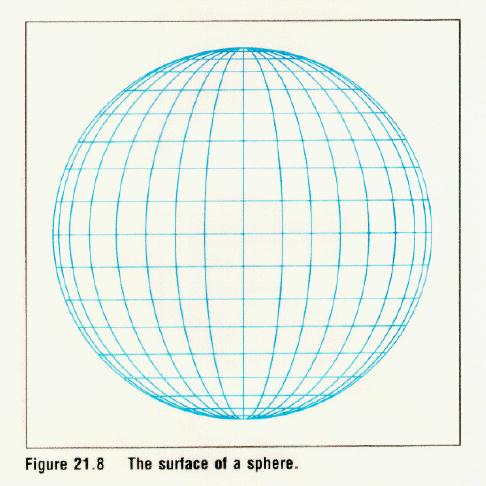
positive curvature |

negative curvature |
Abstract as these concepts are, these shapes
(topologies) have important consequences for how our Universe evolves;
the different shapes are indicative
of the ultimate fate of the Universe.
If we can determine the topology
(geometry or shape) of the Universe, we can infer what is going to
happen to our Universe
in the distant future. In the coming weeks, we will explore how astronomers
deduce the shape (topology) of our Universe and thus determine
the ultimate fate of our Universe.
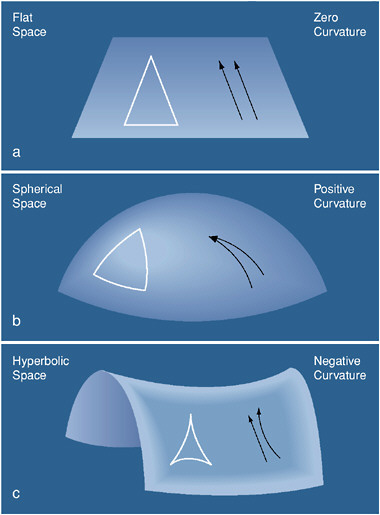
| Properties of Geometric Objects in Different
Universes
The geometry (curvature) of each type of universe is different; the
spacetime
of each universe has different character. A simple measurable difference
between the universes can be found from proprties of different geometric shapes
and features in each spacetime.
- Flat universes ---> expanding universe and will stop expanding after
an infinite amount of time; the flat universe is
the dividing line between open and
closed universes.
- Closed universes ---> expanding, but will reach a maximum size and
then collapse
- Open universes ---> expanding universe which will expand forever and
is infinite in spatial extent
|
Hubble Law and Topology of the Universe
How does the Hubble Law, that is, the relation between the redshift of
and distance to far-away galaxies behave and how is it interpreted
in the context of Einstein's GTR and the different Friedman models.
The different Friedman solutions affect the
Hubble Law at large distances primarily. |
|
Hubble's Law
In the context of Einstein's view of the universe,
How are Hubble's Law
and galactic redshifts interpreted?
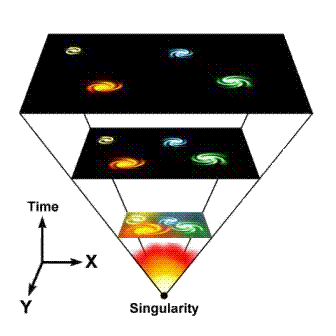
The galaxies and other denizens of the Universe are simply carried along by the
expansion of the spacetime.
In this sense, they may be stationary in the expanding
Universe; the apparent recession of distant galaxies with respect to our
home galaxy, the Milky Way, occurs because the distances of the
galaxies from us, grow with
time as the Universe grows in size! Each galaxy sees the other galaxies
behave in the same manner.
No one galaxy sits at the center of the universe,
furthermore, there is no center of the expansion. This difficult
conceptual point follows from the notion that the Universe itself is growing
in size, it is not expanding into anything and
so has no edges and therefore no center. All points in the Universe
are simply moving apart with time.
|
 |
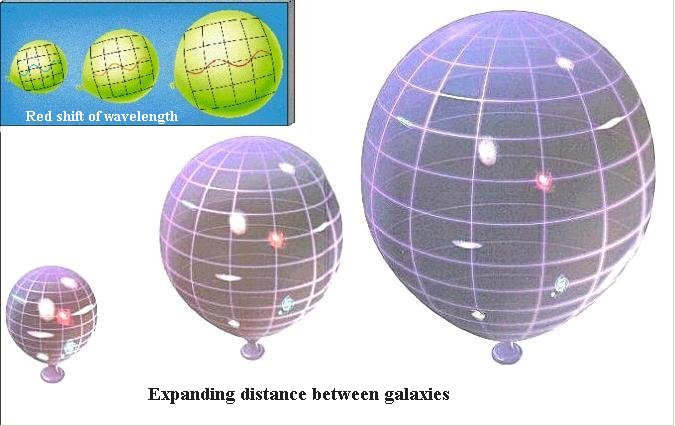
Cosmological Redshifts
Again, in an epxanding Universe, galaxies and the other denizens of the
Universe are carried along by the
expansion of the spacetime and, in this sense, are stationary. So,
How Do Galactic Redshifts Arise?
The apparent recession of distant galaxies with respect to our
home galaxy, the Milky Way, occurs because the distances of the
galaxies from us, grow with
time as the Universe grows in size! In addition, the light in the Universe
(see the inset to the right) also stretches as the Universe expands.
In this manner, the expansion of the Universe redshifts the light from distant
galaxies; the wavelength of the light when produced is smaller than today.
Such redshifts caused by the expansion of the
Universe are referred to as
Cosmological Redshifts
|
 |
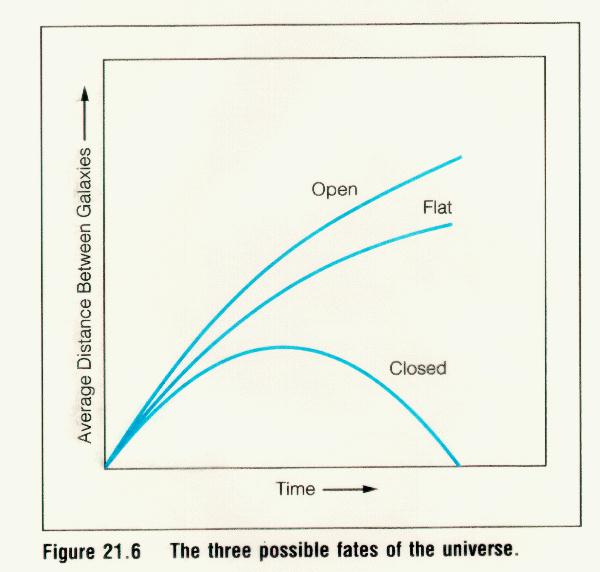
Scale Factor, R(t)
Properties of the different spacetime solutions can also be
readily visualized using what is referred to as
the scale factor
for the universe R(t). The scale factor, R(t),
tells us how much bigger or smaller the Universe is today than
it was yesterday and so on.
- Scale Factor ===> Size = R(t) x Size (in the past)
where Size (in the past) is usually the size of the universe at some point
in the past.
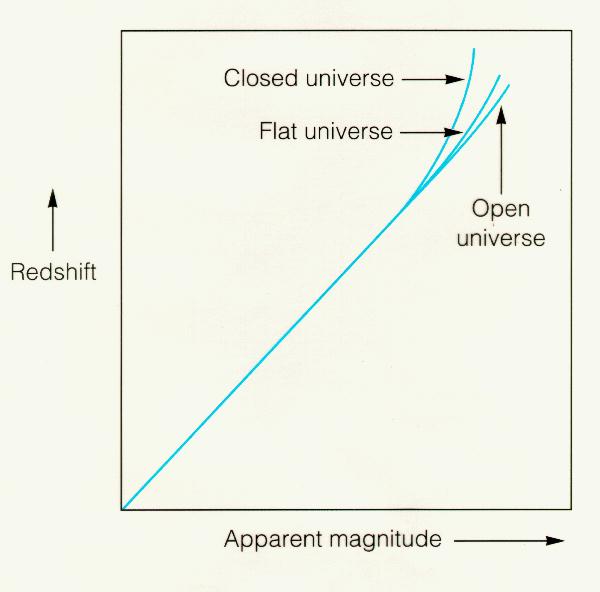
In terms of the scale factor R(t), the evolution of the three solutions
for the universe are shown to the right.
Closed universes correspond to the bottom curve.
Open universes correspond to the top curve.
Flat universes (critical universes) fall right between
closed and open universes.
|
|
A great deal of effort is now directed toward determining which of
the above models is the correct one for our Universe. The
methods used
to determine the correct universe model fall into three
categories:
- Dynamical Tests
where we check to see if the Universe exceeds
its escape speed by measuring the expansion rate of the Universe (the
Hubble constant, Ho) and the mass of the Universe
- Topological Tests
where we try and measure the shape
of the Universe
- Tests where we match
our most promising models to detailed observations of the Universe.
In particular, we see which model can best explain the snapshot
of the Universe taken at the Epoch of Recombination, that is,
through analysis of the Cosmic Microwave Background Radiation (CMBR).
We will spend a fair amount of time on these methods (later). Let me
first touch on some aspects of the second method. We consider results of
other more definitive tests later.
Topological Tests for the Shape of the Universe
In principle, if we sat down and drew large triangles and measured their
interior angles, we could determine the shape of the Universe. As a
practical matter this is difficult. The other geometric properties of the
Universe are also difficult to measure (as well). Are there other tests we
can apply? Yes.
 |
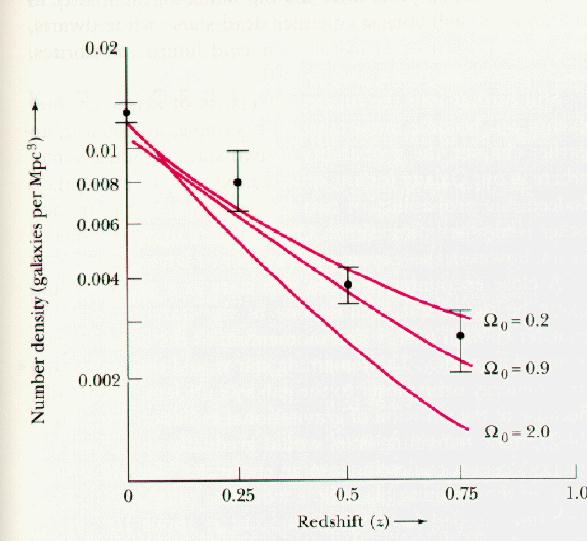
Angles, Areas, & Volumes
Depending upon the geometry of the Universe, the number density of galaxies
at large redshift (===>large distance) should
depend upon the geometry of the Universe. Why? Well, just as the
area of a circle depends upon the geometry of the Universe, the volumes of
objects may also depend upon the geometry of the Universe. The difference in
the way volumes depend upon distance will affect the way densities depend
upon distance. Tests for this effect have been carried out. The results
are interesting, but not conclusive.
|
 |
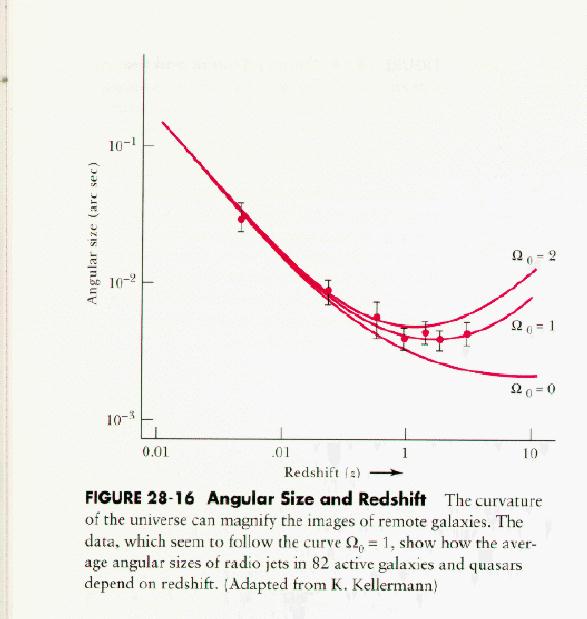
Parallel Lines
Depending upon the geometry of the Universe,
the paths of parallel lines can cross
or diverge, A consequence of this is that if
measures the angular sizes of distant
galaxies, they do necessarily have to decrease as 1/distance (as they
would in a flat universe). This effect has also also been studied. The
results are suggestive but, again, not conclusive.
|
Return to Home Page