CELESTIAL MOTIONS

Jimmy Imamura
Institute of Theoretical Science and Department of Physics
University of Oregon
March 3, 2010

Ancient Astronomers

Early astronomers were astrologers in that they were paid to watch the skies to chart periodicities and deduce other regularities in the motions of Celestial Objects. An interesting example of this are the Anasazi.
At left is shown a schematic of the sundagger at Fajada Butte in Chaco Canyon, the Solar Observatory of the Anasazi. To the right are photographs taken at the west site. Markings on double spiral near equinox. Top: September 30, 1984, 11:42.5 am (8 days after fall equinox). Middle: March 20, 1984, 11:48.5 am (9 hours after spring equinox). Bottom: March 23, 1984, 11:53.5 am (3 days after spring equinox). Photographs by Rolf Sinclair and Michael Marshall, copyright, The Solstice Project.

CONSTELLATIONS

Taurus the Bull

Ophiuchus the Snake Holder

Pisces the Fish

BASIC MOTIONS

Earth's rotation period, P = 23h56m4.091s

Earth's orbital period, P = 365.26 d

P(years) = a(Astronomical Units)³

CELESTIAL SPHERE AND THE MOTION OF CELESTIAL BODIES

Celestial Sphere, diurnal circles, and AAT site

Obliquity of Earth's rotation axis

Ecliptic (planets, Your Sky , check out the Grand Conjunctions of July 2060 and April 2002) ), Solstices, and Equinoxes

PRECESSION

Torque and Angular Momentum

Pole Wandering, Equinox Motion

FUNDAMENTAL FORCES IN THE UNIVERSE
There are only four known fundamental forces which govern all interactions in the Universe, the strong nuclear force, the weak nuclear force, the electromagnetic interaction, and gravity!!! This is truly astounding that something as large and seemingly complex as the Universe obeys only four fundamental notions of interaction. For the most part, distant Celestial objects interact only through the graviational force.

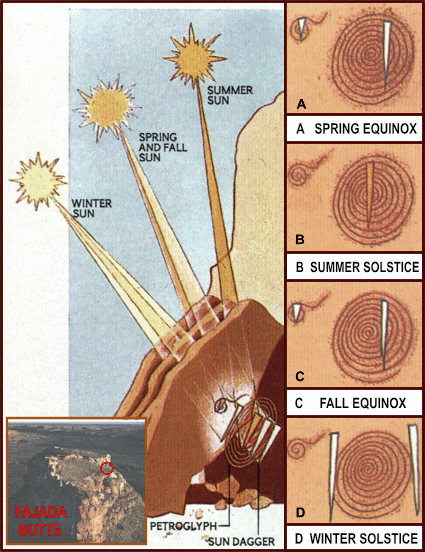
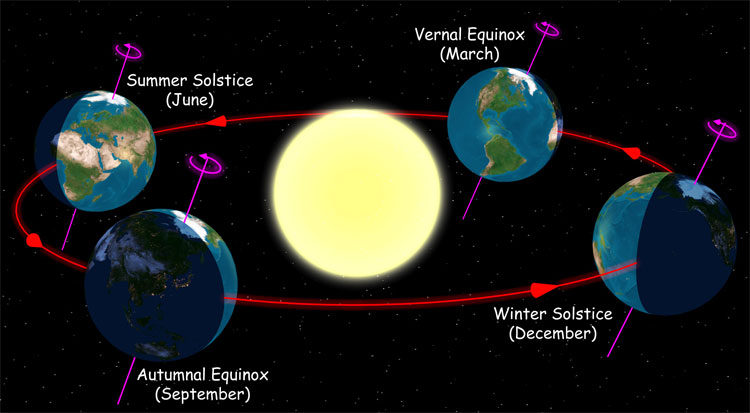
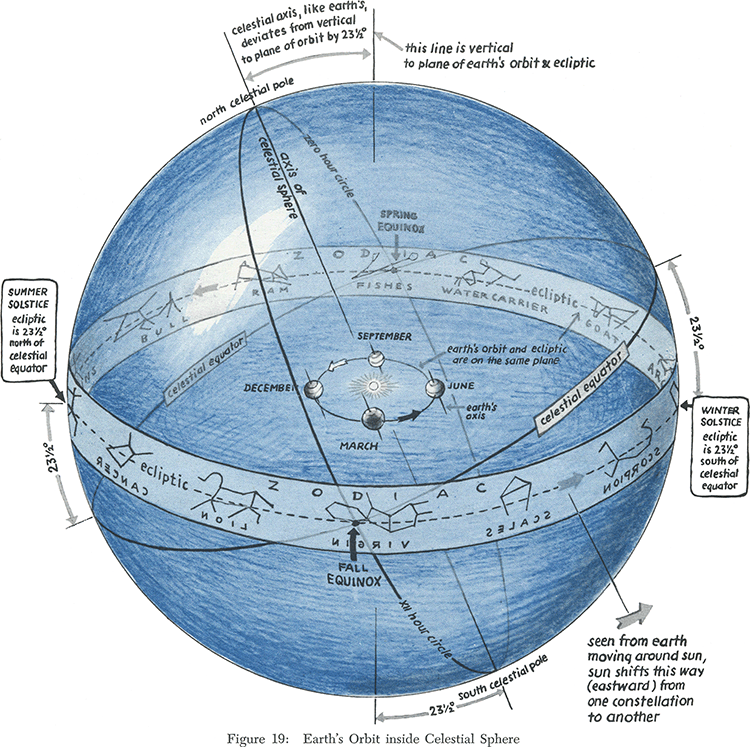
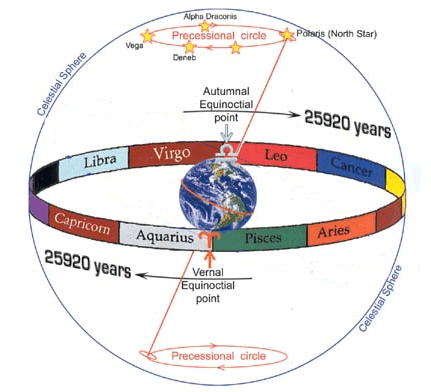
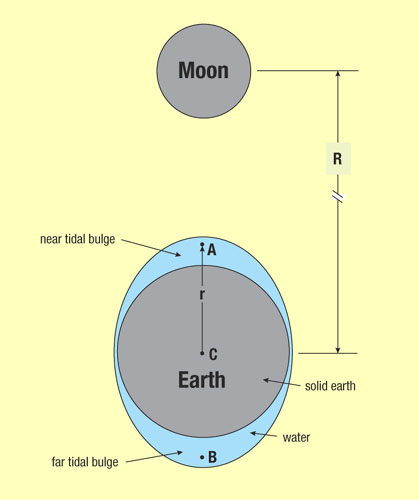
TIDAL FORCES
Tidal forces are differential forces. Let's consider how an object tidally distorts another object. The tidal force is the difference in force exerted on the object if one notes that the near side of the object is closer to the attractor than is the center of the object which, in turn, is closer than the far side of the attractor. Each part of the object feels a difference force. Tidal forces are the size the differences felt by masses at these differing positions in the object. For example, if we considered the tidal force exerted by the Earth on the Moon, we would find: 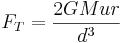where F_T is the tidal force, G is the gravitational constant, M is the mass of the distorting object, u is the mass of the object in question, r is the size of the object in question, and d is the distance between the distorter and the object in question.
Let's estimate the tidal force exerted by Jupiter on me and compare it to the tidal force exerted by a can of pepsi sitting on a table next to me. When comparing things, it is wise to take their ratio. We find F_J/F_pepsi = (M_J/D_J)³ /(M_pepsi/d_pepsi)³. The mass of Jupiter is M_J = 1.9x10²⁷ kilograms and at closest approach, Jupiter is around 600 million kilometers from the Earth. Now a 12 ounce can of pepsi has mass around 400 grams (0.4 kilograms) and, let' say it is around 1 meter from me. We find F_J/F_pepsi ~ 2.2x10^-8
Tidal forces are exceedingly weak.